已知椭圆(C:dfrac{x^2}{a^2}+dfrac{y^2}{b^2}=1) ((a>b>0))的左右焦点分别是(F_1,F_2),椭圆(C)的离心率为(dfrac{1}{2}),且椭圆(C)过点(left(1,-dfrac{3}{2}
ight)).
((1)) 求椭圆(C)的标准方程;
((2)) 若直线(l)过椭圆(C)的左顶点(M),且与椭圆(C)的另一个交点为(N),直线(NF_2)与椭圆(C)的另一个交点为(P),若(PF_1perp MN),求直线(l)的方程.
解析:
((1)) 由题易得关于(a,b)的方程组$$
dfrac{1}{a2}+dfrac{9}{4b2}=1,dfrac{b2}{a2}=dfrac{3}{4}.
[ 解得$left(a,b
ight)=left(2,sqrt{3}
ight)$.从而所求椭圆方程为$dfrac{x^2}{4}+dfrac{y^2}{3}=1$.
$(2)$ 由题,设$angle NF_2x= heta$,则由椭圆的焦半径公式$
m{II}$可得
$|NF_2|=dfrac{3}{2+cos heta}$,从而<p style="text-align:center;">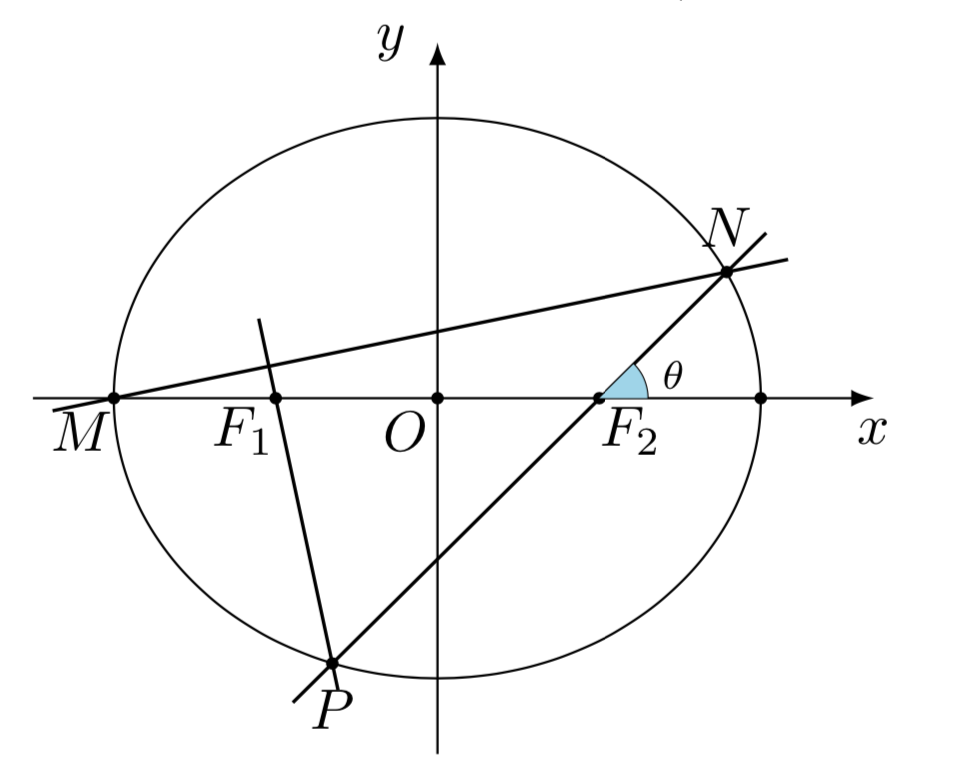</p>可得$N$点的坐标$Nleft(dfrac{3cos heta}{2+cos heta}+1,dfrac{3sin heta}{2+cos heta}
ight)$,同理可得$P$点坐标$Pleft(dfrac{-3cos heta}{2-cos heta}+1,dfrac{-3sin heta}{2-cos heta}
ight)$,由于$$PF_1perp MN Rightarrow
overrightarrow{PF_1}cdot overrightarrow{MN}=0.]
整理可得关于$ heta$的方程$$
(7cos heta-5)left(cos heta+1
ight)=0.$$
由于$M,N$两点不重合,因此$cos heta+1
eq 0$,从而当且仅当$cos heta=dfrac{5}{7}$对应的直线$l$即为所求.且该直线方程为$$
l: sqrt{6}x-12y+2sqrt{6}=0.$$