已知函数(f(x)=(ax+{ln}x)cdot(x-{ln}x)-x^2)有三个不同的零点(x_1,x_2,x_3) (()其中(x_1<x_2<x_3)),则(left(1-dfrac{{ln}x_1}{x_1}
ight)^2left(1-dfrac{{ln}x_2}{x_2}
ight)left(1-dfrac{{ln}x_3}{x_3}
ight))的值为((qquad))
(mathrm{A}. 1-a) (qquad mathrm{B}.a-1) (qquad mathrm{C}.-1) (qquad mathrm{D}.1)
若记$$t(x)=dfrac{{ln}x}{x},x>0.$$则(t)的取值范围为(left(-infty,dfrac{1}{mathrm{e}}
ight]),则由(f(x)=0)可得关于(t)的一元二次方程$$
t^2=(1-a)(t-1),tleqslant dfrac{1}{mathrm{e}}.$$如下图绘制出二次函数(y=t^2,tleqslant dfrac{1}{mathrm{e}})与(y=(1-a)(t-1))的图象,若要使得(f(x))有三个不同的零点,
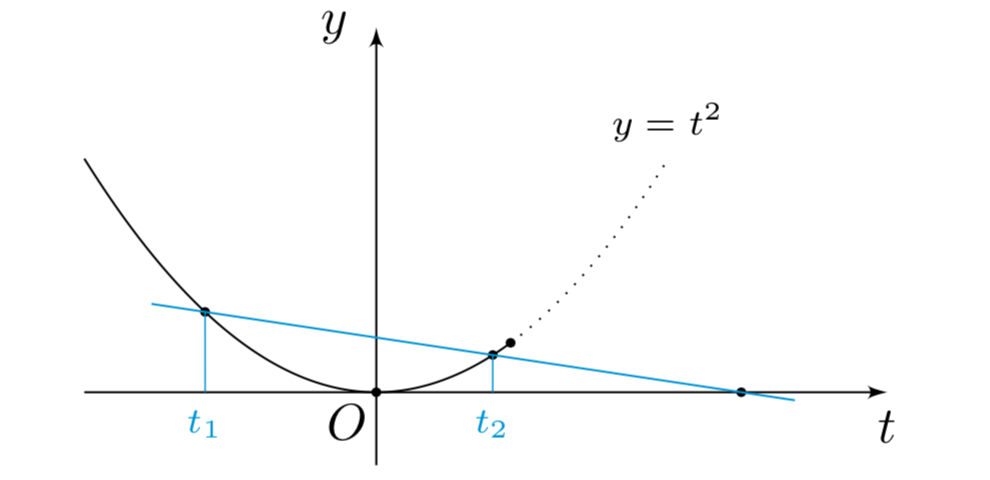
t_1<0<t_2,t_1+t_2=1-a,t_1t_2=1-a.$$再结合(t(x)=dfrac{{ln}x}{x})的图象,可知$$t_1=t(x_1),t_2=t(x_2)=t(x_3).$$
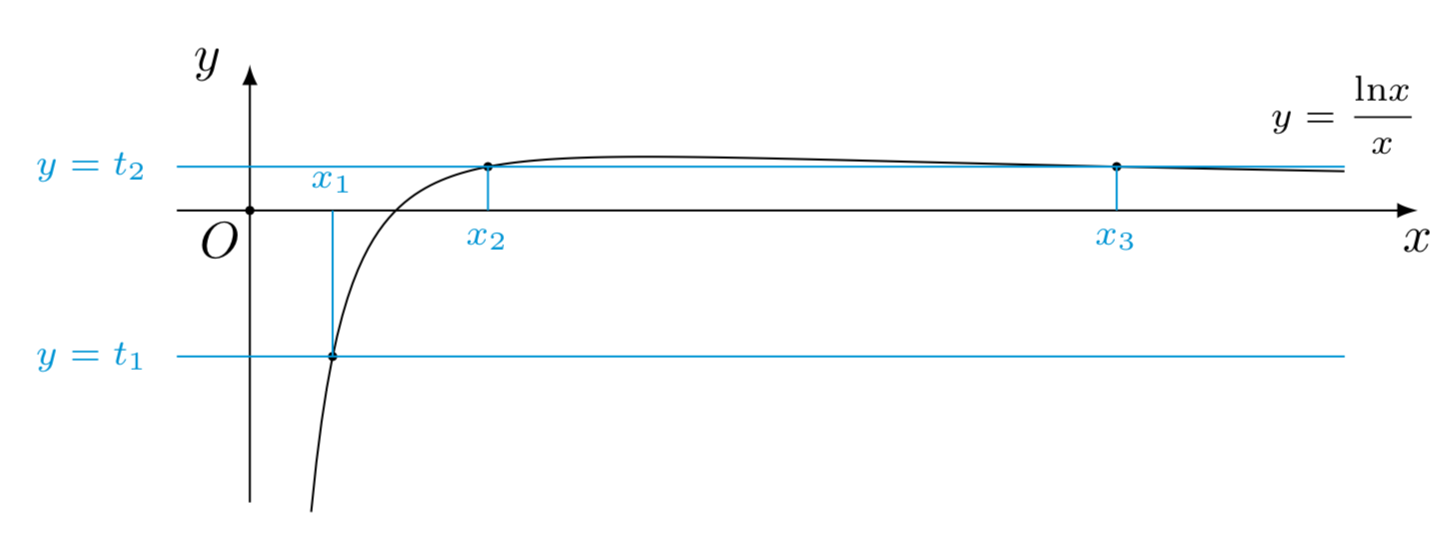
(1-t_1)2(1-t_2)2=left[1-(t_1+t_2)+t_1t_2 ight]^2=1.$$