在平面四边形 (ABCD) 中,已知 ( riangle ABC) 的面积是 ( riangle ACD) 的面积的 (3) 倍,若存在正实数 (x,y),使得 (overrightarrow{AC}=left(dfrac{1}{x}-3
ight)overrightarrow{AB}+left(1-dfrac{1}{y}
ight)overrightarrow{AD}) 成立,则(x+y)的最小值为(underline{qquadqquad}).
解析:
如图,连接(BD)交(AC)于点(G),分别过(B,D)作(AC)的垂线,
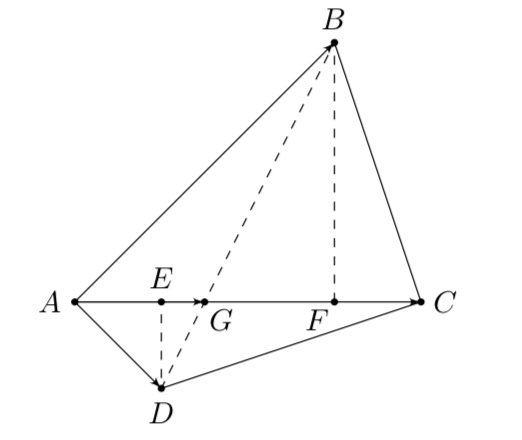
垂足分别为$F,E$.由题易知$BF:DE=3:1$,从而$BG:DG=3:1$,所以$$ overrightarrow{AG}=dfrac{1}{4}overrightarrow{AB}+dfrac{3}{4}overrightarrow{AD}.$$又因为$overrightarrow{AC}$向量与$overrightarrow{AG}$向量同向,因此$$ left(dfrac{1}{x}-3 ight):left(1-dfrac{1}{y} ight)=1:3,$$即有$$ dfrac{3}{x}+dfrac{1}{y}=10,x,y>0. $$ 从而$$10=dfrac{left(sqrt{3} ight)^2}{x}+dfrac{1}{y}geqslant dfrac{left(sqrt{3}+1 ight)^2}{x+y}.$$ 所以$x+ygeqslant dfrac{sqrt{3}+2}{5}$.等号当且仅当$$ (x,y)=left(dfrac{3+sqrt{3}}{10},dfrac{sqrt{3}+1}{10} ight)$$时取得,因此,所求表达式的最小值为$dfrac{sqrt{3}+2}{5}$.