等边 ( riangle ABC) 中, (AD,AE) 为 (angle BAC) 的三等分线, (F) 为 (AE) 中点, 连接 (BF) 交 (AD) 于点 (G), 连接 (GE), 求证: (GD=DE).
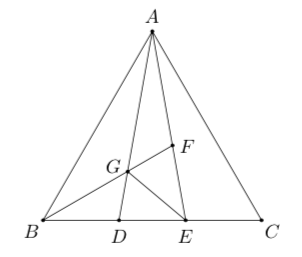
解析:
法一 考虑选定一组边长作为"基底"', 设
((AD,BD,DE)=(x,y,z).)

首先计算 (GD), 直线 (BF) 交 ( riangle ADE) 的三边 (AD,DE,EA) 于点 (G,B,F). 由梅涅劳斯定理可得
$$
dfrac{AG}{GD}cdot dfrac{DB}{BE}cdot dfrac{ EF}{FA}=1.$$
即有 (dfrac{AG}{GD}=dfrac{y+z}{y}), 给等式两边加 (1), 可得$$
GD=dfrac{y}{2y+z}cdot AD=dfrac{yz}{2y+z}.$$
接下来计算 (DE), 在 ( riangle ABE) 中, 由角平分线定理可得$$
dfrac{BD}{DE}=dfrac{AB}{AE}.$$
从而 $$
DE=dfrac{BDcdot AE}{AB}=dfrac{BDcdot AD}{BC}=dfrac{yz}{2y+z}.$$ 显然 (GD=DE), 证毕.
法二 如图, 过 (D) 作 (DHparallel AE), (AEcap DH=H).
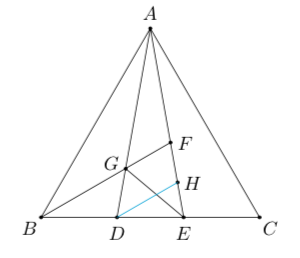
则 ( riangle AGFsim riangle ADH), ( riangle EDHsim riangle EBF). 设 (ED: DB=lambda), 则
$$
dfrac{AG}{GD}=dfrac{AF}{FH}=dfrac{EH+HF}{HF}=dfrac{ED}{DB}+1=lambda+1. quad (ast)$$ 则 $ GD=dfrac{AD}{lambda +2}$, 又在 ( riangle ADE) 中由正弦定理可得 $ DE=dfrac{ADcdot sin 20^circ}{sin 80^circ}. $
因此原题等价于求证 $$
dfrac{AD}{lambda+2}=dfrac{ADcdot sin 20^circ}{sin 80^circ}. $$ 也即求证 (lambda =dfrac{sin 80^circ}{sin 20^circ} -2). 以下计算 (lambda) 的值(:) $$
lambda =dfrac{ED}{DB}=dfrac{ED}{AD}cdot dfrac{AD}{DB} =dfrac{sin 20^circ}{sin 80^circ}cdot dfrac{sin 60^circ}{sin 20^circ}
=dfrac{sin 60^circ}{sin 80^circ} =dfrac{2sin 10^circsin 60^circ}{sin 20^circ}.$$ 从而原题即证明 (dfrac{sin 80^circ}{sin 20^circ} -2=dfrac{2sin 10^circsin 60^circ}{sin 20^circ}), 此即$$
2sin 10^circsin 60^circ =sqrt{3}sin 10^circ=cos 10^circ -2sin(30circ-10circ)=sin 80^circ-2sin 20^circ.$$证毕.
备注 在 ((ast)) 处, 计算 (dfrac{AG}{GD}) 的表达式时, 用梅氏(()梅涅劳斯())定理可一步到位.