每日一题_190919

在( riangle ABC)中,点(D)在线段(BC)上,且满足(overrightarrow{BD}=dfrac{1}{2}overrightarrow{DC}),过点(D)的直线分别交直线(AB),(AC)于不同的两点(M),(N),(overrightarrow {AM}=moverrightarrow{AB}),(overrightarrow{AN}=noverrightarrow{AC}),则((qquad))

(mathrm{A.}quad m+n=2quad) (mathrm{B.}quad2m+n=3quad) (mathrm{C.}quaddfrac{1}{m}+dfrac{1}{n}=2quad) (mathrm{D.}quaddfrac{2}{m}+dfrac{1}{n}=3)
解析:
法一 由题

[overrightarrow{AD}=dfrac{2}{3}cdotoverrightarrow{AB}+dfrac{1}{3}cdot overrightarrow{AC}=dfrac{2}{3m}cdot overrightarrow{AM}+dfrac{1}{3n}cdotoverrightarrow{AC}.$$由于$M,D,N$三点共线,故 ]

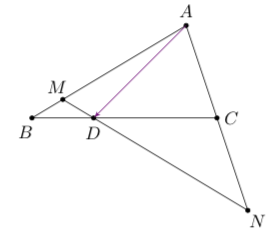
1=dfrac{2}{3m}+dfrac{1}{3n}.$$于是选项$mathrm{D}$正确.
 法二 仅需考察直线$MN$与线段$AB$相交时的情形,如图,过点$D$作$DEparallel CA$,

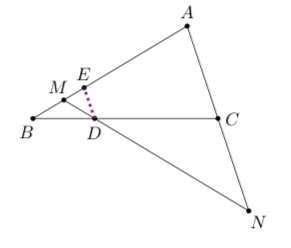
(DE)直线交(AB)于点(E),不妨设(|AE|=2),则一方面$$overrightarrow{AM}=moverrightarrow{AB},m eq dfrac{2}{3}quad (ast)$$另一方面,我们考虑用(n)将(overrightarrow{AM})与(overrightarrow{AB})联系起来.由于$$|DE|=dfrac{1}{3}cdot|AC|=dfrac{1} {3n}cdot|AN|.$$所以$$dfrac{|ME|}{|AE|}=dfrac{|DE|}{|AN|-|DE|}=dfrac{1}{3n-1},n eq dfrac{1}{3}.$$进而$$dfrac{|AM|}{|AB|}=dfrac{|AE|+|ME|}{frac{3}{2}cdot |AE|}=dfrac{n}{frac{3n}{2}-frac{1}{2}}.$$结合((ast))我们可得$$
dfrac{n}{frac{3n}{2}-frac{1}{2}}=mLongleftrightarrow dfrac{2}{m}+dfrac{1}{n}=3 .$$
所以(mathrm D)选项正确.
法三 仅考察直线(MN)与线段(AB)交于点(M)的情形,

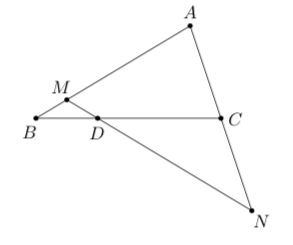
由梅涅劳斯定理我们有$$dfrac{|AM|}{|MB|}cdot dfrac{|BD|}{|DC|}cdot dfrac{|CN|}{|NA|}=1.$$也即$$dfrac{m}{1-m}cdot dfrac{1}{2}cdot dfrac{n-1}{n}=1.$$整理得$$
dfrac 2m+dfrac 1n=3.$$所以选项(mathrm D)正确.
备注 此题亦可用极限思想分析,当(M)无限接近线段(AB)上靠近(B)点的三等分点时,此时(m o dfrac{2}{3}),(n o +infty).验证仅(mathrm D)选项满足题意.