概
本文主要探讨:
- 为什么简单的FGSM不能够提高鲁棒性;
- 为什么FGSM-RS(即加了随机扰动)可以更好地提高鲁棒性;
- 一种正则化方法, 即使不加随机扰动亦可提高鲁棒性.
主要内容
对抗训练是迄今最有效的防御手段, 其思想为:
[min_{ heta} : mathbb{E}_{(x, y) sim D} [max_{|delta| le epsilon} ell(x + delta, y ; heta) ].
]
为了求解inner maximum, 一般通过PGD来近似求解. 但是这种multi-steps的方法很耗时, 所以最近也有一些方法基于FGSM进行一些改进, 其发现是FGSM在额外加一个扰动之后可以有效提高网络鲁棒性:
[delta_{FGSM-RS} := prod_{[-epsilon, epsilon]^d} [eta + alpha mathrm{sign} (
abla_x ell(x + eta, y; heta))], : eta sim mathcal{U}([-epsilon, epsilon]^d).
]
但是作者发现这种方法所带来的鲁棒性作用范围((epsilon))非常狭窄:
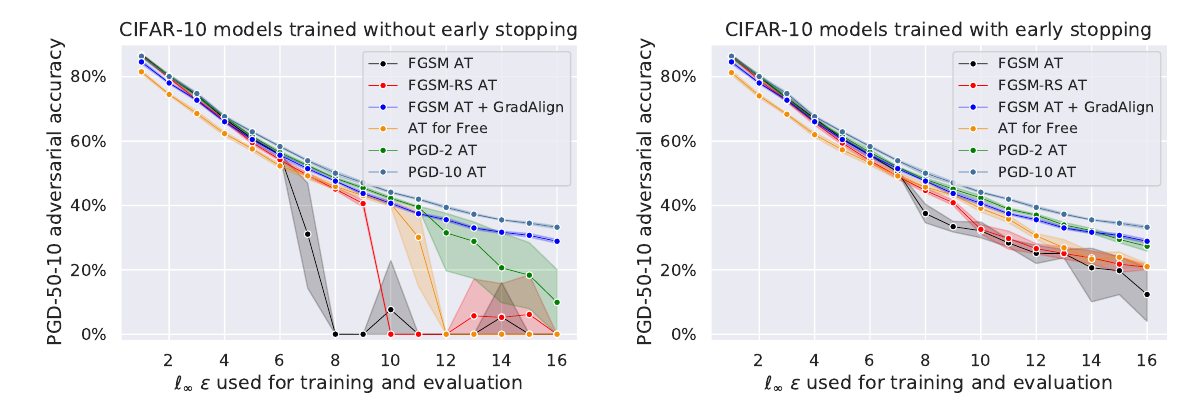
其和FGSM-AT一样, 会在某个点鲁棒性突然崩溃, 没有很好的扩展性.
Random Step的作用
为什么RS能起到一定作用, 作者认为实际上加了RS之后, (epsilon)在某种意义是'变小'了,
作者推得
[mathbb{E}_{eta} [|delta_{FGSM-RS}(eta)|_2] le sqrt{d}sqrt{-frac{1}{6epsilon}alpha^3 + frac{1}{2}alpha^2 + frac{1}{3}epsilon} in [frac{1}{sqrt{3}}sqrt{d}epsilon, sqrt{d}epsilon] le |delta_{FGSM}|_2 = sqrt{d}epsilon.
]
特别的, 作者设定小的(epsilon)试了(且不加RS)发现能与加了RS效果一致:

线性性质
接下来作者提出自己的观点, 剖析FGSM为啥有这些异常的情况出现.
作者认为一开始FGSM是对于inner maximum求解是较为准确的, 但是随着训练的深入, 不准确了, 为什么不准确, 作者认为是(ell(x; heta))关于(x)并不那么线性了.
我们知道, FGSM实际上是对于线性情况的最优解:
[delta_{FGSM} = arg max_{|delta|_{infty} le epsilon} langle
abla_x ell(x, y; heta),delta
angle,
]
当(ell)在(epsilon)球内不那么线性的时候, 这个解就不好了, 可以通过下面的条件来衡量是否线性:
[mathbb{E}_{(x, y) sim D, eta sim mathcal{U}([-epsilon, epsilon]^d)} [cos(
abla_x ell(x, y; heta),
abla_x ell(x + eta, y; heta))],
]

如上图所示, 普通的FGSM和FGSM-RS在训练过程中越发变得局部非线性, 所以求解越来越差.
gradient alignment
本文提出的解决方法就是利用上述的条件作为一个正则化项.
个人感觉这个正则化条件比以往的想法子让梯度变小更有趣一点(不局限于光滑性之上).