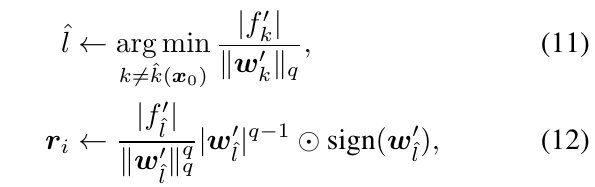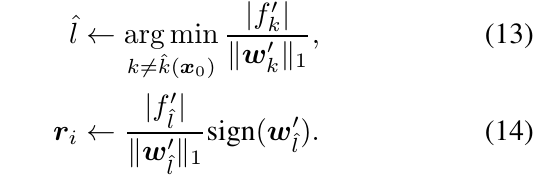Moosavidezfooli S, Fawzi A, Frossard P, et al. DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks[C]. computer vision and pattern recognition, 2016: 2574-2582.
@article{moosavidezfooli2016deepfool:,
title={DeepFool: A Simple and Accurate Method to Fool Deep Neural Networks},
author={Moosavidezfooli, Seyedmohsen and Fawzi, Alhussein and Frossard, Pascal},
pages={2574--2582},
year={2016}}
概
本文从几何角度介绍了一种简单而有效的方法.
主要内容
adversarial的目的:
[ ag{1}
Delta(x;hat{k}):= min_{r} |r|_2 : mathrm{subject} : mathrm{to} : hat{k}(x+r)
ot = hat{k}(x),
]
其中(hat{k}(x))为对(x)的标签的一个估计.
二分类模型
当模型是一个二分类模型时,
[hat{k}(x) = mathrm{sign}(f(x)),
]
其中(f:mathbb{R}^n
ightarrow mathbb{R})为分类器, 并记(mathcal{F}:= {x: f(x)=0})为分类边界.
(f)为线性
即(f(x)=w^Tx+b):
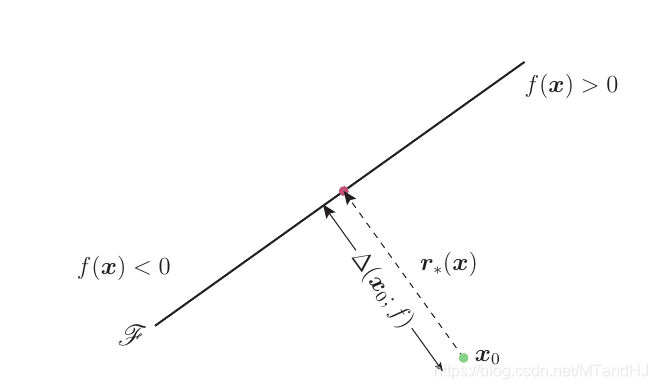
假设(x_0)在(f(x)>0)一侧, 则
[r_*(x_0)= -frac{f(x_0)}{|w|_2^2}w.
]
(f)为一般二分类
此时, 我们(f)的一阶近似为
[f(x_0+r)approx f(x_0)+
abla^T f(x_0) r,
]
此时分类边界为(mathcal{F} ={x:f(x_0)+
abla^T f(x_0) (x-x_0)=0}),此时(w=
abla f(x_0),b=f(x_0),) 故
[ ag{4}
r_*(x_0) approx -frac{f(x_0)}{|
abla f(x_0)|_2^2}
abla f(x_0).
]
所以, 每次
[r_i = -frac{f(x_i)}{|
abla f(x_i)|_2^2}
abla f(x_i), \
x_{i+1} = x_i+r_i,
]
直到(hat{k}(x_i)
ot= hat{k}(x_0))是停止, 算法如下

多分类问题
(f:mathbb{R}^n
ightarrow mathbb{R}^c), 此时
[ ag{5}
hat{k}(x) = arg max_k f_k(x).
]
(f)仿射
即(f(x) = W^Tx + b), 设(W)的第(k)行为(w_k),
[ ag{7}
P=cap_{k=1}^c {x: f_{hat{k}(x_0)}(x) ge f_k(x)},
]
为判定为(hat{k}(x_0))的区域, 则(x+r)应落在(P^{c}), 而
[Delta (x_0;f)= mathbf{dist} (x_0, P^c).
]
当(f)为仿射的时候, 实际上就是找(x_0)到各分类边界(与(x_0)有关的)最短距离,
[ ag{8}
hat{l}(x_0) = arg min _{k
ot = hat{k}(x_0)} frac{|f_k(x_0) - f_{hat{k}(x_0)}(x_0)|}{|w_k-w_{hat{k}(x_0)}|_2},
]
则
[ ag{9}
r_*(x_0)= frac{|f_{hat{l}(x_0)}(x_0) - f_{hat{k}(x_0)}(x_0)|}{|w_{hat{l}(x_0)}-w_{hat{k}(x_0)}|_2^2}(w_{hat{l}(x_0)}-w_{hat{k}(x_0)}),
]
(f)为一般多分类
[ ag{10}
ilde{P}_i=cap_{k=1}^c {x: f_{hat{k}(x_0)}(x_i) +
abla^T f_{hat{k}(x_0)}(x_i) (x-x_i)ge f_k(x_i) +
abla^Tf_k(x_i)(x-x_i)},
]
则
[r_i(x_i)=frac{|f_{hat{l}(x_i)}(x_i) - f_{hat{k}(x_0)}(x_i)|}{|
abla f_{hat{l}(x_i)}(x_i) -
abla f_{hat{k}(x_0)}(x_i)|_2^2}(
abla f_{hat{l}(x_i)}(x_i) -
abla f_{hat{k}(x_0)}(x_i)).
]

(l_p)
(p in (1, infty))的时候
考虑如下的问题
[�egin{array}{ll}
min & |r|_p^p \
mathrm{s.t.} & w^T(x+r)+b=0,
end{array}
]
利用拉格朗日乘子
[min_r : |r|_p^p + c(w^T(x+r)+b),
]
由KKT条件可知(这里的(r_k)表示第(k)个元素)
[p: |r_k|^{p-1} = c_kw_k,
]
注: 这里有一个符号的问题, 但是可以把符号放入(c_k)中进而不考虑,
故
[r_*= c odot w^{q-1},
]
其中(q=frac{p}{p-1})为共轭指数, 并(c=[c_1,ldots]^T),且(|c_i|=|c_j|,) 记(w^{q-1}=[|w_1|^{q-1},ldots]^T),又
[w^T(x+codot w^{q-1})+b=0,
]
故
[|c|=frac{|w^Tx+b|}{|w|_q^q} ,
]
故
[r_*=-frac{w^Tx+b}{|w|_q^q} w^{q-1} odot mathrm{sign}(w).
]
(p=1), 设(w)的绝对值最大的元素为(w_{m}), 则
[r_*=-frac{w^Tx+b}{w_m} mathrm{1}_m,
]
(mathrm{1}_m)为第(m)个元素为1, 其余元素均为0的向量.
(p=infty),
[r_*=-frac{|w^Tx+b|}{|w|_1} mathrm{sign} (w).
]
故:
(p in [1, infty)):
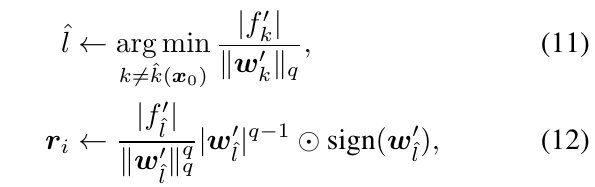
(p=infty):
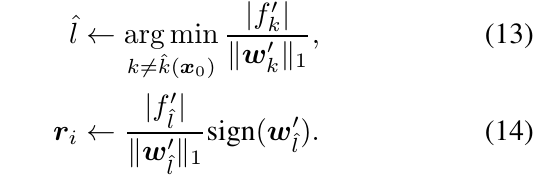
注: 因为, 仅仅到达边界并不足够, 往往希望更进一步, 所以在最后(?)(x=x+ (1+eta) r), 文中取(eta=0.02).