@article{rosasco2004are,
title={Are loss functions all the same},
author={Rosasco, Lorenzo and De Vito, Ernesto and Caponnetto, Andrea and Piana, Michele and Verri, Alessandro},
journal={Neural Computation},
volume={16},
number={5},
pages={1063--1076},
year={2004}}
概
作者给出了不同的损失函数, 在样本数量增多情况下的极限情况. 假设(p(x,y))为((x,y))的密度函数,其中(xin mathbb{R}^d)为输入样本, (yin mathbb{R})为值(回归问题) 或 类别信息(分类问题). 设(V(w,y),)为损失函数, 则期望风险为:
其中(f)为预测函数, 不妨设(f_0)最小化期望风险. 在实际中, 我们只有有限的样本(D={(x_1,y_1),ldots, (x_l,y_l)}), 在此情况下, 我们采取近似
同时
其中(mathcal{H})为hypothesis space.
(f_D)与(f_0)之间的差距如何, 是本文的核心.
主要内容
一些假设
首先(f_D)的在空间(mathcal{H})中寻找, Reproducing Kernel Hilbert Space(RKHS)一文中(没看)给出了这种空间的构造方式. 给定对称正定函数(K(x,s))(Mercer核):
同时(K(cdot, x))是连续函数.
函数(f)通过下述方式构造:
给定常数(R>0), 构造hypothesis space (mathcal{H}_{R}):
则在(|cdot|_{infty})下, (mathcal{H}_R)是连续函数(C(X))上的一个紧集,其中(Xsubset mathbb{R}^d)是紧的(这个证明要用到经典的Arela-Ascoli定理, 只需证明(mathcal{H}_R)中的元素是等度连续即可).
另外:
故
其中(C_K=sup_{x in X} sqrt{K(x,x)}).
损失函数(V)为凸函数且满足:
- (V)是Lipschitz函数, 即对于任意的(M>0), 存在常数(L_M>0)使得
对于任意的(w_1,w_2in[-M,M],yin Y)成立.
2. 存在常数(C_0), (forall yin Y)
成立.
注: 这里的凸函数, 因为一般的损失函数实际上是以(w-y)(回归), (wy)(分类)为变元, 所以要求(V(t))关于(t=w-y)或者(t=wy)为凸函数.
损失函数
回归问题:

分类问题:
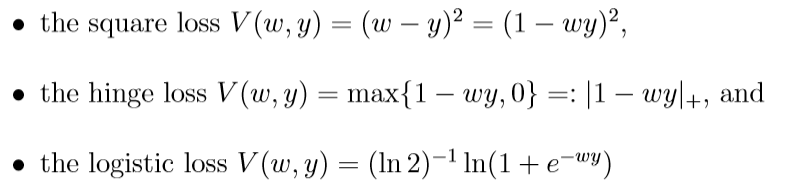
这些损失函数都是满足假设的, 所对应的(L_M, C_0), 当(Y=[a, b], delta=max {|a|, |b|})时为

(I[f_D]-I[f_R])
假设(f_R=argmin_{f in mathcal{H}_R}I[f]), 一般的误差
第一项是我们所关注的, 称为估计误差, 第二项为逼近误差.
这里引入(mathcal{H}_R)的covering number, (N(epsilon)), 文中所指的应该是wiki中的external covering number.
下面是理论结果, 引理的证明用了Hoeffding不等式, 这个不了解, 感兴趣请回看原文.
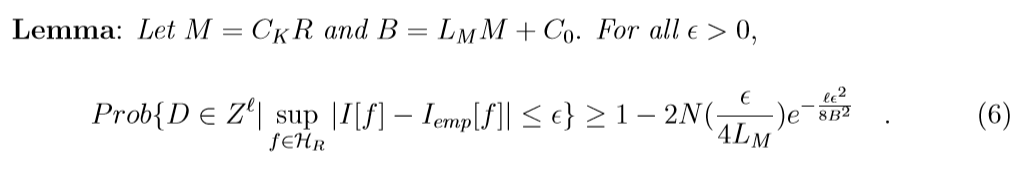

这里(epsilon(eta, ell, R))实际上(6)不等式右端第二项, 令其为(eta), 反解(epsilon)的意思.
第一个不等式实际上就是引理的推论, 第二个不等式注意到:
又(I[f_D]ge I[f_R])(这个说是根据定义, 但我没弄清楚), 故不等式成立.
损失函数的统计性质
收敛速度
考察不同损失的函数的(eta):
回归问题:
(abs / epsilon-insensitive):
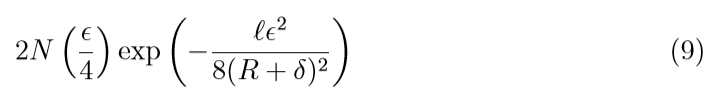
(square):
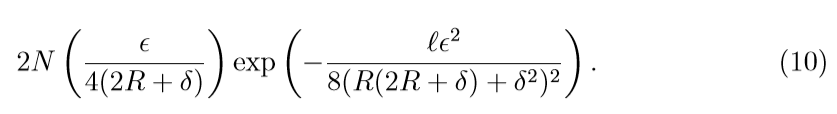
注意到, 因为square loss 的covering number 随着(R, delta)的增加会变大, 所以(eta)会变大,所以在收敛速度上, square比不上上面俩个.

分类问题:
hinge:
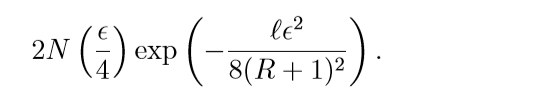
logistic:
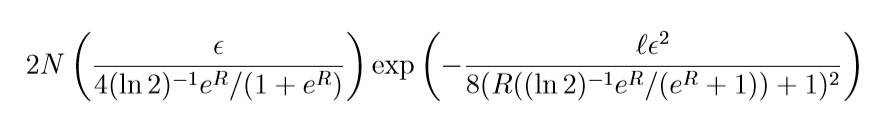
二者的收敛表现是类似的, 而square是类似的((delta=1)).
分类的界
关注分类问题中的hinge损失, 因为它会逼近概率推断.
在二元分类问题中, 其最佳函数(f_b)为:
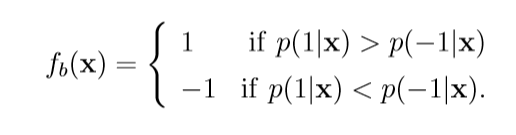
当(p(1|x)
ot= p(-1|x)).
有如下事实:

证明蛮有趣的, 这里贴一下

(p(1|x)<1/2)的证明是类似的.
另外(证明在别的论文中):
又(至少有(1-eta)的概率)
并注意到(感觉怪怪的):
故至少有(1-eta)的概率
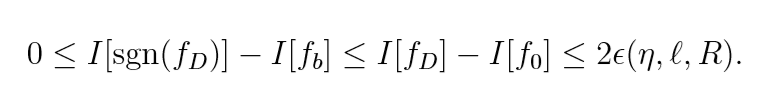
成立. 也就是说当样本个数(ell)足够大的时候, (sgn(f_D))的效用是等价于统计判别的, 这是hinge loss独有的优势.