梗概
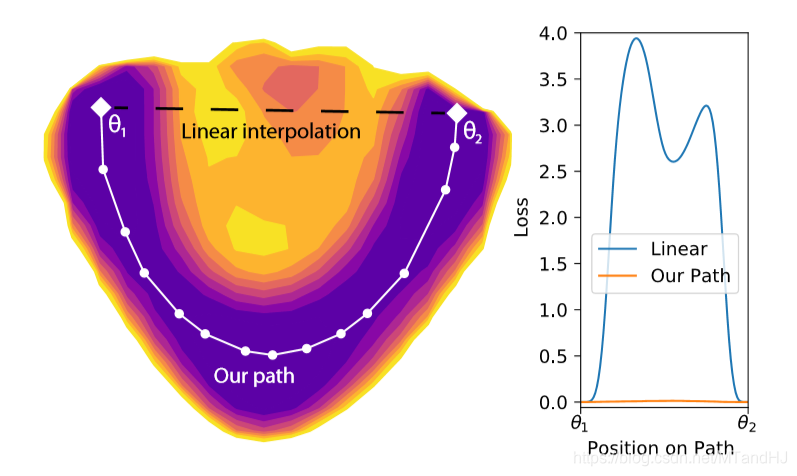
作者认为, 神经网络中,假设( heta_1, heta_2)都是使得损失达到最小的参数,那么通过一些手段,可以找到一个路径(path),沿着这条路径,其上的( heta)也会使得损失很小,几乎与最小没什么区别.
并且作者给出了如何寻找,以及一种扩展方式.
可惜的是,这些都只是猜想,有许多事实支撑,但缺乏理论论证.
主要内容
path的定义
可以说,这个定义非常之简单粗暴了.
需要一提的,作者是( heta in p( heta_1, heta_2)^*)中使得(L( heta))到达最大的点为鞍点,不过我不知道该怎么证明.
称此路径为MEP(minimum energy path).
path的逼近
上面的那个问题自然是很难求解的,所以不得不去寻找一个替代.
Mechanical Model
假设已经有一组点(p_i)(N+2)个, (p_0= heta_0, p_{N+1}= heta_2), 考虑下式:
其中,(k)是人为设定的值.
当(k)很小的时候,高能量(损失)的点之间的距离会拉大. 关于这个论点我有一点存疑,因为我觉得如果(k)真的很小很小,那么(p_i)应该会缩在一起吧,比如俩端. 当(k)过大的时候,路径会被缩短和拉紧(像弹簧),这点我是认同的,因为(p_0, p_{N+1})之间的线段会最短,这个肯定是不会太好的,因为会错过"鞍点".
Nudged Elastic Band
一个改进的版本是:
即把(E(p))分成了俩个部分, 进一步:
也就是说,认为第一部分(sum L(p_i))只提供一个垂直的力,而剩下的一部分只提供一个平行的力,就像一根弹性绳一样,一方面有一个上下拉扯的力,另一方面有一个水平伸缩的力.
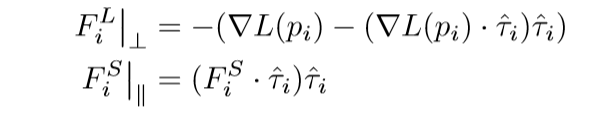
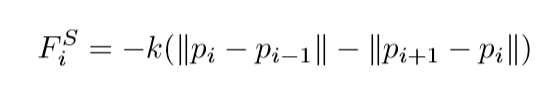
其中(hat{ au}_i)是路径的切线方向. 如何定义这个方向呢:
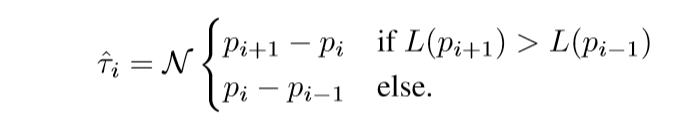
(mathcal{N}(x))将(x)归一化.
作者说,这么做,使得不会出现拉紧的情况了,值得商榷.
算法:

我奇怪的一点是,为什么更新(p_i)的时候,只受到(F_i^L|_{perp})的作用,切线方向的力呢?
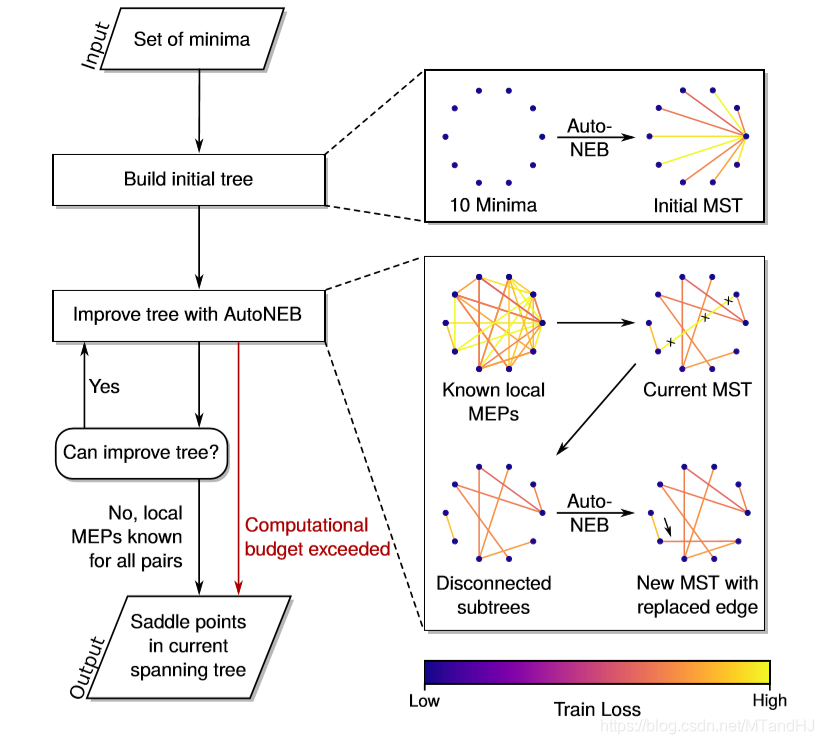
还有一个AutoNEB, 这个算法就是上面的扩展,使得我们自动增加点(p_i).

局部最优
作者说,通过上面的算法,往往会找到局部最优的MEP,但是呢,通过某些方法,我们也能使得这些局部最优显得可靠.
假设(A, B, C)三个点,代表了三个最小的参数点, 而且我们有了局部最优的路径(L_{AB}, L_{BC}), 那么:
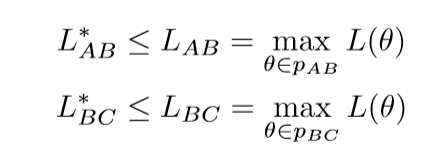
这个结论是显然的, 另外:
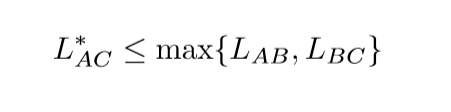
这个什么意思呢,就是(A
ightarrow B
ightarrow C)也是(A
ightarrow C)的一个路径,所以自然有上式成立.
这个有什么用呢?
假设我们有很多个最小值点(t_1, ldots, t_N), 先利用算法找到(t_1)到(t_2, ldots, t_N)的路径,这个就像一棵树(论文用树来表示,其实图更恰当吧). 可能绝大部分都是局部最优的,如何判断这些局部最优的优劣性. 首先,选出每一条路径中的最大能量点(“鞍点”)(c_2, ldots, c_N), 不妨设(t_1
ightarrow t_k)的路径拥有这些点中最大的,也就是最坏的一个路径. 我们可以试着从(t_k)往其它的寻找路径,如果能够找到一个路径(假设为(t_j)), (t_k
ightarrow t_j), 使得(t_1
ightarrow t_j
ightarrow t_k)比直接(t_1
ightarrow t_k)更优,那么我们就找到一个更好的路径,将其替换,以论下来,再对次劣的进行操作...
这样子,我们就能够有足够的理由相信,这些局部最优的路径是可靠的.

经过实验,作者发现,越深,越宽(每层的神经元个数)的网络,最优点之间的MEP越会展现出无障碍平坦的性质,即普遍的小损失.
如果确实如此,那么我们就容易构造一族解,这样网络就更灵活了不是?