Proximal Algorithms 6 Evaluating Proximal Operators

目录

• 一般方法
  • 二次函数
  • 平滑函数
  • 标量函数
  • 一般的标量函数
• 多边形
  • 对偶
  • 仿射集合
  • 半平面
  • Box
  • Simplex
• Cones
  • 二阶锥
  • 半正定锥
  • 指数锥
• Pointwise maximum and supremum
  • max
  • support function
• Norms and norm balls
  • Euclidean 范数
  • $ell_1$ and $ell_{infty}$ norms
  • Elastic net
  • 范数和
• sublevel set and epigradph
  • 下水平集
  • 上镜图
• Matrix functions
  • Elementwise functions
  • 正交不变

Proximal Algorithms

需要注意的一点是，本节所介绍的例子可以通过第二节的性质进行延展.

一般方法

一般情况下proximal需要解决下面的问题:

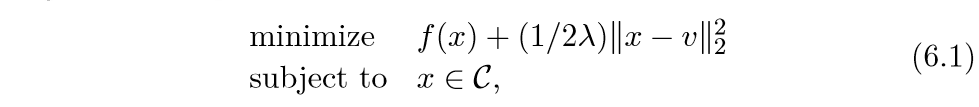
其中(x in mathbb{R}^n), (mathcal{C} = mathbf{dom} f).

我们可以使用梯度方法(或次梯度)方法来求解, 还有一些投影方法， 内点法等等.

二次函数

如果(f(x) = (1/2) x^TAx + b^Tx + c), 其中(A in mathbb{S}^n_+)，于是:

[mathbf{prox}_{lambda f}(v) = (I+lambda A)^{-1}(v-lambda b) ]

证:
设(varphi(x) = (1/2)x^TAx), 根据第二节介绍的仿射性质可得:

[mathbf{prox}_{lambda f}(v) = mathbf{prox}_{lambda varphi}(v-lambda b) ]

又(partial varphi=A), 故得证.

特别的(f(x) = b^Tx + c)则(mathbf{prox}_{lambda f}(v)=v-lambda b), (f(x)=c), (mathbf{prox}_{lambda f}(v)=v), 而当(f(x)=(1/2)|cdot|_2^2)时:

[mathbf{prox}_{lambda f}(v) = (frac{1}{1+lambda})v ]

这玩意儿有时候被称为压缩算子.

估计proximal operator的时候，需要求解一个线性方程组:

[(I + lambda A) x = v - lambda b ]

线性方程组怎么求解这里就不讨论了吧.

不过，这个应该多数用在(f(x) + g(x))这种情况吧，因为如果单纯想要最小化(f(x))，直接可以求出显示解，所以可能是(f(x) + |x|)这种类型的？

平滑函数

文章里介绍了如何用梯度方法和牛顿方法，不提了.

标量函数

(f: mathbb{R} ightarrow mathbb{R} cup {+infty}), 通过之前几节的介绍，这个情况还是蛮有意义的，因为通过proximal operator的可分性质等，有很好的扩展.
显然，此时，最优条件为:

[v in lambda partial f(x) + x ]

比如：

[f(x) = - log x \ Rightarrow mathbf{prox}_{lambda f}(v) = frac{v+sqrt{v^2 + 4lambda}}{2} ]

又比如当(f(x) = |x|):

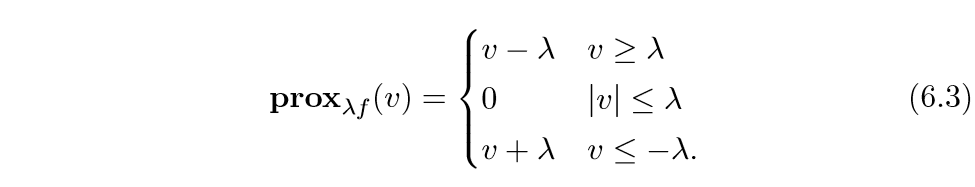
一般的标量函数

如果对于(f)，其次梯度是可获得的，那么我们可以利用localization method来有效估计(mathbf{prox}_{lambda f}), 这种方法有点类似于二分法.

我们从([l, u] in mathbf{dom} f)开始, 如果(v)在区间之外，返回最靠近(v)的点？(应该就是挑(mathbf{dom} f)中最靠经(v)的点作为边界吧) 算法会在(u-l < epsilon)的时候终止.

注：上面的第一步的意思应该是如果(v)在区间里面就取(v)，否则取中间的点.
如果(g>0),那么(varphi(z) ge varphi(x) + g(z-x)), 显然，当(z>x)不是最优的，而(z = x-lambda g)是一个下界. 为了说明这一点，假设(h_z in partial f(z)). 因为(g>0, lambda >0), 所以(z < x)，则(h_z le h)(因为凸函数的次梯度是单调的), 令:

[g_z = h_z + (1 / lambda) (z - v) in partial varphi (z) ]

于是

[h_z + (1 / lambda)(z-v) = h_z + (1/lambda) (x-lambda(h+(1/lambda)(x-v))-v) ]

等式右边是(h_z-hle0), 所以新的([l, u])就是一端小于0，一端大于0， 不过这对一开始的(l, u)有要求吧.

如果(f)是二阶连续可微的，那么，可以用guarded Newton方法来找(x^*)，不理解曲中的缘由，贴个图吧.

多边形

这一小节，考虑投影至多边形的问题，多边形可以用 一系列线性方程和不等式描述:

[mathcal{C} = {x in mathbb{R}^n| Ax=b, Cxle d} ]

其中(A in mathbb{R}^{m imes n}, C = mathbb{R}^{p imes n}).

投影问题可以表示为(计算(mathbf{prox})便会遇到此问题):

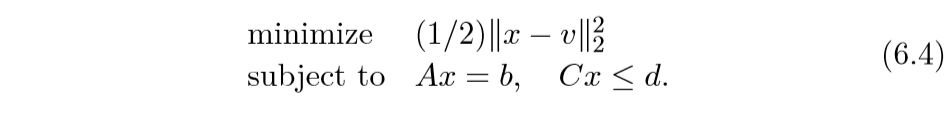
对偶

当(m, p)都远小于(n)的时候，利用对偶方法是方便的.

(6.4)的对偶问题是:

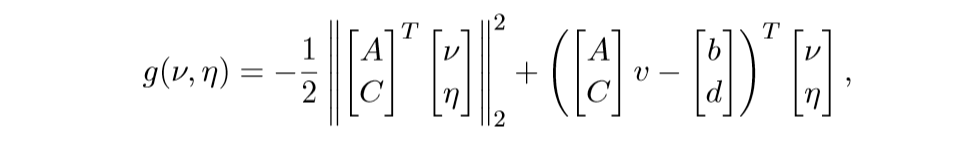
其中(v in mathbb{R}^m, eta in mathbb{R}^p)为对偶变量(上面的式子不难推出，这里不证了).

对偶问题是:

[egin{array} {lc} max & g(v, eta) \ s.t. & eta ge 0 end{array} ]

这是一个(m+p)个变量的二阶规划(QP)问题，且:

[x^* = v - A^T lambda^* - C^Tv^* ]

这个最优解的恢复是由KKT条件得来的.上面的问题，似乎可以用内点法有效解决，下次找机会再看看. 文章还提到了如何使得QP问题能够简单并行，这里便不多赘述了.

仿射集合

即

[mathcal{C} = {x in mathbb{R}^n| Ax=b} ]

则:

[Pi_{mathcal{C}} (v) = v - A^{dagger}(Av - b) ]

其中(A^{dagger})是伪逆.
如果(m<n, A)满秩，那么:

[Pi_{mathcal{C}}(v) = v-A^T(AA^T)^{-1}(Av-b) ]

这个我可以用一种比较麻烦的方法证明.
假设最优解为:(v-A^T(AA^T)^{-1}(Av-b)+u),因为

[A(v-A^T(AA^T)^{-1}(Av-b))=b ]

所以，根据线性方程组解的理论可知:

[Au=0 ]

那么问题可以转换为:

[egin{array}{lc} min & |A^T(AA^T)^{-1}(Av-b)-u|_2^2 \ s.t. & Au=0 end{array} ]

再根据线性方程组的理论可知，(u)属于(A)的核，设:

[A = UDV^T ]

其中(U in mathbb{R}^{m imes k }, D in mathbb{R}^{k imes k}, V in mathbb{R}^{n imes k}).
我们只要找出(A^T(AA^T)^{-1}(Av-b))在核空间的投影即可:

[(I-VV^T)A^T(AA^T)^{-1}(Av-b)=0 ]

即投影为0，也就是说(x=0), 这也就证明了

[Pi_{mathcal{C}}(v) = v-A^T(AA^T)^{-1}(Av-b) ]

半平面

此时(mathcal{C} = {x | a^Tx le b}), 而:

[Pi_{mathcal{C}}(v) = v- frac{(a^Tv-b)_+}{|a|_2^2} ]

其中((u)_+=max {u, 0}).

这个可以画个图来证明，注意到(frac{(a^Tv-b)_+}{|a|_2^2})和点到直线距离的联系.

Box

box为如下形式(mathcal{C} = {x | l le x le u}), 及:

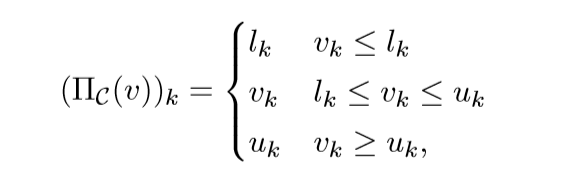
如果(mathcal{C}= mathbb{R}^n_+)则:

[Pi_{mathcal{C}}(v)=v_+ ]

这个感觉是显然的.

Simplex

Simplex 为如下形式(mathcal{C} = {z| zge 0, 1^Tz=1}), 及

[Pi_{mathcal{C}}(v) = (v - u mathbf{1})_+ ]

对于某些( u in mathbb{R}).
满足

[mathbf{1}^T(v- u mathbf{1})_+=1 ]

利用二分法可以求解.

Cones

令(mathcal{K})为锥，以及(mathcal{K}^*)为其对偶锥. 那么问题为:

[egin{array}{lc} min & |x-v|_2^2 \ s.t. & x in mathcal{K} end{array} ]

对偶锥的定义:

[mathcal{K}^* ={y| x^Ty ge 0, forall x in mathcal{K}} ]

对偶最优条件为：

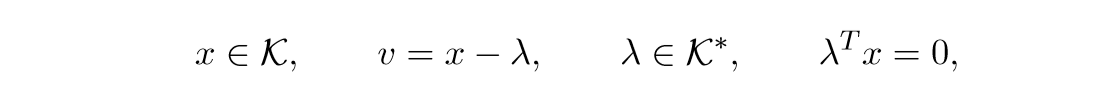
(v=x-lambda)这个条件我是存疑的，这样子原问题应该是(frac{1}{2}|x-v|_2^2)，当然，这应该无伤大雅.

二阶锥

[mathcal{C} = {(x, t) in mathbb{R}^{n+1} | |x|_2 le t} ]

上面的东西，通过考虑下面的问题:

[egin{array}{lc} min_{x,t} & |v-x|_2^2+(s-t)^2 \ s.t. & |x|_2 le t end{array} ]

可以获得， 第二种情况是不需讨论的, 那么先来看第一种情况。
在(tle |v|)的情况下，(x=tfrac{v}{|v|}), 不妨令(u=frac{v}{|v|}).则，原问题为:

[min quad (|v|-t)^2+(s-t)^2 ]

在(t=frac{|v|+s}{2})处取得极值，但是(|v|le-s)， 所以此时(tle0), 所以(t=0). (t >|v|)的时候，(x=v)，于是原问题为:

[min quad (s-t)^2 ]

那么(t=|v|)，显然没有0的时候小.

第三种情况的分析是类似的.

半正定锥

(mathcal{C} = mathbb{S}^n_+), 此时

[Pi_{mathcal{C}}(V) = sum_{i=1}^n (lambda_i)_+ u_iu_i^T ]

其中(sum_{i=1}^n lambda_i u_iu_i^T)为特征分解.

指数锥

不了解，截个图吧

Pointwise maximum and supremum

max

如果(f(x) = max_{i} x_i), 根据其上镜图，我们有等价形式:

[egin{array}{lc} min & t + (1/2lambda) |x-v|_2^2 \ s.t. & x_i le t, : i=1,ldots, n end{array} ]

其拉格朗日对偶形式为:

[L(x, t, mu) = t + (1/2lambda) |x-v|_2^2 + mu^T(x-t mathbf{1}) ]

KKT条件为:

如果(x_i^* < t^*)，则表示(通过第三个条件)(mu_i^*=0), 如果(x^*=t^*)，则表示(u_i^*=(1/lambda)(v_i-t^*)), 又(mu_i^* ge 0)， 总结为:

[mu_i^* = (1/lambda) (v_i - t^*)_+ ]

再根据第五个条件可得:

[sum_{i=1}^n (1/lambda) (v_i - t^*)_+=1 ]

这个可以用半分法求解，初始的区间为([min_i v_i -(1/n), max_i v_i]).

最后

[x^* = min {t^*, v_i}. ]

support function

(mathcal{C})是一个凸集，其support function为:

[S_{mathcal{C}} (x) = sup_{y in mathcal{C}} y^Tx. ]

support function的共轭是指示函数.

[S_{mathcal{C}}^*(z)=sup_x (z^Tx - f(x)) = I_{mathcal{C}}. ]

通过Moreau 分解我们知道:

[mathbf{prox}_{lambda S_{mathcal{C}}} (v) = v - lambda Pi_{mathcal{C}} (v / lambda) ]

一个例子是(f(x) = x_{[1]}+x_{[2]}+ldots + x_{[k]}), 表(x)的前k个最大的和，可以用以下凸集的support function来表示:

[mathcal{C} = {y | 0 preceq y preceq 1, 1^Ty=k}. ]

Norms and norm balls

(f=|cdot|)为一般的定义在(mathbb{R}^n)上的范数，则(f^*=I_{mathcal{B}}), 其中(mathcal{B})为对偶范数的单位球.

我们知道(f(x)=sup_y {y^Tx||y|_*le 1}), 此为(mathcal{B}={y | |y|_*le 1})的支撑函数，故(f^*=I_{mathcal{B}}).

对偶不是共轭的特例？

于是根据Moreau分解，有以下式子成立：

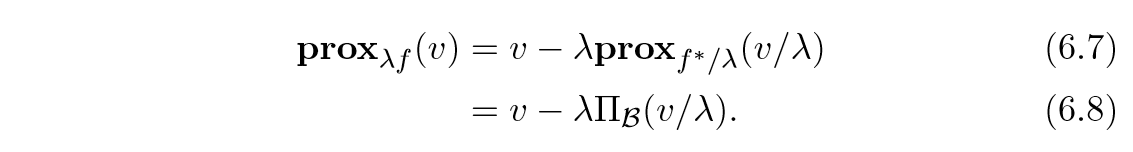
Euclidean 范数

当(f = |cdot|_2)的时候:

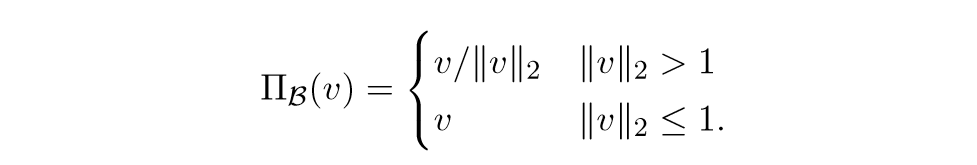
以及：

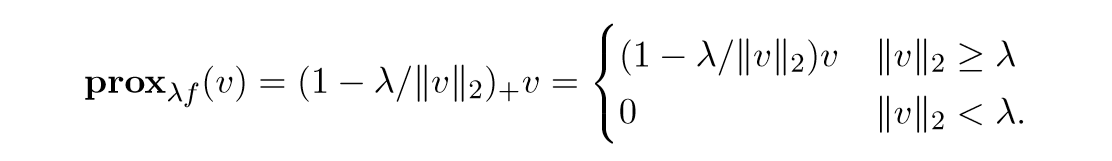
(ell_1) and (ell_{infty}) norms

(ell_{infty})的(mathcal{B})是box，所以根据之前讨论过的:

引文(ell_1)和(ell_{infty})互为对偶，所以当(f=|cdot|_1)的时候:

可以用更为紧凑的形式表示:

[mathbf{prox}_{lambda f}(v) = (v-lambda)_+ - (-v-lambda)_+. ]

欲计算(ell_{infty})的proximal operator并不容易，因为投影到(ell_1)的单位球比较麻烦.
我们需要计算一个(lambda)，满足:

[sum_{i=1}^n (|v_i| - lambda)_+=1. ]

可以用类似半分法的方法求解.

Elastic net

(f(x) = |x|_1 + (gamma/2) |x|_2^2), (gamma > 0).
此时

[mathbf{prox}_{lambda f}(v) = (frac{1}{1+lambda gamma}) mathbf{prox}_{lambda |cdot|_1}(v). ]

范数和

[f(x) = sum_{g in mathcal{G}} |x_g|_2 ]

其中(mathcal{G})是([n])的一个分割, 则:

[(mathbf{prox}_{lambda f}(v))_g = (1-frac{lambda}{|v_g|_2})_+ v_g ]

sublevel set and epigradph

下水平集

(f)的(t-)下水平集合为:

[mathcal{S} = {x in mathbb{R}^n| f(x) le t} ]

假设(v ot in mathcal{S}) , 否则(Pi_{mathcal{S}}(v)=v).
此时(Pi_{mathcal{S}}(v))可以转化为下列问题:

[egin{array}{lc} min & frac{1}{2}|x-v|_2^2 \ s.t. & f(x) le t. end{array} ]

通过KKT条件可得最优条件为:

[0 in x - v + lambda partial f(x), quad f(x)=t, quad lambda > 0 ]

第一个条件，表示(Pi_{mathcal{S}}(v) = mathbf{prox}_{lambda f}(v)), 再根据第二个条件可得:

[f(mathbf{prox}_{lambda f}(v)) = t ]

我们可以通过二分法来寻找(lambda).

上镜图

函数(f)的上镜图为:

[mathbf{epi}f={(x, t)| x in mathbf{dom} f, f(x) le t}. ]

针对(Pi_{mathbf{epi} f}(v, s)):

[egin{array}{lc} min & frac{1}{2} |x-v|_2^2 + frac{1}{2}(t-s)^2 \ s.t. & f(x) le t. end{array} ]

同样假设(f(v) > s)KKT条件为:

[f(x) = t \ 0 in x-v + lambda partial f(x) \ t-s=lambda \ lambda > 0. ]

所以

[v in x+ (f(x)-s) partial f(x). ]

论文说这个问题比较难成立，有另外一种表示方法:

不知道怎么推的.

Matrix functions

Elementwise functions

这里将矩阵(A in mathbb{R}^{m imes n})视为(mathbb{R}^{mn})的向量，就能利用之前的方法了，比如(ell_1)的方法:

[|A|_1 = sum_{i=1}^m sum_{j=1}^n |a_{ij}| ]

正交不变

函数(F: mathbb{R}^{m imes n} ightarrow mathbb{R}),正交不变是指:

[F(VXU)=F(X). ]

其中(U in mathbb{R}^{n imes n}, V in mathbb{R}^{m imes m})为正交矩阵, 这也意味着:

[F(x) = F(mathbf{diag}(sigma_s(X))). ]

其中(sigma_s:mathbb{R}^{m imes n } ightarrow mathbb{R}^{min{m, n}})是奇异值映射.
正交不变算子(F)可以表示为:(f circ sigma_s), 而

[partial F(X) = {Vmathbf{diag}(mu) U| mu in partial f(sigma_s(X)}, ]

其中(X= Vmathbf{diag}(sigma_s(X))U). 这个的推导见之前关于矩阵次梯度的介绍.

这意味着:

[mathbf{prox}_{lambda F}( A) = Vmathbf{diag}(mathbf{prox}_{lambda f}(sigma_s (A)))U. ]

这个没依照论文来，论文似乎有更加直接的证明方法，我来讲一下我的:

[egin{array}{ll} mathbf{prox}_{lambda F}(A) &= mathrm{argmin} quad lambda F(X) + frac{1}{2} |X-A|_F^2 \ end{array} ]

最优条件为:

[lambda partial F(X) +X=A. ]

假设(X= Vmathbf{diag}(sigma_s(X))U), 则:

[V(lambda mathbf{diag}(mu)+mathbf{diag}(sigma_s(X))U=A. ]

显然(A)的奇异值分解也为:

[A =Vmathbf{diag}(sigma_s(A))U \ Rightarrow lambda mathbf{diag}(mu)+mathbf{diag}(sigma_s(X))=mathbf{diag}(sigma_s(A)) ]

而

[egin{array}{ll} mathbf{prox}_{lambda f}(sigma_s(A)) &= mathrm{argmin}_{sigma_s(X)} quad lambda f(sigma_s(X)) + frac{1}{2} |sigma_s(X)-sigma_s(A)|_2^2. \ end{array} ]

其最优条件为:

[lambda u+sigma_s(X)-sigma_s(A)=0. ]

显然二者的最有条件是一样的，所以成立.
当(F: mathbb{S}^n ightarrow mathbb{R}), 且(F(UXU^T)=F(X)):

[mathbf{prox}_{lambda F}(A) = Umathbf{diag}(mathbf{prox}_{lambda f}(sigma(A)))U^T ]

其中(A=Umathbf{diag}(sigma(A))U^T).

后面还有一些关于矩阵范数，一些特殊集合的投影，以及如何求解对数障碍问题.