这一节,作者总结了一些关于proximal的一些直观解释
Moreau-Yosida regularization
内部卷积(infimal convolution):
Moreau-Yosida envelope 或者 Moreau-Yosida regularization 为:
, 于是:
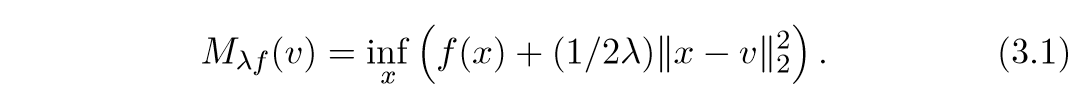
事实上,这就是,我们在上一节提到过的东西。就像在上一节一样,可以证明:
以及:
虽然上面的我不知道在(f)不可微的条件下怎么证明.
于是有与上一节同样的结果:
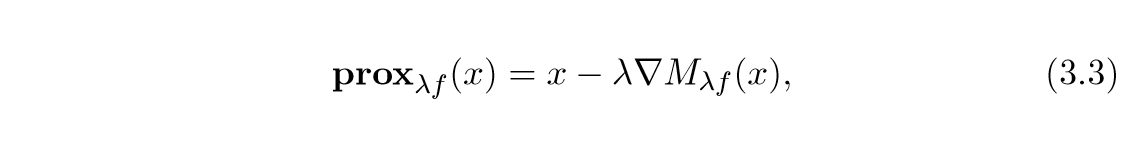
总结一下就是,近端算子,实际上就是最小化(M_{lambda f}), 等价于(
abla M_{f^*}),即:
这个,需要通过Moreau分解得到.
与次梯度的联系 (mathbf{prox}_{lambda f} = (I + lambda partial f)^{-1})
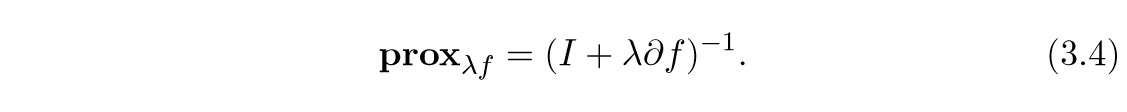
上面的式子,有一个问题是,这个映射是单值函数吗(论文里也讲,用关系来讲更合适),因为(partial f)的原因,不过,论文的意思好像是的,不过这并不影响证明:

改进的梯度路径
就像在第一节说的,和之前有关Moreau envelope表示里讲的:
实际上,(mathbf{prox}_{lambda f})可以视为最小化Moreau envelope的一个迭代路径,其步长为(lambda). 还有一些相似的解释.
假设(f)是二阶可微的,且(
abla^2 f(x) succ0)(表正定),当(lambda
ightarrow 0):
这个的证明,我觉得是用到了变分学的知识:
所以上面的是一阶距离的刻画.
我们先来看(f)的一阶泰勒近似:
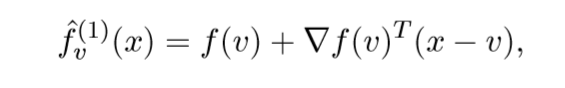
其近端算子为:
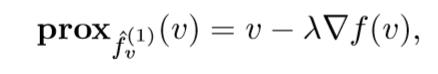
感觉,实际上是为:(mathbf{prox}_{lambda hat{f}_v^{(1)}})
相应的,还有二阶近似:
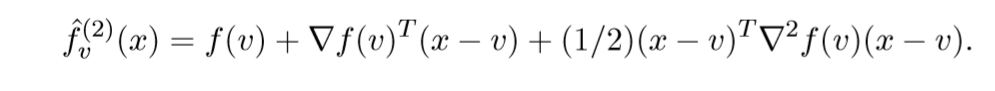
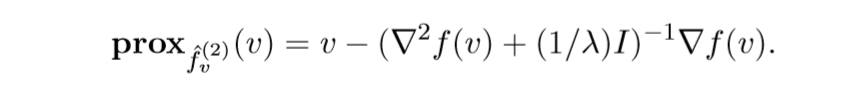
这个是Levenberg-Marquardt update的牛顿方法,虽然我不知道这玩意儿是什么.
上面的证明都是容易的,直接更具定义便能导出.
信赖域问题
proximal还可以用信赖域问题来解释:
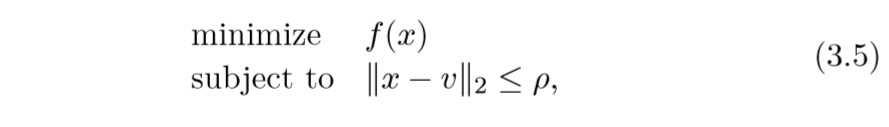
而普通的proximal问题:
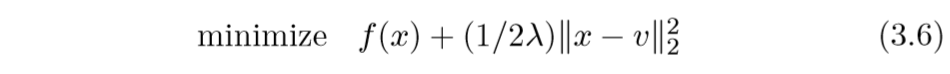
约束条件变成了惩罚项, 论文还指出,通过指定不同的参数(
ho)和(lambda),俩个问题能互相达到对方的解.