前言
上善若水任方圆。
——vfleaking 的引用
树是我们很熟悉的东西。与树有关的算法和数据结构也广为人知。
对于一般图上的某些问题,以及很多业界毒瘤仙人掌题,我们总是想将它们转化为树来做。
而圆方树就是一种将图和仙人掌变成树的方法,许多树上经典算法可以用在它身上。
所有图片都是从其他地方蒯过来的,少数语句也是由其他题解的句子缝合起来的,若侵犯了您的权益请私信联系博主!
由于本人经验不足,并不能保证每一句话都是正确的。若有错误请在评论区中说出来。
点双连通分量
一个 点双连通图 的一个定义是:图中任意两不同点之间都有至少两条点不重复的路径。
换句话说,一个点双连通图中对于任意两不同点,存在至少两条路径的交集为空(不包括出发点和到达点)。
一个近乎等价的定义是:不存在割点的图。(只在图中只有两个点,一条连接它们的边时这个定义失效。)
但是在广义圆方树中,一般都使用不存在割点这个定义。也就是说,广义圆方树中,一般都会把两个点也看成一个点双。
一个图的 点双连通分量 则是一个 极大点双连通子图。
与强连通分量等不同,一个点可能属于多个点双,但是一条边属于恰好一个点双。
仙人掌
很多人都听说过仙人掌,那仙人掌究竟是什么呢?
根据某模板题的定义:
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。
一些仙人掌和不是仙人掌的例子:
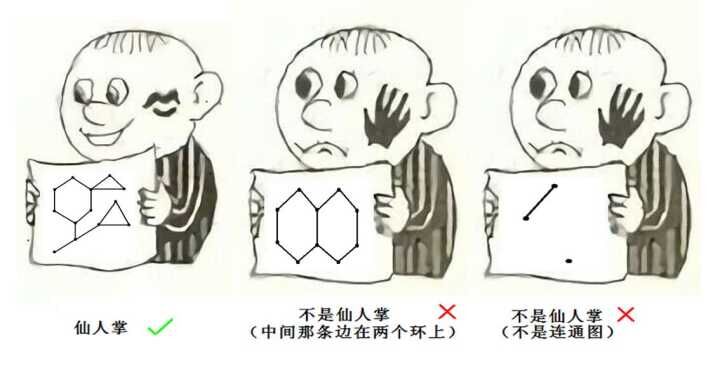
仙人掌(图)与仙人掌(植物)还是在某些方面有相似之处的。

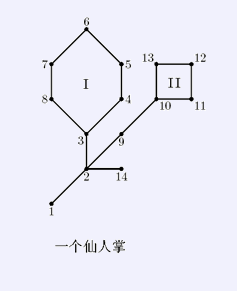
由此得知,仙人掌的一些特点:
-
仙人掌的边数 \(m\leq 2n-2\)。
-
仙人掌的一个环就是一个点双。
和一般图一样,图上两点之间的距离为这两点之间最短路径的长度。
对于一个有根的仙人掌,点 \(x\) 的子仙人掌定义为:删除从根到点 \(x\) 的所有简单路径上的所有边后,点 \(x\) 所在的连通块。
圆方树是啥
把一个无向图建成圆方树,就是原来的每个点对应一个 圆点,每一个点双对应一个 方点。
对于每一个点双连通分量,它对应的方点向这个点双连通分量中的每个点连边。
先蒯几张图过来供参考。
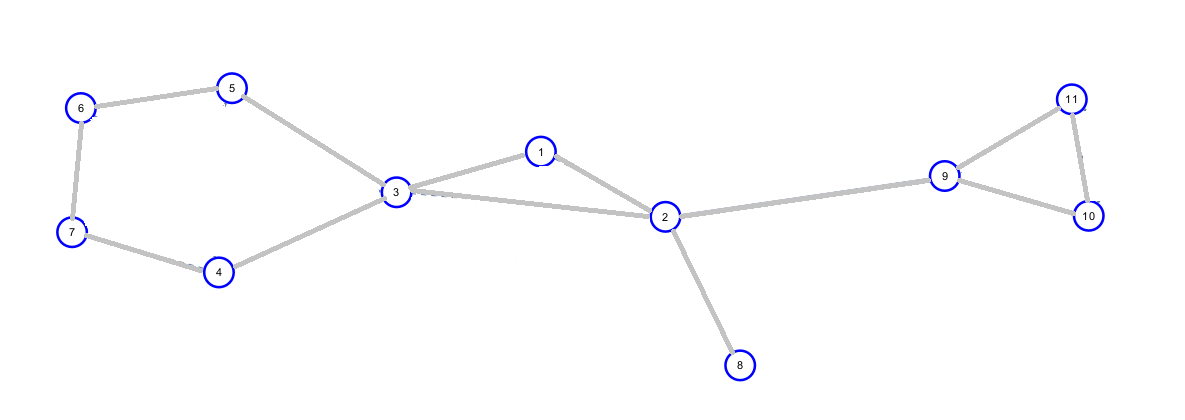

而在广义圆方树中,两个点中间的边也看成一个点双:
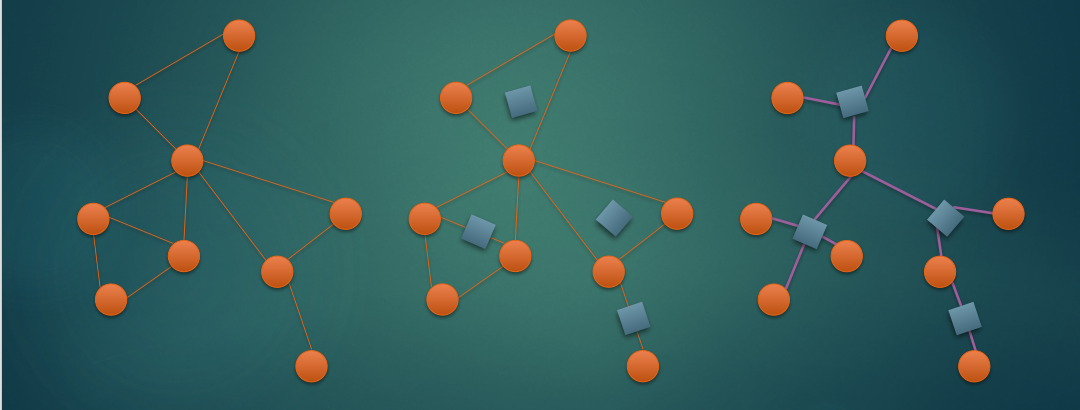
圆方树的点数为原图点数+原图点双连通分量的个数,并且小于 \(2n\),这是因为割点的数量小于 \(n\),所以请注意各种数组大小要开两倍。
方点的度数等于点双中点的总数。
方点不会直接和方点相连,因为方点只会和属于一个点双连通分量的点相连。
广义圆方树中,圆点也不会直接和圆点相连,这一点和普通的圆方树不同。
普通圆方树的构建
其实就是 Tarjan 算法的升级版。
普通圆方树的这种建法,大概是仙人掌专用,几乎没见过对一般图使用普通圆方树。
普通圆方树中,只有割边会保留下来,其他边都一定在某个点双(环)中。
所以可以 Tarjan 求割边,用 \(fa\) 数组记录 dfs 树上的父亲。
做完每个点后再遍历一遍儿子,若发现形成环,就新建一个方点,从底向上连边。
一般将环中 \(dfn\) 最小的结点作为方点的父亲结点(下文称作“父亲结点”)。
对于带边权的仙人掌,圆-方边的边权都是根据情境需要而定义,大部分题目中,圆-方边的边权定义为圆点到父亲结点的最短距离。
void build(int x, int y, int w) {
//x:父亲结点;
//y:环中最后一个结点;
//w:x 与 y 之间的边权
int cnt = w;
for (int i = y; i != x; i = fa[i]) {
sum[i] = cnt; //sum[i] 表示 dfs 树中,父亲结点到 i 点的路径长度,相当于一个环上前缀和
cnt += fw[i];
}
stot[x] = sum[x] = cnt; //父亲结点的 stot,sum 值可能在之后由于其他环而更新,如果父亲结点的父亲也是方点,则这两个值最终由父亲结点的父亲方点所决定
tr.add(x, ++cnd, 0); tr.add(cnd, x, 0);
for (int i = y; i != x; i = fa[i]) {
stot[i] = cnt; //stot[i] 表示 i 所在环的总长,每个方点所有儿子圆点的 stot 值相等
tr.add(i, cnd, min(sum[i], stot[i] - sum[i])); //选取该圆点到父亲结点的最短距离作为边权
tr.add(cnd, i, min(sum[i], stot[i] - sum[i]));
}
}
void tarjan(int u, int fm) {
dfn[u] = low[u] = ++num;
for (int i = cac.head[u]; i; i = cac.pre[i]) {
int v = cac.to[i];
if (!dfn[v]) {
fa[v] = u; fw[v] = cac.val[i]; //记录 dfs 树上的父亲以及父亲连向自己的边权
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) tr.add(u, v, cac.val[i]), tr.add(v, u, cac.val[i]); //割边保留下来
}
else if (i != (fm ^ 1)) low[u] = min(low[u], dfn[v]);
}
for (int i = cac.head[u]; i; i = cac.pre[i])
if (dfn[cac.to[i]] > dfn[u] && fa[cac.to[i]] != u) //判断是否成环,如果有重边则需要判断该边是否为 dfs 树边
build(u, cac.to[i], cac.val[i]);
}
广义圆方树的构建
其实比普通圆方树还简单。
大体思路就是,如果发现结点 \(u\) 的儿子 \(v\) 的子树中存在连向 \(u\) 的反祖边,那么 \(u\) 与 \(v\) 的子树所有点组成了一个点双连通分量。
那么新建一个方点,在圆方树中将方点与这个点双连通分量的所有点连边。
这种构建方法适用于一般的无向图。
void tarjan(int u) {
dfn[u] = low[u] = ++num;
sta[++tp] = u;
for (int i = cac.head[u]; i; i = cac.pre[i]) {
int v = cac.to[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] == dfn[u]) { //这个时候 v 的子树中存在连向 u 的反祖边
++cnd; //新建方点
for (int x = 0; x != v; tp--) { //把栈中 v 的子树的所有点弹掉并与方点连边
x = sta[tp];
tr.add(x, cnd);
tr.add(cnd, x);
}
tr.add(u, cnd); //u 也要与方点连边,但不从栈中弹掉
tr.add(cnd, u);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
int main() {
......
cnd = n;
tarjan(1);
......
}
例题
洛谷P4320 道路相遇
题目大意
给出一个无向连通图,无重边无自环,若干组询问,查询两个结点之间所有简单路径中必须经过的结点数。
思路
其实问的就是两个结点之间的简单路径中割点的数量,当然也得算上起点与终点。
这里要用到圆方树的一个性质:原图的割点就是圆方树中度数大于 \(1\) 的圆点。
因为圆方树中度数大于 \(1\) 的圆点都至少存在于两个点双连通分量中,把这个圆点去掉,两个点双连通分量不再连通,故以上结论成立。
那么问题又转化成了:求圆方树上两点之间圆点的数量。
我方法是给圆点赋 \(1\) 的权值,给方点赋 \(0\) 的权值,接着统计路径点权和。
另一种方法是:\(圆点的数量=两点之间的距离 \div 2+1\),因为一条链上圆点和方点是相间的。
于是就可以愉快地求 LCA(倍增/树剖)统计答案了(听说卡常?)。
UVA1464 Traffic Real Time Query System
题目大意
给出一个无向图(未必连通),若干组询问,查询两条边之间所有简单路径中必须经过的结点数。
思路
与上题区别不大,但是询问由点变成了边。
我的方法是直接把每条边也建点,接着就跑上题代码。后来发现不用另外建点,只要把起点终点设为边所在点双对应的方点就行。
洛谷P4606 [SDOI2018]战略游戏
题目大意
给出一个无向连通图,若干组询问,给一个点集,求有多少个不属于该点集的点删去后使得点集中存在两个点不连通。
思路
这题与道路相遇的区别就是两个结点变成了 \(\left| S\right|\) 个结点。
也就是说我们要求这 \(\left| S\right|\) 个点的极小连通子图上的圆点数量。
(这种题好像可以直接虚树解决,然而做这题时我还不会虚树。)
这让我们不得不想起一个经典问题:求所有关键点形成的极小连通子树的边权和。
有一个结论:dfs 序求出后,假设关键点按照 dfs 序排序后是 \(\left\{a_{1},a_{2},\ldots ,a_{k}\right\}\)。
那么所有关键点形成的极小联通子树的边权和的两倍等于 \(dist\left( a_{1},a_{2}\right)+dist\left( a_{2},a_{3}\right)+\ldots +dist\left( a_{k-1},a_{k}\right)+dist\left( a_{k},a_{1}\right)\)。
于是对于本题,可以把圆点的权值转化成它和它的父亲方点的边权,用上述方法统计边权,最后特判所有关键点的最近公共祖先,因为没有统计到它。
洛谷P4630 [APIO2018] Duathlon 铁人两项
思路
注意图不一定连通。
先考虑树怎么做。
枚举中转点 \(c\),对于 \(c\) 的每一个儿子 \(x\),其子树内的所有点作为 \(s\) 都能和其他子树中的节点组成合法的 \(\left(s,f\right)\)。
这样很容易想到一个做法:把 \(c\) 当作根,则 \(c\) 作为中转点的答案是 \(\sum _{fa\left[ x\right]=c }size\left[ x\right]\times \left(size\left[ c\right]-1-size\left[ x\right] \right)\)。
这个过程可以用换根 dp(算不上换根 dp,应该说就是新开个数组记一下父亲连通块的点数)解决。
对于任意图,肯定是要先建出圆方树。
那么除了圆点,还要考虑方点的贡献。其实就是一个子树上的点,到达另一个子树上的点,途径该点双中其他任意一个点。
则 \(c\) 这个方点作为中转点的答案是 \(\sum _{fa\left[ x\right]=c }size\left[ x\right]\times \left(size\left[ c\right]-size\left[ x\right] \right)\times \left(deg\left[ c\right]-2 \right)\)。
CF487E Tourists
题目大意
给出一个无向连通图,点有点权。若干操作,包括单点改点权、求两点之间所有简单路径的最小点权。
思路
建出圆方树,方点点权设为点双中的最小点权,这种问题似乎直接树剖套个线段树就行了。
但是考虑修改操作,一个圆点改了点权,有关方点的点权也要改变。
对每个方点维护一个 multiset,里面存所有与之相邻的圆点权值,每次修改就删掉原来的权值,插入新的权值。
然而这样会被卡 TLE。比如菊花图,有一个圆点与 \(n-1\) 个方点相连,每次修改就都要修改 \(n-1\) 个方点。
于是,对于一个方点,multiset 里面存它所有子节点的权值。这样修改一个圆点时,就只需要动它父亲的 multiset。
查询时,如果这两个点的 LCA 是方点,就还要算上 LCA 的父亲的贡献。
洛谷P5236 【模板】静态仙人掌/BZOJ2125 最短路
仙人掌圆方树入门题。
思路
参考“普通圆方树的构建”部分,我们已经为仙人掌建了一棵圆方树。由圆-方边的边权的定义可知,圆方树中某个圆点到其某个祖先圆点的距离等于仙人掌中该两点的距离。
所以转化成圆方树后,要查询两点之间的最短路,可以使用求 LCA 的方法(倍增/树剖)统计路径长度。
(仙人掌剖分实现起来较复杂,建议直接倍增。当然下面有一题你不得不仙人掌剖分。)
不过求解时在 LCA 处需要特判一下:
-
若 LCA 是圆点,与普通树上问题无异。
-
若 LCA 是方点,则需要找出 LCA 到两点路径上的两个儿子,并比较出两个儿子在环上的实际距离。
环上两点的距离可以利用 \(sum\) 和 \(stot\) 两个数组计算得出。
BZOJ4316 小C的独立集
这题也有直接在图上 dp 的做法,但是建出圆方树之后的状态要少一维。
树上问题非常简单:设 \(f\left[ i\right] \left[ j\right]\) 表示 \(i\) 号点取的状态为 \(j\),\(i\) 的子树的最大独立集。
(其中取的状态 \(j\in \left\{ 0,1\right\}\),\(0\) 表示不取,\(1\) 表示取不取皆可。)
同样搬到圆方树上,要分别考虑圆点和方点的贡献。
状态及其在圆点上的含义以及在圆点上的转移与树上问题的做法完全一样。
而对于一个方点,\(f\left[ i\right] \left[ j\right]\) 表示 \(i\) 号点所代表环与父亲相邻的圆点取的状态为 \(j\),\(i\) 的子树的最大独立集。
转移的时候把方点的所有儿子圆点排成一条链,做一个子动态规划。转移较为显然,此处不再赘述。
洛谷P4244 [SHOI2008]仙人掌图 II
这题完全不需要建出圆方树,但是可以强行套上圆方树。
可以建广义圆方树,也可以使用“最短路”的方法建普通圆方树,如果边有边权,则后者更容易维护。
设 \(f\left[ i\right]\) 表示 \(i\) 的子树中,与 \(i\) 距离最大的点到 \(i\) 的距离,\(ans\) 表示最终的答案。
对于一个圆点,很显然:
//v 是圆方树上 u 的一个儿子
ans = max(ans, f[u] + f[v] + 1);
f[u] = max(f[u], f[v] + 1);
而对于一个方点,要用所有从环上一个圆点经过这个环再从环上另一个圆点出去的最长路径更新 \(ans\)。
即 \(ans=\max \left\{ f\left[ i\right]+f\left[ j\right]+dist\left( i,j\right) \right\}\)。
看到这里,很容易想到把方点的儿子圆点(可以包括父亲)按顺序放进一个 \(a\) 数组,再复制成倍。
对于每个圆点 \(i\),都需要找到一个尽可能大的 \(f\left[ j\right]+dist\left( i,j\right)\),并且 \(dist\left( i,j\right)\) 不能超过环长的一半。
很明显是个单调队列优化 dp。
而 \(f\) 数组,只需要枚举儿子圆点 \(v\),用 \(f\left[ v\right] + dist\left( v,fa\right)\) 更新即可。
这样一来,其实圆方树显得挺多余,环上的转移可以直接转移到方点父亲的 \(f\) 数组。
UOJ87 mx的仙人掌
看到仙人掌,想到建立圆方树。
看到 \(tot\leq 某个数\) 想到可以建虚树。
求这几个点中,两个点之间最短路的最大值就可以转化成在虚圆方树上求直径。
显然可以用上题的方法。
但是如果虚树完全照搬板子,会出现方点的圆儿子并不在那个环上,甚至方点直接连方点的情况。
所以一个方点某个圆儿子子树中有关键点时,那个圆儿子也要加入虚树中。
具体地,虚树加入新点时,如果求得 LCA 是方点,那么得让方点的两个圆儿子也加进去。
虽然是个三合一,但是代码中各种改动、细节、坑点较多,加上数据极强,导致笔者调了很久。
UOJ158 【清华集训2015】静态仙人掌
这种题看上去像树剖,但是仙人掌的链剖分并不是很好做:对于某个环上的点来说,同样是经过这个环的路径,有的会经过它,有的又不会经过它。
于是建一棵广义圆方树(普通圆方树也可以,但情况稍复杂),把所有点分成三类:
-
每个圆点的种类由 dfs 过程第一个访问到它的环所决定。根属于第 \(0\) 类。
-
方点和方点的重儿子为第 \(0\) 类。
-
在环上,方点的重儿子到方点的父亲的最短路径中出现的点为第 \(1\) 类。
-
在环上,方点的重儿子到方点的父亲的最长路径中出现的点为第 \(2\) 类。
接着要安排点的顺序。此时对于一个环,要把所有环上的点都放进来,再去考虑子树。
具体地,对于一个方点,先依次把它自己和它的所有儿子加入 dfs 序中,然后再按照重边先行的顺序访问儿子的子树(不包括那些儿子了)。
对于一个圆点,就不用再更新 dfs 序,直接按照重边先行的顺序访问儿子的子树。
为了后来更好操作,可以同时记 \(posl\) 和 \(posr\) 数组:对于一个方点,它表示环上的儿子结点 dfs 序的左右端点;对于一个圆点,它表示其子仙人掌除了它自己之外的结点 dfs 序的左右端点。按照以上构建方法,这些点的 dfs 序应该是连续的。
所以在操作 \(3\) 中,要将 \(x\) 本身和其子仙人掌其他点分开考虑。
这样,一条最短路径的重链只会经过第 \(0\)、\(1\) 类点,一条最长路径的重链只会经过第 \(0\)、\(2\) 类点,并且这些点的 dfs 序中间没有未经过的同类点。
于是,可以用三棵线段树分别维护这三类点的信息。
最后要考虑的一个问题是,跳重链时,两个重链之间可能有一系列点。
如果链顶是方点,那直接往上跳即可。
但链顶是圆点,那它到所在环的顶部有一定的距离,需要几个分类讨论。
UOJ23 【UR #1】跳蚤国王下江南
如果是树上问题,那只要一个 dfs 就完事,但是这个方法直接放在仙人掌上可能达到指数级别的复杂度,也不好改良。
建出圆方树,设 \(f\left( i,j\right)\) 表示从 \(i\) 出发往下走 \(j\) 步的路径条数。
对于某一个点 \(i\),可以用类似于 vector 的东西存下每个 \(f\left( i,j\right)\) 的值。
考虑 \(u\) 如何转移:
把每个儿子的向量求出之后,对于每个儿子 \(v\),\(f\left( u\right)\) 加上 \(f\left( v\right)\) 右移 \(dist\left( u,v\right)\) 位后的向量。
如果 \(u\) 是方点,同时加上 \(f\left( v\right)\) 右移两种距离后的向量。
这种方法的时间复杂度显然是 \(O\left( n^{2}\right)\) 的。
考虑进行点分治。
函数 \(dfz\left(x\right)\) 返回 \(x\) 所在连通块中,点 \(x\) 的向量,\(x\) 称为连通块的根。
先找到重心 \(u\),那么 \(x\) 开始的路径分为两类:经过 \(u\) 的路径与不经过 \(u\) 的路径。
对于后者,直接递归 \(u\) 的父亲连通块即可。
对于前者,再把每条路径分为若干段:从 \(x\) 到 \(u\) 的段以及从 \(u\) 开始往下的段。
对于从 \(u\) 开始往下的段,递归 \(u\) 的每个儿子的子树,再按照上文的 dp 做法转移到 \(u\)。
对于从 \(x\) 到 \(u\) 的段,就让一个点 \(v\) 从 \(u\) 开始不断跳父亲,对于每一条父亲向儿子的边,当成一个很小的连通块,按照父亲点的种类分类讨论建立一个向量。
于是得到了一组向量,它们的总大小不超过父亲连通块大小的 \(2\) 倍。
用分治 NTT 把这些向量的卷积求出来,得到连通块的根到重心这一条链上的向量,再乘上 \(u\) 子树的向量,最后加上不经过 \(u\) 的路径的答案,即为函数的返回值。
点分治再套上分治 NTT,时间复杂度 \(O\left( n\log ^{3}n\right)\),但由于常数小,所以有可能卡过去。
这个方法可以优化成 \(O\left( n\log ^{2}n\right)\)。
令 \(top\left[ u\right]\) 表示当 \(u\) 为重心时连通块的根。
则求出连通块的根到重心这一条链上的向量后,把它记为 \(up\left[ u\right]\),这样的空间复杂度是 \(O\left( n\log n\right)\)。
求解 \(up\left[ u\right]\) 时,如果 \(top\left[ v\right]=v\),就按照上文的方法跳父亲,否则让它不停跳 \(top\),取下 \(up\left[ v\right]\)。
这样分的段数大约为 \(\log 链长\),并且后一段大约是前一段的两倍(参考点分治的过程)。
这样做只得到 \(\log 链长\) 个向量,按顺序暴力 NTT 卷积起来即可。