四边形不等式
使用范围:区间序列(DP)求最小值(一定是最小值)
对于动态规划转移方程
dp[i][j]=min(dp[i][k],dp[k+1][j])+w(i,j);
其中(w(i,j))只受(i,j)取值影响
如果满足下面两个条件
(1.)区间单调性:如果对于(forall i leq i'< j' leq j,w(i',j') leq w(i,j))(即小区间取值(leq)大区间取值)
(2.)四边形不等式:(forall i leq i'< j' leq j,w(i,j)+w(i',j')leq w(i',j)+w(i,j'))
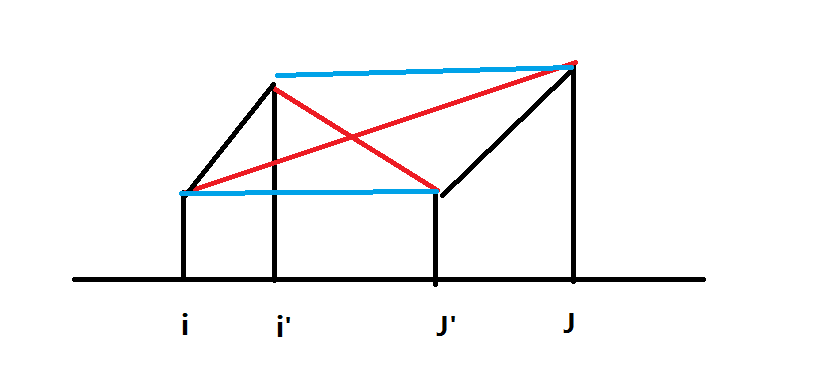
即中的红线总长(geq) 蓝线总长
如果(w(i,j))同时满足区间单调性和四边形不等式
那么(f(i,j))满足四边形不等式
令(S(i,j))为(F(i,j))在取到最优解时的决策点(k)
那么决策本身具有单调性,即满足(S(i,j)leq S(i,j+1)leq S(i+1,j+1))
用(j)代替(j+1)得到
(S(i,j-1)leq S(i,j)leq S(i,j+1))
转移方程变为
(F(i,j)=min(F(i,k)+F(k+1,j))+w(i,j); (S(i,j-1)leq kleq S(i+1,j)))
可以证明,他将时间复杂度降到了(O(n^2))

什么时候使用四边形不等式?
只需要牢记公式
(S(i,j-1)leq S(i,j)leq S(i,j+1))
考试时可以打一张决策表看是否满足上面式子,满足可以使用四边形不等式
(1.)序列(DP)有时可以使用四边形不等式优化,但仅仅是常数优化
(2.)需要注意四边形不等式仅针对求最小值的情况
(3.)注意(S)数组(下标取值范围)需要初始化,(S[i][i]=i)
例题
P1880石子合并
这道题的四边形不等式非常裸,但要注意求最大值不能用四边形不等式,注意到最大值可以使用决策单调性优化

求最大值时(f[i][j])一定是从(f[i][j-1])或(f[i+1][j])转移过来的,所以可以将第三维优化掉
(Code)
#include<iostream>
#include<cstdio>
#define maxn 2005
#define INF 0x3f3f3f3f
#define re register
using namespace std;
int a[maxn],sum[maxn];
int f1[maxn][maxn],f2[maxn][maxn];
int s[maxn][maxn];
int n,tmp,pos,tmp2;
int ans1=0x3f3f3f3f,ans2;
int main()
{
scanf("%d",&n);
for(re int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
a[i+n]=a[i];
}
for(re int i=1;i<=2*n;++i)
{
sum[i]=sum[i-1]+a[i];
s[i][i]=i;//决策区间初始化
//这里的f[i][i]都是0不用初始化因为求max就是初始化为0
//求min使用决策单调性不需要初始化了
}
for(re int i=2*n-1;i>=1;--i)
for(re int j=i+1;j<=2*n;++j)
{
f2[i][j]=max(f2[i][j-1],f2[i+1][j])+sum[j]-sum[i-1];
/*注意这句,
求最大值不能用四边形不等式,
因为最大值不满足单调性,
但最大值有一个性质,
即总是在两个端点的最大者中取到。
*/
tmp=INF,pos=0;
for(re int k=s[i][j-1];k<=s[i+1][j];++k)
{
tmp2=f1[i][k]+f1[k+1][j]+(sum[j]-sum[i-1]);
if(tmp2<tmp) tmp=tmp2,pos=k;
f1[i][j]=tmp;
s[i][j]=pos;
}
}
for(re int i=1;i<=n;++i)
{
ans1=min(ans1,f1[i][i+n-1]);
ans2=max(ans2,f2[i][i+n-1]);
}
printf("%d
%d",ans1,ans2);
return 0;
}