那么答案一定是这个函数和(X)轴的交点,因为{(Xi)}不同,所以这个函数的斜率和截距也就不同,因为(Sigma value_i*x_i)和(Sigma cost_i*x_i)非负的原则,那么我们的图像是这样的。
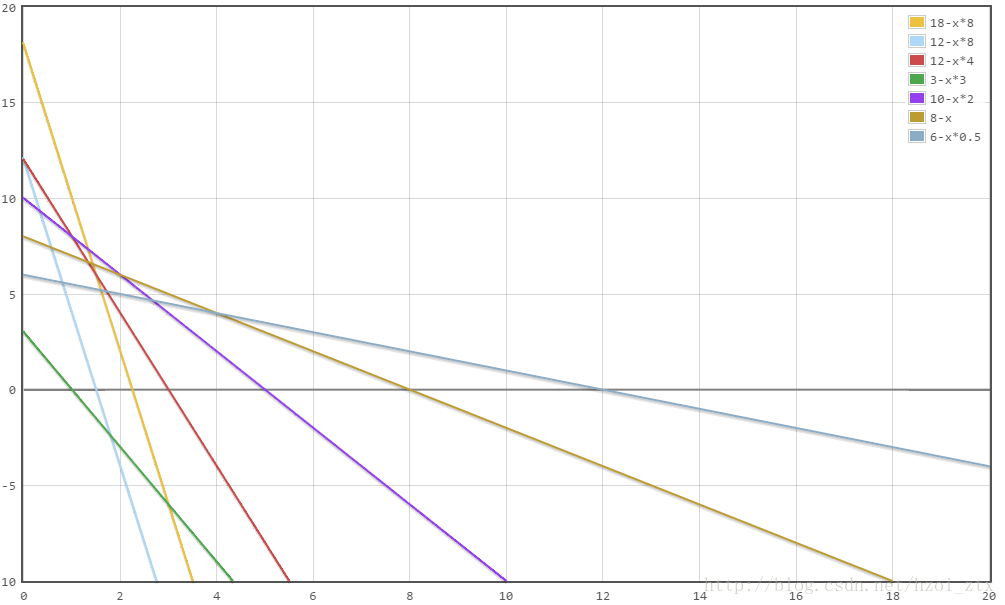
让答案的(r)最大,我们就应该让与(X)轴交点最大
将以上式子化简为(Sigma x_i(value_i-cost_i*r))。
我们二分一条平行于(X)轴的直线(x=a),如果(f(a)>0) 说明还可以将直线右移,如果(f(a)<0)那么说明与(X)轴交点应该在左边,如果等于就说明这里就是(r)的最大值。
(f(a))怎么求呢?我们可以用贪心的思想,设(v_i=value_i-cost_i*r),然后取(v_i)前(m)大即可,这样确保(f(a))的值尽量大,(x=a)尽量往右移,最终知道(Sigma v_i=0),这样就能确保答案的(r)最大了。
(Code)
还没写就先这样吧