离散型随机变量
- 如果一个随机变量X全部可能取值为有限个或可列多个。
- 离散型概率分布:P(X=xk)=pk
(0-1)分布
- 随机变量X的所有可能取值为0或1
- P(X=k)=pk(1-p)1-k,k=0,1
二项分布
- 用于描述可重复进行独立试验的随机现象。在n次独立重复的伯努利试验中,设每次试验中事件A发生的概率为p。
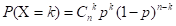
超几何分布
- 有N件产品,有M件次品,随机取n件进行抽查,其中有k件次品

泊松分布
- 若随机变量X的所有可能取值为一切非负整数。以固定的平均瞬时速率λ(或称密度)随机且独立地出现时,那么这个事件在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分布P(λ)。
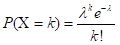 (X服从参数为λ的泊松分布)
(X服从参数为λ的泊松分布)
几何分布
- 在重复独立试验中,考察事件A发送与否,且P(A)=p。以X表示事件A首次发生时的试验次数。
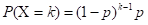
巴斯卡分布
- 进行重复独立试验,事件发生一次的概率为p,则考察事件发生r次的概率
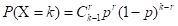
连续型随机变量及其分布
设随机变量X的分布函数为F(X),如果存在非负函数f(x),使得对任意实数x,有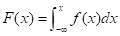 ,则称X是连续型随机变量,称f(x)为X的概率密度函数。
,则称X是连续型随机变量,称f(x)为X的概率密度函数。
概率密度f(x)性质:
- f(x)>=0
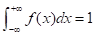
- 对任意实数x1,x2(x1<x2)有:
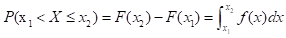
- 若f(x)在点x处连续,则有F'(x)=f(x)
均匀分布
若随机变量X的概率密度函数为: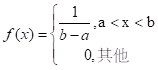
X的分布函数为: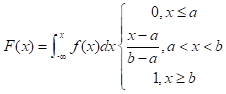
X落在(a,b)中任一子区间(c,c+l)内(其中a<c<c+l<b)的概率仅与子区间的长度l成正比,而与子区间的位置无关,这说明X落在两个长度相等的子区间内的概率是相等的。
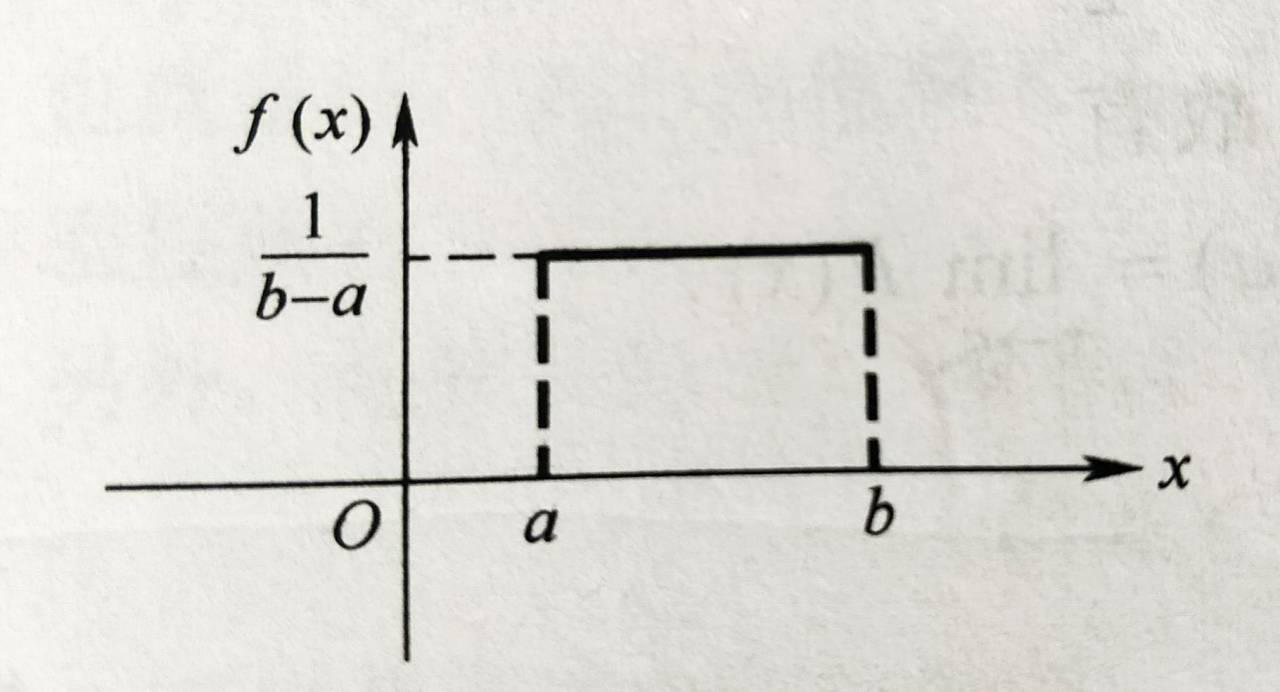
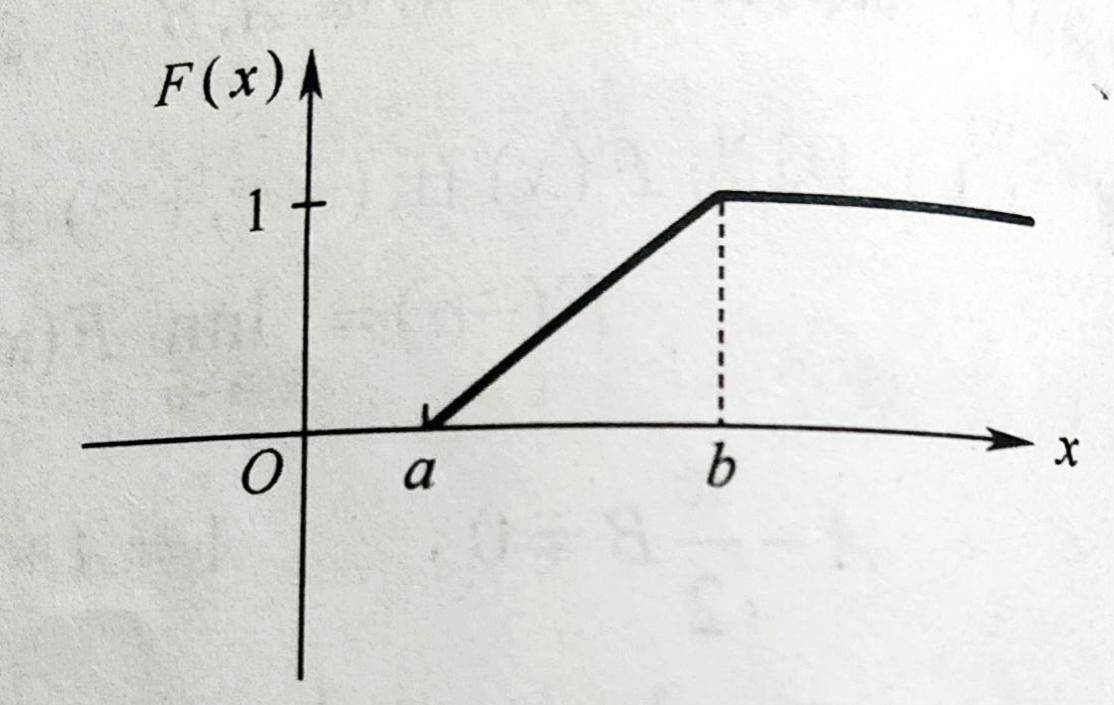
指数分布
若随机变量X的概率密度函数为:
X的分布函数为:
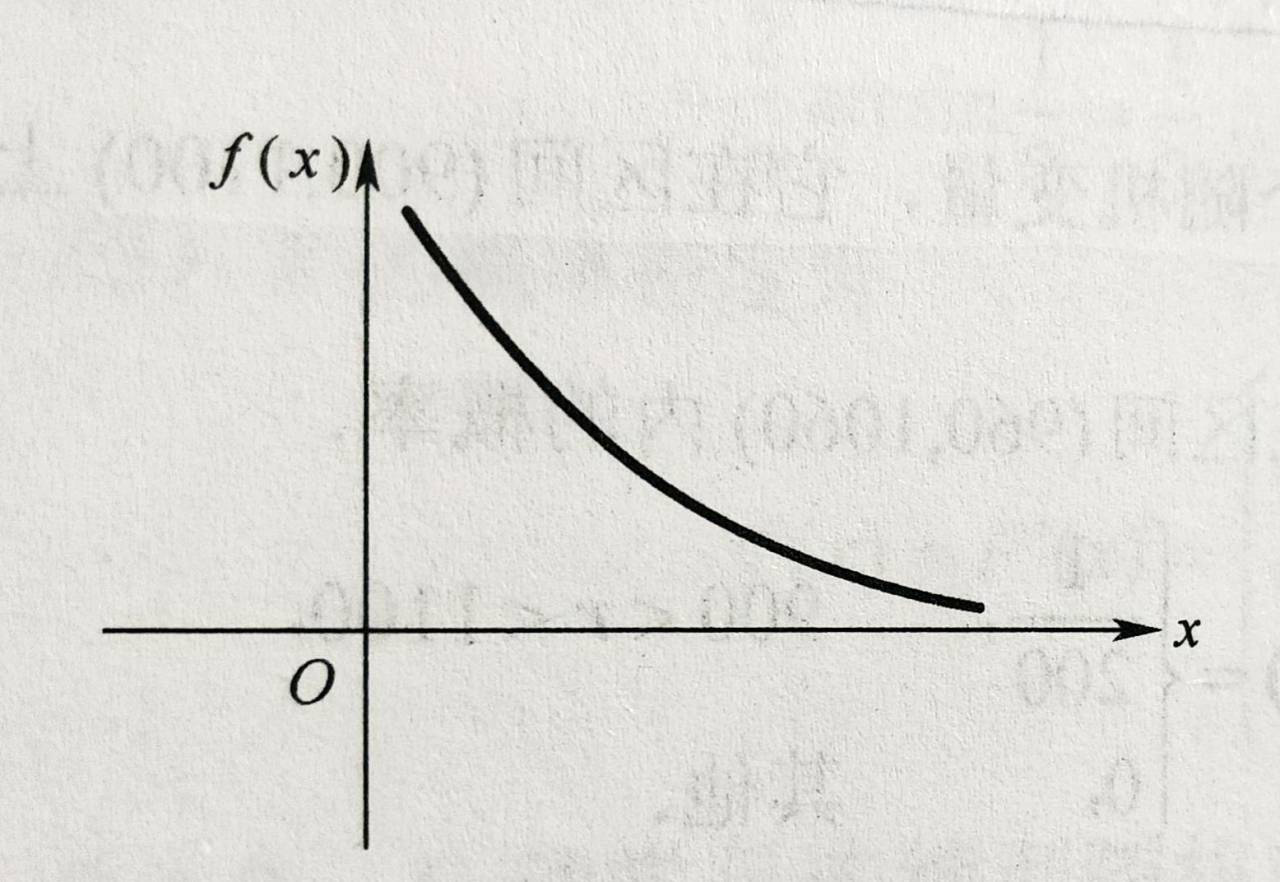
正态分布
若随机变量X的概率密度函数为: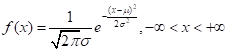
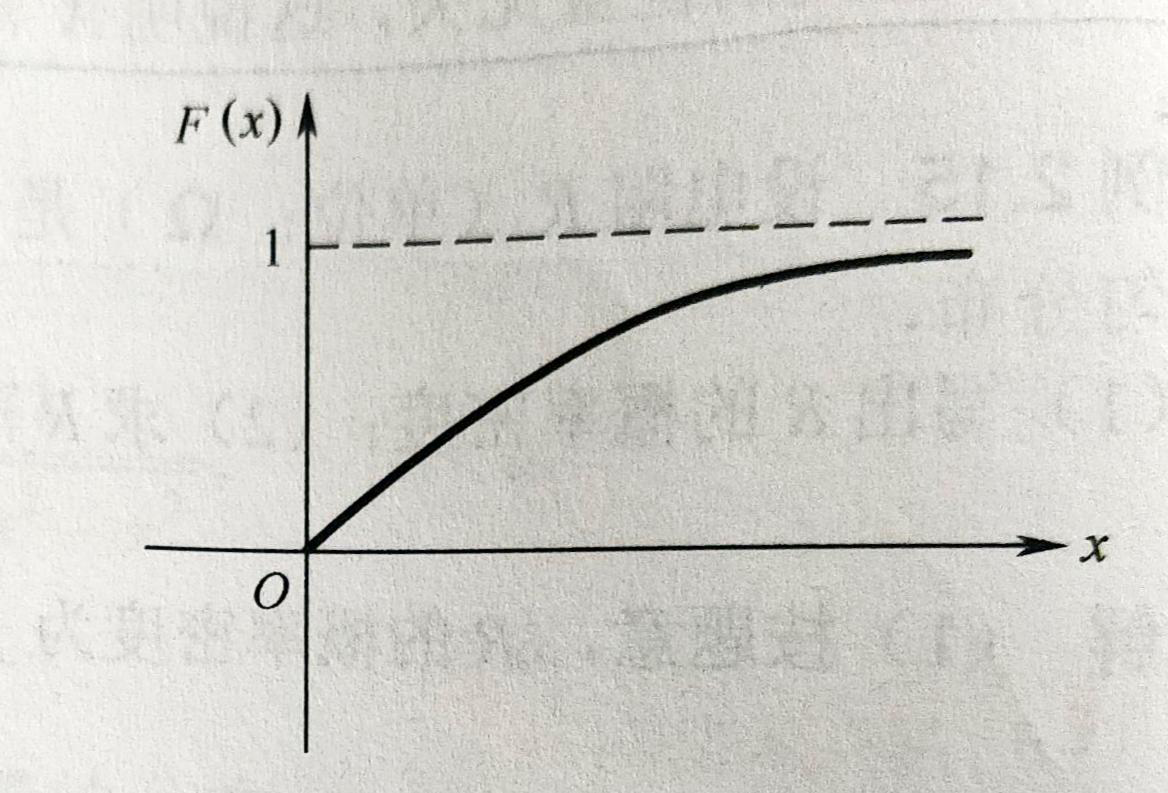
X的分布函数为: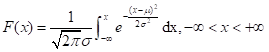
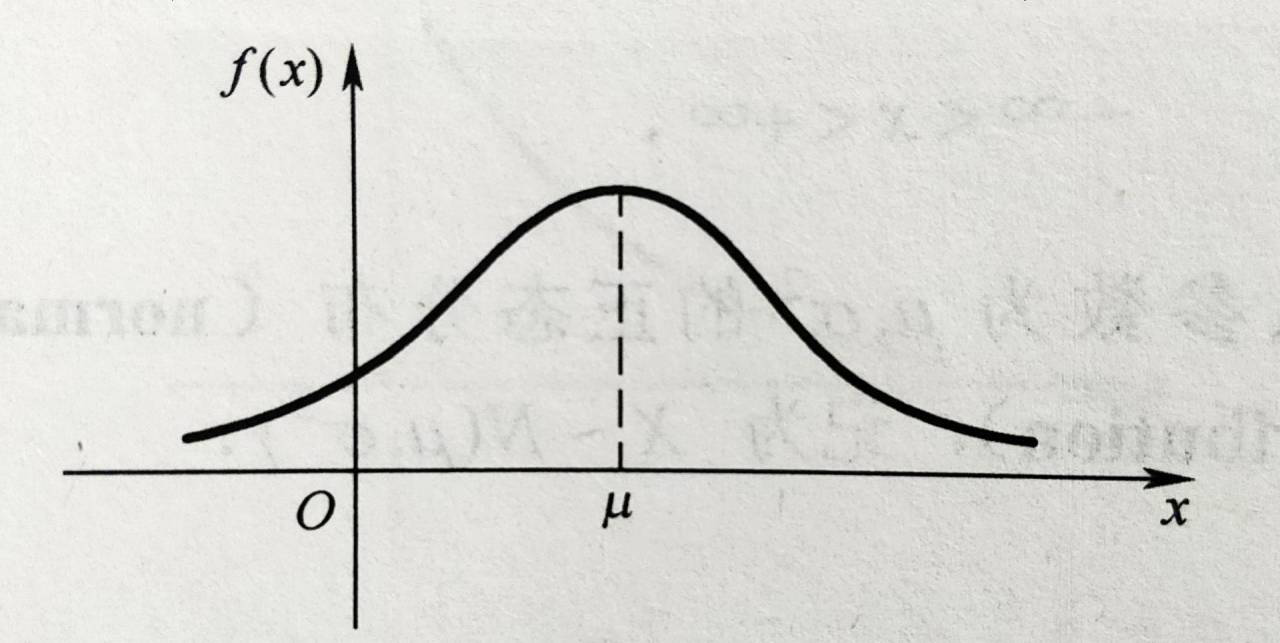

概率密度f(x)具有以下性质:
- f(x)的图形关于x=μ对称
- x=μ时,f(x)取得最大值
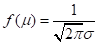
- 在x=μ+σ,μ-σ处有拐点
- 概率密度曲线y=f(x)以x轴为渐近线
正态分布的参数μ,σ有重要意义:
- 若固定σ,改变μ,则f(x)的图形沿x轴平行移动,而不改变形状。μ是反映分布的中心位置,称为位置参数
- 若固定μ,改变σ,由于f(x)的最大值为
 ,可知σ越小,最大值会越大,图形会变得“集中”,“高”,“瘦”。σ是反映分布的分散程度的,称为形状参数
,可知σ越小,最大值会越大,图形会变得“集中”,“高”,“瘦”。σ是反映分布的分散程度的,称为形状参数
标准正态分布
当μ=0,σ=1,则称X服从标准正态分布。
- 概率密度:
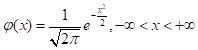
- 分布函数:
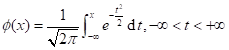 ,且
,且
- 若
 ,则
,则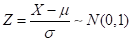
随机变量的分布函数
- 设X是一个随机变量,x是任意实数,则称函数F(x)=P(X<=x),为随机变量X的分布函数,也记为FX(x)。
- 随机变量X落在任意区间(x1,x2](x1<x2)内的概率为:P(x1<X<=x2)=P(X<=x2)-P(X<=x1)=F(x2)-F(x1)
分布函数F(x)基本性质:
- 0<=F(x)<=1
- F(x)是单调不减函数。即对任意x1<x2,有F(x1)<=F(x2)
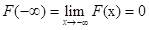 ,
,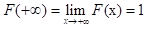
- F(x)是右连续的。(函数在该点的右极限存在且等于该点的函数值)
- 对于任意一个随机变量X,如果有X的分布函数F(x)在x=x0处连续,则P(X=x0)=0
离散型随机变量函数的分布
设P(X=xk)=pk,k=1,2,...,则由函数可列可加性得,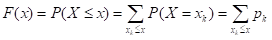 。(这里求和是对所有满足xk<=x的值求和)
。(这里求和是对所有满足xk<=x的值求和)
连续型随机变量函数的分布
设X为连续型随机变量,其概率密度为fX(x),求Y=g(X)的概率密度fY(y):
- 求出Y=g
- 由关系式fY(y)=F'Y(y)求出fY(y)