( ext{update 2019.8.18}) 由于本人将大部分精力花在了cnblogs上,而不是洛谷博客,评论区提出的一些问题直到今天才解决。
下面给出的Pollard Rho函数已给出散点图。关于(Millar Robin)算法的时间复杂度在我的博客应该有所备注。由于本人不擅长时间复杂度分析,如果对于时间复杂度有任何疑问,欢迎在下方指出。
1.1 问题的引入
给定一正整数(N in mathbb{N}^*),试快速找到它的一个因数。
很久很久以前,我们曾学过试除法来解决这个问题。很容易想到因数是成对称分布的:即(N)的所有因数可以被分成两块:([1,sqrt(N)])和([sqrt(N),N]).这个很容易想清楚,我们只需要把区间([1,sqrt(N)])扫一遍就可以了,此时试除法的时间复杂度为(O(sqrt(N))).
对于(N geqslant 10^{18})的数据,这个算法运行起来无意是非常糟糕的.我们希望有更快的算法,比如(O(1))级别的?
对于这样的算法,一个比较好的想法是去设计一个随机程序,随便猜一个因数.如果你运气好,这个程序的时间复杂度下限为(o(1)).但对于一个(N geqslant 10^{18})的数据,这个算法给出答案的概率是(frac{1}{1000000000000000000}).当然,如果在([1,sqrt(N)])里面猜,成功的可能性会更大.
那么,有没有更好的改进算法来提高我们猜的准确率呢?
2.1 用一个悖论来提高成功率
我们来考虑这样一种情况:在([1,1000])里面取一个数,取到我们想要的数(比如说,(42)),成功的概率是多少呢?显然是(frac{1}{1000}).
一个不行就取两个吧:随便在([1,1000])里面取两个数.我们想办法提高准确率,就取两个数的差值绝对值.也就是说,在([1,1000])里面任意选取两个数(i , j),问(|i-j|=42)的概率是多大?答案会扩大到(frac{1}{500})左右,也就是将近扩大一倍.机房的gql大佬给出了简证:(i)在([1,1000])里面取出一个正整数的概率是(100\%),而取出(j)满足(|i-j|=42)的概率差不多就是原来的一倍:(j)取(i-42)和(i+42)都是可以的.
这给了我们一点启发:这种"组合随机采样"的方法是不是可以大大提高准确率呢?
这个便是生日悖论的模型了.假如说一个班上有k个人,如果找到一个人的生日是4月2日,这个概率的确会相当低.但是如果单纯想找到两个生日相同的人,这个概率是不是会高一点呢?
可以暴力证明:如果是(k)个人生日互不相同,则概率为:(p=frac{365}{365}cdotfrac{364}{365}cdotfrac{363}{365}cdotdotscdotfrac{365-k+1}{365}) ,故生日有重复的现象的概率是:( ext{P}(k)=1-prodlimits_{i=1}^{k}{frac{365-i+1}{365}}).
我们随便取一个概率:当(P(k) geqslant frac{1}{2})时,解得(k gtrsim 23).这意味着一个有23个人组成的班级中,两个人在同一天生日的概率至少有(50\%)!当k取到60时,( ext{P}(k) approx 0.9999).这个数学模型和我们日常的经验严重不符.这也是"生日悖论"这个名字的由来.
3.1 随机算法的优化
生日悖论的实质是:由于采用"组合随机采样"的方法,满足答案的组合比单个个体要多一些.这样可以提高正确率.
我们不妨想一想:如何通过组合来提高正确率呢?有一个重要的想法是:最大公约数一定是某个数的约数.也就是说,(forall k in mathbb{N}^* , gcd(k,n)|n).只要选适当的k使得(gcd(k,n)>1)就可以求得一个约数(gcd(k,n)).这样的k数量还是蛮多的:k有若干个质因子,而每个质因子的倍数都是可行的.
我们不放选取一组数(x_1,x_2,x_3,dots,x_n),若有(gcd(|x_i-x_j|,N)>1),则称(gcd(|x_i-x_j|,N))是N的一个因子.早期的论文中有证明,需要选取的数的个数大约是(O(N^{frac{1}{4}})).但是,我们还需要解决储存方面的问题.如果(N=10^{18}),那么我们也需要取(10^4)个数.如果还要(O(n^2))来两两比较,时间复杂度又会弹回去.
3.2 Pollard Rho 和他的随机函数
我们不妨考虑构造一个伪随机数序列,然后取相邻的两项来求gcd.为了生成一串优秀的随机数,Pollard设计了这样一个函数:
(f(x)=(x^2+c)mod N)
其中c是一个随机的常数.
我们随便取一个(x_1),令(x_2=f(x_1)),(x_3=f(x_2)),(dots),(x_i=f(x_{i-1})).在一定的范围内,这个数列是基本随机的,可以取相邻两项作差求gcd.
生成伪随机数的方式有很多种.但是这个函数生成出来的伪随机数效果比较好.它的图像长这个样子:
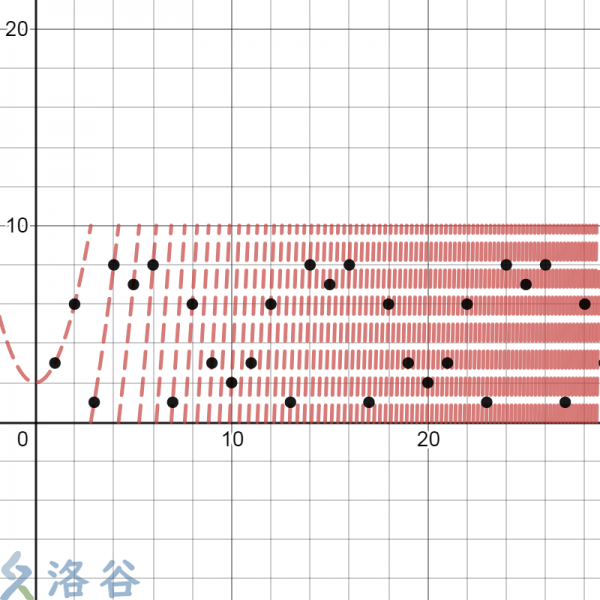
这里的函数为(f(x)=(x^2+2)mod 10)。图中的黑点为迭代(1,2,cdots,30)次得到的随机数。其实从这里很容易看出一个重复3次的循环节。
选取这个函数是自有道理的.有一种几何图形叫做曼德勃罗集,它是用(f(x)=x^2+c),然后带入复数,用上面讲到的方式进行迭代的.

↑曼德勃罗集.每个点的坐标代表一个复数(x_1),然后根据数列的发散速度对这个点染色.
这个图形和所谓的混沌系统有关.我猜大概是混沌这个性质保证了Pollard函数会生成一串优秀的伪随机数吧.
不过之所以叫伪随机数,是因为这个数列里面会包含有"死循环".
({1,8,11,8,11,8,11,dots})这个数列是(c=7,N=20,x_1=1)时得到的随机数列.这个数列会最终在8和11之间不断循环.循环节的产生不难理解:在模N意义下,整个函数的值域只能是({0,1,2,dots,N-1}).总有一天,函数在迭代的过程中会带入之前的值,得到相同的结果.
生成数列的轨迹很像一个希腊字母(
ho),所以整个算法的名字叫做Pollard Rho.
3.3 基于Floyd算法优化的Pollard Rho
为了判断环的存在,可以用一个简单的Floyd判圈算法,也就是"龟兔赛跑".
假设乌龟为(t),兔子为(r),初始时(t=r=1).假设兔子的速度是乌龟的一倍.
过了时间(i)后,(t=i,r=2i).此时两者得到的数列值(x_t=x_i,x_r=x_{2i}).
假设环的长度为(c),在环内恒有:(x_i=x_{i+c}).
如果龟兔"相遇",此时有:(x_r=x_t),也就是(x_i=x_{2i}=x_{i+kc}).此时两者路径之差正好是环长度的整数倍。
这样以来,我们得到了一套基于Floyd判圈算法的Pollard Rho 算法.
int f(int x,int c,int n)
{
return (x*x+c)%n;
}
int pollard_rho(int N)
{
int c=rand()%(N-1)+1;
int t=f(0,c,N),r=f(f(0,c,N),c,N);//两倍速跑
while(t!=r)
{
int d=gcd(abs(t-r),N);
if(d>1)
return d;
t=f(t,c,N),r=f(f(r,c,N),c,N);
}
return N;//没有找到,重新调整参数c
}
3.4 基于路径倍增和一个常数的优化
由于求(gcd)的时间复杂度是(O(log{N}))的,频繁地调用这个函数会导致算法变得异常慢.我们可以通过乘法累积来减少求gcd的次数.
显然的,如果(gcd(a,b)>1),则有(gcd(ac,b)>1),c是某个正整数.更近一步的,由欧几里得算法,我们有(gcd(a,b) = gcd(acmod b,b) >1). 我们可以把所有测试样本(|t-r|)在模N意义下乘起来,再做一次gcd.选取适当的相乘个数很重要.
我们不妨考虑倍增的思想:每次在路径( ho)上倍增地取一段([2^{k-1},2^k])的区间.将(2^{k-1})记为(l),(2^k)记为(r).取而代之的,我们每次取的gcd测试样本为(|x_i-x_l|),其中(l leqslant i leqslant r).我们每次积累的样本个数就是(2^{k-1})个,是倍增的了.这样可以在一定程度上避免在环上停留过久,或者取gcd的次数过繁的弊端.
当然,如果倍增次数过多,算法需要积累的样本就越多。我们可以规定一个倍增的上界。

↑(127=2^7-1),据推测应该是限制了倍增的上界。
一旦样本的长度超过了127,我们就结束这次积累,并求一次(gcd)。(127)这个数应该是有由来的。在最近一次学长考试讲解中,(128)似乎作为“不超过某个数的质数个数”出现在时间复杂度中。不过你也可以理解为,将"迭代7次"作为上界是实验得出的较优方案。如果有知道和(128)有关性质的大佬,欢迎在下方留言。
这样,我们就得到了一套完整的,基于路径倍增的Pollard Rho 算法.
inline ll PR(ll x)
{
ll s=0,t=0,c=1ll*rand()%(x-1)+1;
int stp=0,goal=1;
ll val=1;
for(goal=1;;goal<<=1,s=t,val=1)
{
for(stp=1;stp<=goal;++stp)
{
t=f(t,c,x);
val=(lll)val*abs(t-s)%x;
if((stp%127)==0)
{
ll d=gcd(val,x);
if(d>1)
return d;
}
}
ll d=gcd(val,x);
if(d>1)
return d;
}
}
这个代码不一定是最好的,还可以有相当多的优化.不过至少它足够通过部分毒瘤数据了.
4.1 例题
这个问题还需要一个Miller Rabin测试来快速测定质数.
对于一个数(n),我们首先用Miller Rabin快速判定一下这个数是不是质数.如果是则直接返回,否则就用Pollard Rho 找一个因子p.
将n中的因子p全部删去,再递归地分解新的n和p.
可以用一个全局变量max_factor记录一下n最大的因子,在递归分解的时候就可以把没必要的操作"剪枝"掉.
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define RP(i,a,b) for(register int i=a;i<=b;++i)
#define DRP(i,a,b) for(register int i=a;i>=b;--i)
#define fre(z) freopen(z".in","r",stdin),freopen(z".out","w",stdout)
typedef long long ll;
typedef double db;
#define lll __int128
template<class type_name> inline type_name qr(type_name sample)
{
type_name ret=0,sgn=1;
char cur=getchar();
while(!isdigit(cur))
sgn=(cur=='-'?-1:1),cur=getchar();
while(isdigit(cur))
ret=(ret<<1)+(ret<<3)+cur-'0',cur=getchar();
return sgn==-1?-ret:ret;
}
ll max_factor;
inline ll gcd(ll a,ll b)
{
if(b==0)
return a;
return gcd(b,a%b);
}
inline ll qp(ll x,ll p,ll mod)
{
ll ans=1;
while(p)
{
if(p&1)
ans=(lll)ans*x%mod;
x=(lll)x*x%mod;
p>>=1;
}
return ans;
}
inline bool mr(ll x,ll b)
{
ll k=x-1;
while(k)
{
ll cur=qp(b,k,x);
if(cur!=1 && cur!=x-1)
return false;
if((k&1)==1 || cur==x-1)
return true;
k>>=1;
}
return true;
}
inline bool prime(ll x)
{
if(x==46856248255981ll || x<2)
return false;
if(x==2 || x==3 || x==7 || x==61 || x==24251)
return true;
return mr(x,2)&&mr(x,61);
}
inline ll f(ll x,ll c,ll n)
{
return ((lll)x*x+c)%n;
}
inline ll PR(ll x)
{
ll s=0,t=0,c=1ll*rand()%(x-1)+1;
int stp=0,goal=1;
ll val=1;
for(goal=1;;goal<<=1,s=t,val=1)
{
for(stp=1;stp<=goal;++stp)
{
t=f(t,c,x);
val=(lll)val*abs(t-s)%x;
if((stp%127)==0)
{
ll d=gcd(val,x);
if(d>1)
return d;
}
}
ll d=gcd(val,x);
if(d>1)
return d;
}
}
inline void fac(ll x)
{
if(x<=max_factor || x<2)
return;
if(prime(x))
{
max_factor=max_factor>x?max_factor:x;
return;
}
ll p=x;
while(p>=x)
p=PR(x);
while((x%p)==0)
x/=p;
fac(x),fac(p);
}
int main()
{
int T=qr(1);
while(T--)
{
srand((unsigned)time(NULL));
ll n=qr(1ll);
max_factor=0;
fac(n);
if(max_factor==n)
puts("Prime");
else
printf("%lld
",max_factor);
}
return 0;
}