简述
容斥原理是组合数学中很常用的方法。其主要思想在于,把一个不好解决的问题,花费时间,变成一个好解决的问题。容斥有很多种。
很多容斥的本质其实是反演。
一般容斥
一般容斥的本质是二项式反演,它是通过二项式反演转化两个问题
常见的形式是交与并的转化,通过某些数学变形,也可以得到 min-max 容斥。
算法讲解
小学都学过。略。
例题
T1 CF1400G
咕咕咕。
莫比乌斯容斥
莫比乌斯容斥的本质是莫比乌斯反演,它是通过莫比乌斯反演转化两个问题
算法讲解
我们知道莫比乌斯函数有一个性质: (sumlimits_{d|n} mu(d)=[n=1])
根据这条性质,我们写出一个类似筛的东西:一个数组,初始都是 (0)。 第 (i) 轮,将 (i) 的倍数都加上 (mu(i))。
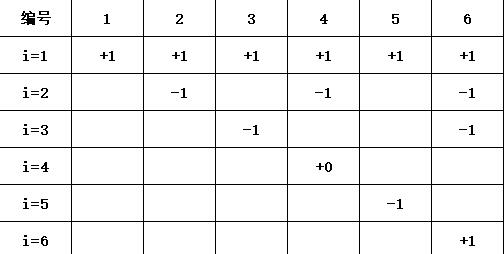
(n) 轮之后,显然只有第一个位置还剩一个 (1),其它都变成了 (0)。好好理解下这个表,然后往下看。
那么,假设现在我们要求 (n=1) 时的答案,但是我们方便求的只有 (n) 的倍数的答案和,考虑转化:设 (f(x)) 表示 (n) 恰好为 (x) 的答案,(F(x)) 表示 (n) 为 (x) 的倍数的答案和,即 (sumlimits_{d|n} f(n))。
考虑式子 (sumlimits_{i=1}^{n} mu(i)F(i)),很明显它 (=sumlimits_{i=1}^{n}sumlimits_{i|j} mu(i)f(j))
考虑每个 (f(i)) 被算了多少次,变为:
(sumlimits_{j=1}^{n} f(j) sumlimits_{i|j} mu(i)=sumlimits_{j=1}^{n} f(j) [j=1]=f(1))
正好就是"(n) 恰好为 (1)"的答案。
也可以联系上面那个表来理解:我们给每一列带上一个 (f(i)) 的权值,(F(i)) 就是 (i) 的倍数列的和。然后我们把所有的 (F(i)*mu(i)) 加起来, 根据上面那个表,只会在第一列剩下一个“1”。又因为我们带了一个 (f(i)) 的权,相当于剩下的就是 (f(1)) 了。
所以,莫比乌斯容斥的解题步骤:
- 找到“(n)”与“(f)”,并且答案就是 (n=1) 的答案。
- 求 (n) 的倍数的方案和(一般这一步比较simple)
例题
T1. CF 439E
给定 (q) 个询问,每次给定 (n,k) ,问有多少种方法,把 (n) 分成 (k) 个数相加,并且 所有数 的 (gcd) 为 (1)(即:允许有部分的 (gcd) 不为 (1) ,比如 (n=20,k=3) 时,({2,3,15}) 是合法的一组拆分)
(q,nle 10^5,kle n)
题解
设 “(k) 个数的 (gcd)” 这个整体为 “(n)”,那这题的答案就是 (n=1) 的方案数。
设 (f(i)) 表示:(k) 个数的 (gcd=i) 的方案数,(F(i)) 就是 (k) 个数的 (gcd) 是 (i) 的倍数的方案数。
(F(i)) 好求。显然,此时 (i) 是 (n) 的因数((k) 个数都是 (i) 的倍数,所以它们加起来, (n) 也是 (i) 的倍数)。如果不是,那么 (F(i)=0)
然后所有数都是 (i) 的倍数的划分方案,我们可以把 (i) 个数并成一块,然后有 (n/i) 个块,任意划分成 (k) 个部分,求方案数。隔板法得它等于 (C_{n/i-1}^{k-1})。
反演回去即可。然而,枚举 (i|n) 这一步是 (O(n sqrt{n})) 的,于是总复杂度 (O(nsqrt{n}))
T2. CF 900D
同样是求划分的问题。相当于在 (T1) 的基础上:
- 去掉 (k) 的限制
- 一组询问,范围改成 (nle 10^9),答案模 (10^9+7)
- 给定了参数 (y),划分完所有数的 (gcd=y) (而不是等于 (1))
题解
所有数 (gcd=y),相当于所有数除以 (y) 之后 (gcd=1)。
然后没有了 (k) 的限制,相当于所有的隔板随便选/不选。不隔板了,答案直接是 (2^{n/y-1})。
假设有 (n) 个隔板,答案为 (2^{n})。然后,(n) 个数不限个数划分,每个数都是 (y) 的倍数,方案数就是 (2^{n/y-1})。
然后要注意的是,(nle 10^9),只有一部分 (mu) 可以筛出来,超过范围的就只好暴力算了。
讲道理复杂度过不去,但是的确能过。
T3. CF1036F
(T) 组询问,每次询问 ([2,n]) 中有多少好数。一个数 (x) 是“好数”,那么不存在任何一个 (k) 使得 (sqrt[k]{x}) 是整数。
(Tle 10^5,xle 10^{18})。
题解
一个数是“好数”,那么它分解质因数后,所有指数的 (gcd=1)
然后我们考虑所有指数的 (gcd) 是 (k) 的倍数怎么算。很显然,这个方案数就是 (lfloor sqrt[k]{x} floor) 。
然后 (k) 大概枚举到 (60,70) 就够了。
然后卡亿点点常数就过了