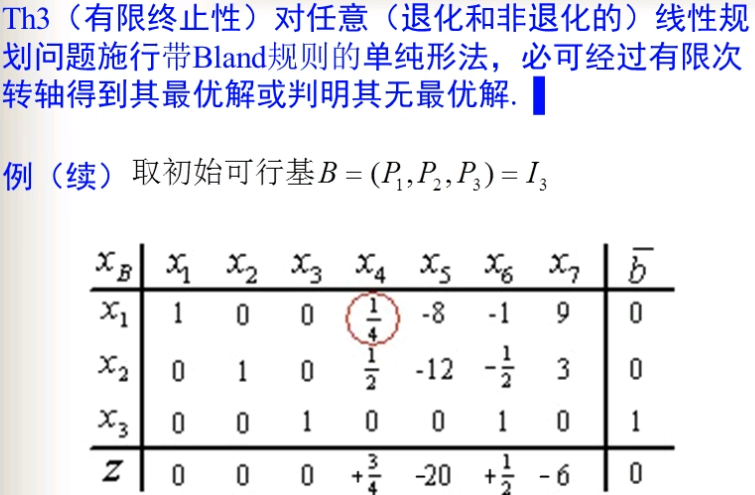
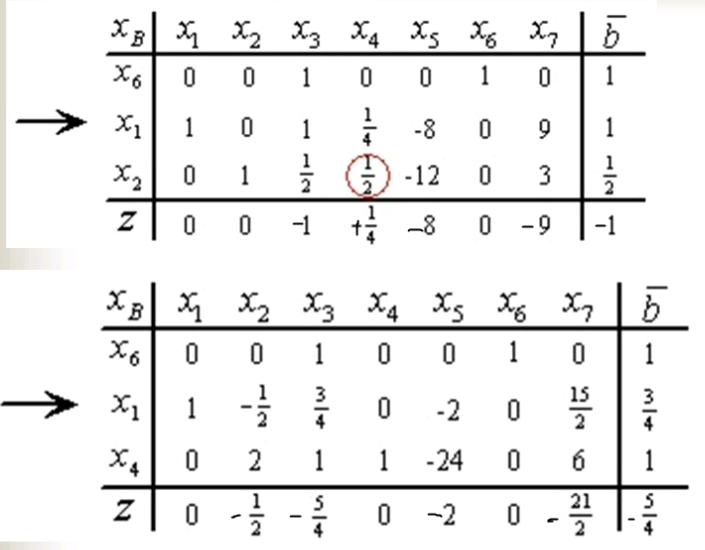
根据基可以写出对应的典式,根据典式可以写出对应的单纯形表。反之,根据单纯形表,也可以写出典式。典式当中的非基变量移到等号的右侧,则可以得到典式的等价形式;
如下图所示。当所有非基变量的检验数都是负数时,那我们来看下目标函数等价形式的中的rjxj项,如下图所示。

上图中,圈主部分中的xj只要不取零(xj>=0),那么结果都会大于等于z0, 只有当所有非基变量的取值为零时,才等于z0;只有所有非基变量取值为零,
此时的可行解才是该问题的最优解,而所有非基变量取值为零只有一种取法,所以该问题有唯一的最优解。当某个非基变量的检验数等于零,假设xk的检验数等于零,
我们就将xk作为如基变量,然后按照最小比值原则来选取出基变量,从而可以选定枢轴元,并进一步的转轴。

由此,可发现转轴前的目标函数值,以及转轴后的目标函数值是一样的;而且转轴前的检验数<=0,那么转轴后的检验数也<=0;这就说明前后的两个表格对应的基可行解都是该问题的最优解;那么与这两个最优解作为端点做端组合,也即是说以这两个端点作为端点做直线段,直线段上的所有点都是标准形的最优解,这就说明了该问题有无穷多最优解。
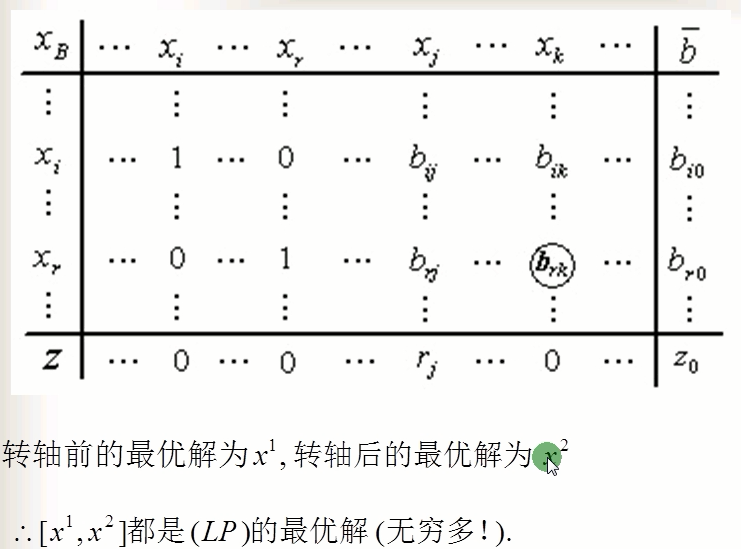


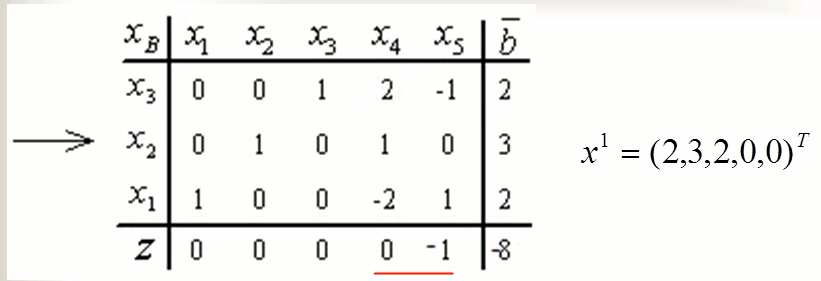
由上图可知,因为上述表格中的所有非基变量对应的检验数都是<=0的,所以,上述表格中看到的基可行解就是标准形的一个最优解,表格对应的基可行解中的一个为x1;
x1所对应的目标函数值是-8;但是由于非基变量x4对应的检验数是0,而不是小于零的数;所以,根据前面的介绍可知,该问题的最优解绝不止只有x1这一个向量,
一定还有其他的。
找到另外的最优解的方法就是转轴,现在只有x4是非基变量了,然后用最小比值原则来确定出基变量,然后x3就出来变成非基向量了,转轴后,得到下图2处单纯形表。

在新的单纯形表中,检验数依然是小于等于零的,观察到的基可行基是x2=(4,2,0,1,0)的转置,其依然是标准形的最优解。两个表格右下角的目标函数值全都是一样的。
因为,x1,x2都是标准形的最优解,现在用这两个点为端点做直线段/同组合。
由此得到的向量都是标准型的最优解,最优值是-8.
要想得到原问题的最优解,只需要,在这个解向量当中,把原问题中没有出现的变量x3,x4,x5的取值抹掉即可,如下图抹掉。

保留下来的向量就是原问题的最优解。 注意原问题的目标函数值和标准型的目标函数值符号是不一样的,一个求最大,一个求最小,他们的值是相反的。

可看到,此问题确实有无穷多最优解。
其实这个问题有两个决策变量,所以完全可以用图解法来进行求解。
如下图所示, x1=(2,3),x2=(4,2),就是刚才求解过程最后两个单纯形表所对应的原问题的两个最优解,以二者为端点的直线段就是线图中的红色线段。
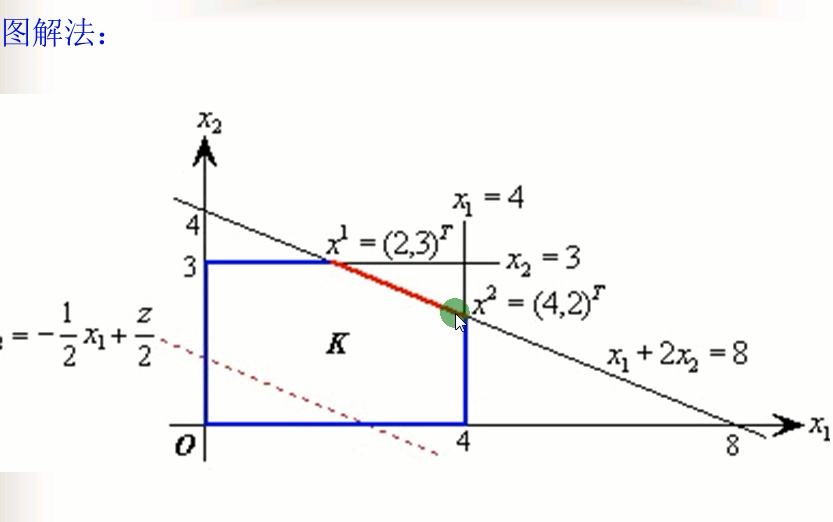
红线段上的每个点都是该问题的最优解,他们对应的函数值都是8,由此可看出该问题确实是无穷多解。
2.使用单纯性法,可否在有限步内,判明一个问题是否有最优解。

非退化的基可行解:首先某个向量是一个标准型的一个基可行解,如果此基可行解的所有基变量的取值都是正值,则这个基可行解称为非退化的基可行解;
否则就是一个退化的基可行解。
假设某个标准形式的线性规划问题,有4个变量,其中有两个等式约束,这就告诉我们基变量和非基变量都有两个。假设图中的α是这个问题的一个基可行解,从上图中可以观察到x3,x4一定是非基变量,x1,x2的值都是正值,所以这个α就是非退化的基可行解。对应的图中的β则是退化的基可行解。
非退化的线性规划问题:如果一个线性规划问题的所有的基可行解都是非退化的,那么这个线性规划问题就称为非退化的线性规划问题;如果一个线性规划问题的某一个或多个基可行解是退化的,那么就称为退化的线性规划问题。





上图,e.g.:x1,x2都为非基变量,检验数分别为3和5,那就把x1作为入基变量;而选取出基变量依然用最小比值原则来选定。如果发现最小比值不止一行时,则选择位置靠上的
变量作为出基变量。由此确定枢轴元,并进行转轴;转轴的方法和前面的方法时一致的;这样的话就可以避免死循环;进而也就有了下面的结论Th3。