第三章主要是三维空间刚体运动描述方式:旋转矩阵,变换矩阵,四元数、欧拉角以及Eigen库的使用。由于本周时间比较紧,看的比较粗略,如有错误还请不吝赐教,不胜感激。
下面记录以散碎的知识点为主,日后在行整理。
1.两个向量的外积a X b可以看做一个矩阵和向量的乘法。其中a变为一个反对称矩阵。 外积表示向量的旋转
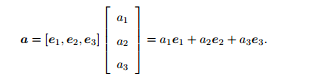 基坐标表示
基坐标表示
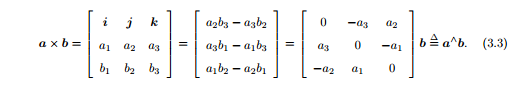
2. 伟大的欧拉
(1)一个向量在机器人坐标系下的坐标到世界坐标系下坐标的转换可以有一个旋转加一个平移组成。(刚体运动)
(2)旋转矩阵。(公式后面补)其各分量两个坐标系基的内积。
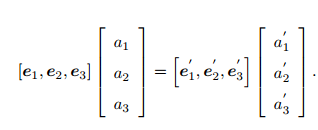 一个向量a在旋转后刚体不变,坐标描述变了
一个向量a在旋转后刚体不变,坐标描述变了
同时左乘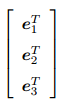
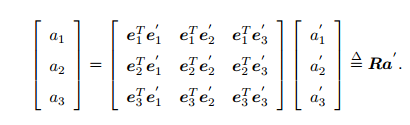
R就是旋转矩阵。描述相机旋转。为正交阵,其逆就是转置
SO(N) 特殊正交群 。 n维。这个集合有n维空间的旋转矩阵构成。
(3)变换矩阵与齐次坐标。
 a'为变换后的矩阵。
a'为变换后的矩阵。

在三维向量末尾添加1,变成四维向量,即为齐次坐标。然后根据a'=Ra+t,得出变换矩阵。
SE(N) 特殊欧氏群。 左上角为旋转,右侧平移向量,右下角为1;。
3.旋转向量和欧拉角
(1) 问题 :SO(3)的旋转矩阵有9个量,但一次旋转只有3个自由度,因此该表达方式冗余。变换矩阵16个量表示6个自由度。
旋转矩阵必须是正交矩阵,行列式为1.自身带有约束,估计优化有困难。
解决:因此提出用一个旋转轴和一个旋转角刻画变换。
一个三维向量方向与旋转轴一致,长度为旋转角,该向量即为旋转向量。再用一个三维向量表示平移,正好对应变换矩阵的六维。
罗德里格斯公式:
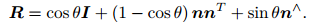
描述了R旋转矩阵与旋转向量表示法θn 之间的关系
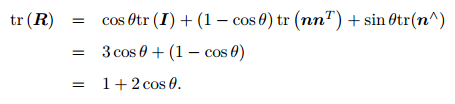 后面会用到
后面会用到
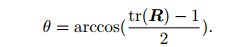
(2)欧拉角
yaw- pitch- roll;
偏航角,俯仰角,滚转角
z轴 y轴 x轴
万向锁问题(待学,后面附教学视频链接),即奇异性问题。
适用于2D场合,只用其中一个定位。
4.四元数
利用复数域乘法法则的性质。基础性质略
某个旋转绕单位向量n=[nx,ny,nx]T 进行角度为θ旋转,四元数形式为 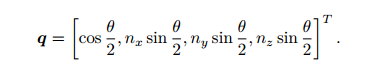
反求旋转轴和夹角(证明过程先略过)
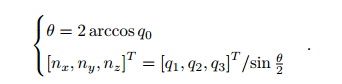
/* p' = qpq-1 其中p为空间中一个点,用虚四元数表示。
取出p'的虚部就可得到旋转后点的坐标。*/
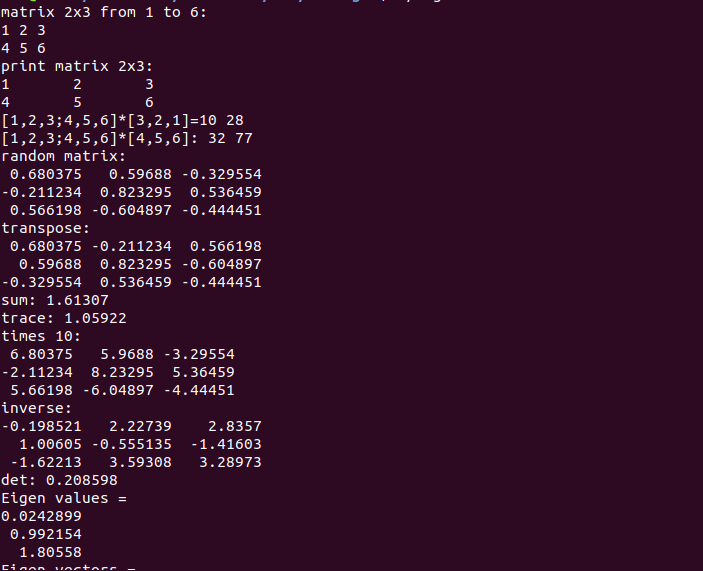
eigen库使用:
#include <iostream> using namespace std; #include <ctime> // Eigen 核心部分 #include <Eigen/Core> // 稠密矩阵的代数运算(逆,特征值等) #include <Eigen/Dense> using namespace Eigen; #define MATRIX_SIZE 50 /**************************** * 本程序演示了 Eigen 基本类型的使用 ****************************/ int main(int argc, char **argv) { // Eigen 中所有向量和矩阵都是Eigen::Matrix,它是一个模板类。它的前三个参数为:数据类型,行,列 // 声明一个2*3的float矩阵 Matrix<float, 2, 3> matrix_23; // 同时,Eigen 通过 typedef 提供了许多内置类型,不过底层仍是Eigen::Matrix // 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>,即三维向量 Vector3d v_3d; // 这是一样的 Matrix<float, 3, 1> vd_3d; // Matrix3d 实质上是 Eigen::Matrix<double, 3, 3> Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零 // 如果不确定矩阵大小,可以使用动态大小的矩阵 Matrix<double, Dynamic, Dynamic> matrix_dynamic; // 更简单的 MatrixXd matrix_x; // 这种类型还有很多,我们不一一列举 // 下面是对Eigen阵的操作 // 输入数据(初始化) matrix_23 << 1, 2, 3, 4, 5, 6; // 输出 cout << "matrix 2x3 from 1 to 6: " << matrix_23 << endl; // 用()访问矩阵中的元素 cout << "print matrix 2x3: " << endl; for (int i = 0; i < 2; i++) { for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << " "; cout << endl; } // 矩阵和向量相乘(实际上仍是矩阵和矩阵) v_3d << 3, 2, 1; vd_3d << 4, 5, 6; // 但是在Eigen里你不能混合两种不同类型的矩阵,像这样是错的 // Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d; // 应该显式转换 Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d; cout << "[1,2,3;4,5,6]*[3,2,1]=" << result.transpose() << endl; Matrix<float, 2, 1> result2 = matrix_23 * vd_3d; cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl; // 同样你不能搞错矩阵的维度 // 试着取消下面的注释,看看Eigen会报什么错 // Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d; // 一些矩阵运算 // 四则运算就不演示了,直接用+-*/即可。 matrix_33 = Matrix3d::Random(); // 随机数矩阵 cout << "random matrix: " << matrix_33 << endl; cout << "transpose: " << matrix_33.transpose() << endl; // 转置 cout << "sum: " << matrix_33.sum() << endl; // 各元素和 cout << "trace: " << matrix_33.trace() << endl; // 迹 cout << "times 10: " << 10 * matrix_33 << endl; // 数乘 cout << "inverse: " << matrix_33.inverse() << endl; // 逆 cout << "det: " << matrix_33.determinant() << endl; // 行列式 // 特征值 // 实对称矩阵可以保证对角化成功 SelfAdjointEigenSolver<Matrix3d> eigen_solver(matrix_33.transpose() * matrix_33); cout << "Eigen values = " << eigen_solver.eigenvalues() << endl; cout << "Eigen vectors = " << eigen_solver.eigenvectors() << endl; // 解方程 // 我们求解 matrix_NN * x = v_Nd 这个方程 // N的大小在前边的宏里定义,它由随机数生成 // 直接求逆自然是最直接的,但是求逆运算量大 Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE); matrix_NN = matrix_NN * matrix_NN.transpose(); // 保证半正定 Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1); clock_t time_stt = clock(); // 计时 // 直接求逆 Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd; cout << "time of normal inverse is " << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl; cout << "x = " << x.transpose() << endl; // 通常用矩阵分解来求,例如QR分解,速度会快很多 time_stt = clock(); x = matrix_NN.colPivHouseholderQr().solve(v_Nd); cout << "time of Qr decomposition is " << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl; cout << "x = " << x.transpose() << endl; // 对于正定矩阵,还可以用cholesky分解来解方程 time_stt = clock(); x = matrix_NN.ldlt().solve(v_Nd); cout << "time of ldlt decomposition is " << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl; cout << "x = " << x.transpose() << endl; return 0; }