主席树
是什么
- 它可以看作是多棵权值线段树,但它所占的空间很小!!!
- 具体不易解释,可以先往后面的内容浏览。
为什么要用它
- 对于一棵权值线段树,我们要往里面加入
n
n
n个数。容易知道,每加入一个数就会更新一遍线段树。
- 当我们想要知道每次更新后的权值线段树的状态时,如果我们直接用
n
n
n棵线段树,空间一般情况都会爆炸,于是这树我们要用到可持久化线段树——主席树。
- 假设有这么一串数:
2
,
4
,
2
,
3
2,4,2,3
2,4,2,3
- 每次更新后的状态如果都用一棵普通权值线段树表示的话,是这样的:
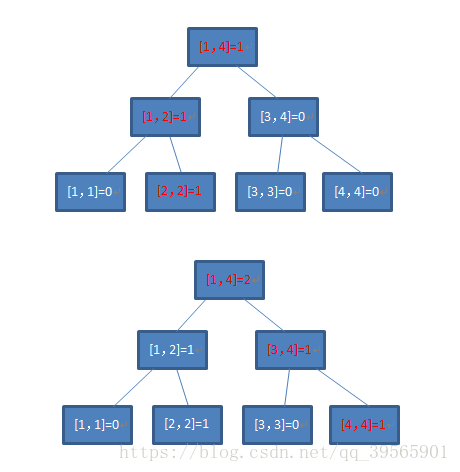
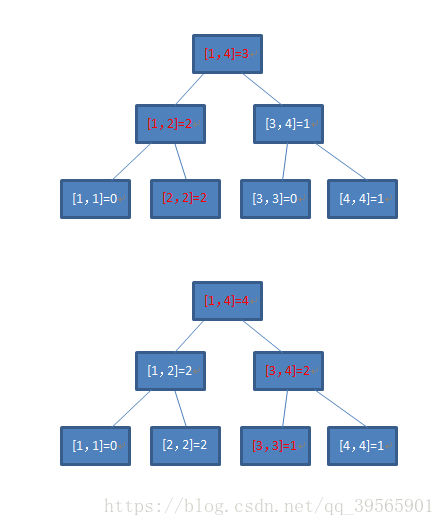
- 图中红色的节点代表它的值相比上一次修改后的值发生了变化。
- 在这里,我们不难发现,每次修改只会有添加的值到根节点的一条链上的值发生了变化,而其它的节点和上次修改结束后的都是一样的。
- 既然如此,我们为什么要每次新建一棵权值线段树呢?每次新建一条链不就好了吗?
先看看它究竟长什么样
- 注意,前方超高能预警!!!
- 白色字体为一棵空的树,
- 红色为第一次添加的节点,
- 紫色为第二次添加的节点,
- 绿色为第三次添加的节点,
- 棕色为第四次添加的节点。
- (为了画图好看,左右子树的位置可能相反,也就是可能左子树在右边,右子树在左边,分辨左右子树应看它们的区间所对应的值)
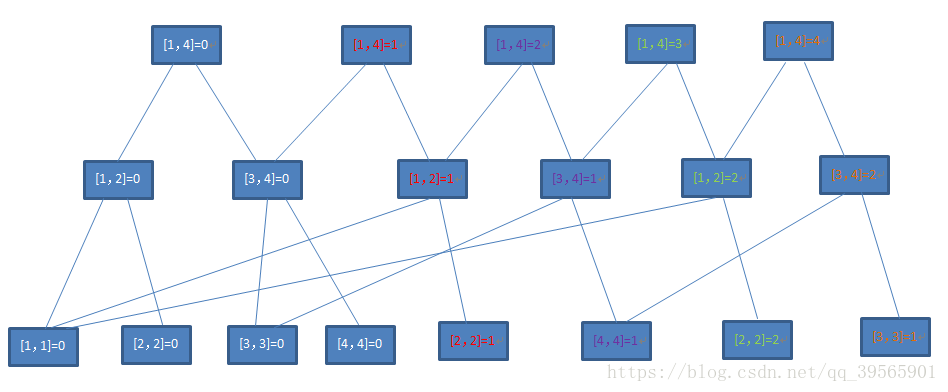
- 是不是特别震撼!!!现在的你是不是目瞪口呆!!!
怎么实现
- 首先我们要建立一棵没有值的权值线段树,如上图白色的地方。
- 修改时每到一个节点,判断要修改的值是在左子树还是右子树,新建将要修改的值所在的子节点,而另一边直接连向上一次修改的对应节点。
- 同时要记录每次修改的对应根节点编号。
- 注意:主席树的节点编号不一定满足
v
v
v的左子树为
v
∗
2
v*2
v∗2和右儿子为
v
∗
2
+
1
v*2+1
v∗2+1,所以必须用数组记录左右节点的编号。
- 举例:
- 如当前要修改
2
2
2,递归到区间
[
1
,
4
]
[1,4]
[1,4]时,
2
2
2在左儿子中,所以新建一个节点
[
1
,
2
]
[1,2]
[1,2]为当前的左儿子,而右儿子就为上一次修改完的区间
[
1
,
4
]
[1,4]
[1,4]的右儿子。
void make(int v,int l,int r)
{
if(l==r)
{
f[v].sum=0;
if(v>num) num=v;
return;
}
else
{
int mid=(l+r)/2;
f[v].l=v*2,f[v].r=v*2+1;
make(v*2,l,mid);
make(v*2+1,mid+1,r);
}
}
void add(int v,int v1,int l,int r,int x)
{
if(l==r)
{
f[v1].sum++;
return;
}
else
{
int mid=(l+r)/2;
if(x<=mid)
{
f[v1].l=++num;
f[v1].r=f[v].r;
add(f[v].l,f[v1].l,l,mid,x);
}
else
{
f[v1].l=f[v].l;
f[v1].r=++num;
add(f[v].r,f[v1].r,mid+1,r,x);
}
f[v1].sum=f[f[v1].l].sum+f[f[v1].r].sum;
}
}
root[0]=1;
make(1,1,n);
for(i=1;i<=n;i++)
{
root[i]=++num;
add(root[i-1],root[i],1,n,a[i]);
}
基本用处
- 求一个序列中,第
x
x
x个数到第
y
y
y个数中的第
k
k
k小值。
- 和权值线段树求第
k
k
k小值类似,每次从
x
−
1
x-1
x−1和
y
y
y的根节点开始往下递归。
- 每次的个数即为
y
y
y树中对应个数减去
x
−
1
x-1
x−1树中对应个数的值。
int find(int v,int v1,int l,int r,int k)
{
if(l==r) return l;
else
{
int mid=(l+r)/2,s1=f[f[v1].l].sum-f[f[v].l].sum,s2=f[f[v1].r].sum-f[f[v].r].sum;
if(s1>=k) return find(f[v].l,f[v1].l,l,mid,k);
else return find(f[v].r,f[v1].r,mid+1,r,k-s1);
}
}
for(i=1;i<=q;i++)
{
scanf("%d%d%d",&x,&y,&k);
printf("%d\n",find(root[x-1],root[y],1,n,k));
}
例题


