第三节–k近邻算法
k近邻法(k-nearest neighbor,KNN)是一种基本分类与回归方法.k近邻法的输入为实例的特征变量,对应于特征空间的点,输出为实例的类别,可以取多类.k近邻法假设给定一个训练数据集,其中的实例类别已定,分类时,对新的实例,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预测.因此,k近邻法不具有显式的学习过程,k近邻法实际上利用训练数据集对特征向量空间进行划分,并作为其分类的"模型".k值的选择,距离度量及分类决策规则是k近邻法的三个基本要素
首先叙述k近邻算法,然后讨论k近邻法的模型及三个基本要素,最后讲述k近邻法的一个实现方法–kd树
一.k近邻算法
k近邻算法简单,直观:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多树属于某个类,就把该输入实例分为这个类
输入:训练数据集
其中,为实例的特征向量,为实例的类别,;实例特征向量x
输出:实例x所属的类y
- 根据给定的距离度量,在训练集T中找出与x最近邻的k个点,涵盖这k个点的x的邻域记作为
- 在中根据分类决策规则(如多数表决)决定x的类别y:
其中I为指示函数,即当时I为1,否则I为0
k近邻法的特殊情况是k=1的情形,称为最近邻算法,对于输入的实例点(特征向量)x,最近邻法将训练数据集中与x最近邻点的类作为x的类
k近邻法没有显式的学习过程
二.k近邻模型
k近邻法使用的模型实际上对应于对特征空间的划分,模型由三个基本要素—距离度量,k值的选择和分类决策规则决定
1.模型
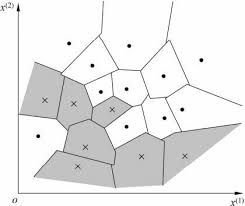
k近邻法中,当训练集,距离度量(如欧式距离),k值及分类决策规则(如多数表决)确定后.对于任何一个新的输入实例,它所属的类唯一地确定.这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类,这一事实从最近邻算法中可以看得很清楚
特征空间中,对每个训练实例点,距离该点比其他点更近的所有点组成一个区域,叫作单元(cell).每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分,最近邻法将实例的类作为其单元中所有点的类标记(class label).这样,每个单元的实例点的类别是确定的
from IPython.display import Image
Image(filename="./data/3_1.png",width=500)
2.距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映.k近邻模型的特征空间一般是n维实数向量空间.使用的距离是欧式距离,但也可以是其他距离.如更一般的距离( distance)或Minkowski距离(Minkowski distance)
设特征空间是n维实数向量空间,,的距离定义为:
这里p≥1.当p=2时,称为欧式距离(Euclidean distance),即:
当p=1时,称为曼哈顿距离(Manhattan distance),即:
当时,称为闵式距离(Minkowski distance),它是各个坐标距离的最大值,即:
下图给出了二维空间中p取不同值时,与原点的距离为1(=1)的点的图片
Image(filename="./data/3_2.png",width=500)

下面的例子说明,由不同的距离度量所确定的最近邻点是不同的
实例1:已知二维空间的3个点,试求在p取不同值时,距离下的最近邻点
Image(filename="./data/3_3.png",width=500)

于是得到:p等于1或2时,是的最近邻点;p大于等于3时,是的最近邻点
3.k值的选择
k值的选择会对k近邻法的结果产生重大影响
如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,"学习"的近似误差(approximation error)会减小,只有与输入实例较近的训练实例才会对预测结果其作用,但缺点是"学习"的估计误差(estimation error)会增大,预测结果会近邻的实例点非常敏感.如果邻近的实例点恰巧是噪声.预测就会出错.换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合
如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大.这时与输入实例较远训练实例也会对预测其作用,使预测发生错误,k值的增大就意味着整体的模型变得简单
4.分类决策规则
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类
多数表决规则(majority voting rule)有如下解释:如果分类的损失函数为0-1损失函数,分类函数为:
那么误分类的概率是:
对给定的实例,其最近邻的k个训练实例点构成集合.如果涵盖的区域的类别是,那么误分类率是:
要使误分类率最小即检验风险最小,就要使最大,所以多数表决规则等价于经验风险最小化
三.k近邻法的实现:kd树
实现k近邻法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索.这点在特征空间的维数大及训练数据容量大时尤其必要
k近邻法最简单的实现方法是线性扫描(linear scan).这时要计算输入实例与每一个训练实例的距离.当训练集很大时,计算非常耗时,这种方法是不可行的
为了提高k近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数.kd树(kd tree)方法就是一种
1.构造kd树
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构.kd树是二叉树,表示对k维空间的一个划分(partition).构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间划分,构成一系列的k维超矩形区域.kd树的每个结点对应于一个k维矩形区域
构造kd树的方法如下:构造根结点,使根结点对应于k维空间中包含所有实例点的超矩形区域;通过下面的递归方法,不断地对k维空间进行切分,生成子结点,在超矩形区域(结点)上选择一个坐标轴和在此坐标轴上的一个切分点,确定一个超平面,这个超平面通过选定的切分点并垂直于选定的坐标轴.将当前超矩形区域切分为左右两个子区域(子结点);这时实例被分到两个子区域,这个过程直到子区域内没有实例时停止(终止时的结点为叶结点).在此过程中,将实例保存在相应的结点上
通常,依次选择坐标轴对空间切分.选择训练实例点在选定坐标轴上的中位数(median)为切分点,这样得到的kd树是平衡的.注意,平衡的kd树搜索时的效率未必是最优的
构造平衡kd树
输入:k维空间数据集
其中
输出:kd树
- 开始:构造根结点,根结点对应于包含的k维空间的超矩形区域
选择为坐标轴,以中所有实例的的中位数为切分点,将根结点对应的超矩形区域切分为两个子区域.切分由通过切分点并与坐标轴垂直的超平面
由根结点生成深度为1的左右子结点;左子结点对应坐标小于切分点的子区域,右子结点对应于坐标大于切分点的子区域
将落在切分超平面上的实例点保存在根结点
- 重复:对深度为j的结点,选择为切分的坐标轴,以该结点的区域中所有实例的坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域,切分由通过切分点并与坐标轴垂直的超平面实现
由该结点生成深度为j+1的左右子结点:左子结点对应坐标小于切分点的子区域,右子结点对应坐标大于切分点的子区域
将落在切分超平面上的实例点保存在该结点
- 直到两个子区域没有实例存在时停止,从而形成kd树的区域划分
实例2:给定一个二维空间的数据集
构造一个平衡kd树
解:根结点对应包含数据集的矩形,选择轴,6个数据点的坐标的中位数是7(注意:2,4,5,7,8,9在数学中的中位数为6,但因该算法的中值需在点集合之内,所以中值计算用的是len(points)/2=3,points[3]=(7,2)),以平面将空间分为左右两个子矩形(子结点);接着,左矩形以分为两个子矩形,右矩形以分为两个子矩形,如此递归,最后得到如图所示的特征空间划分和kd树
Image(filename="./data/3_5.png",width=500)

Image(filename="./data/3_4.png",width=500)

2.搜索kd树
利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量,这里以最近邻为例加以叙述,同样的方法可以应用到k近邻
给定一个目标点,搜索其最近邻.首先找到包含目标点的叶结点;然后从该叶结点出发,依次回退到父结点;不断查找与目标点最近邻的结点,当确定不可能存在更近的结点时终止,这样搜索就被限制在空间的局部区域上,效率大为提高
用kd树的最近邻搜索
输入:已构造的kd树,目标点x
输出:x的最近邻
-
在kd树中找出包含目标点x的叶结点;从根结点出发,递归地向下访问kd树,若目标点x当前维的坐标小于切分点的坐标,则移动左子结点,否则移动到右子结点,直到子结点为叶节点为止
-
以此叶节点为"当前最近点"
-
递归地向上回退,在每个节点进行一下操作
a.如果该结点保存的实例点比当前最近点距离目标点更近,则以该实例点为"当前最近点"
b.当前最近点一定存在于该结点一个子结点对应的区域.检查该子结点的父结点的另一个结点对应的区域是否有更近的点.具体地,检查另一子结点对应的区域是否与以目标点为球心,以目标点与"当前最近点"间的距离为半径的超球体相交
如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点.接着递归地进行最近邻搜索
如果不想交,向上回退 -
当回退到根结点时,搜索结束,最后的"当前最近点"即为x的最近邻点
如果实例点是随机分布的,kd树搜索的平均计算复杂度是
实例:给定一个如下图所示的kd树,根节点为A,其子结点为B,C等,树上共存储7个实例点;另一个输入目标实例点S,求S的最近邻
Image(filename="./data/3_8.png",width=500)

首先在kd树中找到包含点S的叶结点D(图中的右下区域),以点D作为近似最近邻.真正最近邻一定在以点S为中心通过点D的圆的内部.然后返回结点D的父结点B,在结点B的另一子结点F的区域内搜索最近邻,结点F的区域与圆不想交,不可能有最近邻点,继续返回上一级父结点A,在结点A的另一子结点C的区域内搜索最近邻,结点C的区域与圆相交;该区域在园内的实例点有点E,点E比点D更近,成为新的最近邻近似,最后得到点E是点S的最近邻
四.代码实现
1.度量距离
import math
from itertools import combinations
# p=1 Manhattan distance
# p=2 Euclidean distance
# p=3 Minkowski distance
def L(x,y,p=2):
# x1=[1,1] x2=[5,1]
if len(x)==len(y) and len(x)>1:
sum=0
for i in range(len(x)):
sum+=math.pow(abs(x[i]-y[i]),p)
return math.pow(sum,1/p)
else:
return 0
# 实例1
x1=[1,1]
x2=[5,1]
x3=[4,4]
# x1,x3
for i in range(1,5):
r={"1-{}".format(c):L(x1,c,p=i) for c in [x2,x3]}
print(min(zip(r.values(),r.keys())))
(4.0, '1-[5, 1]')
(4.0, '1-[5, 1]')
(3.7797631496846193, '1-[4, 4]')
(3.5676213450081633, '1-[4, 4]')
2.自定义KNN分析iris
遍历所有数据点,找出n个距离最近的点的分类情况,少数服从多数
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
iris=load_iris()
df=pd.DataFrame(iris.data,columns=iris.feature_names)
df["label"]=iris.target
df.columns=["sepal length","sepal width","petal length","petal width","label"]
# data=np.array(df.iloc[:100,[0,1,-1]])
df
| sepal length | sepal width | petal length | petal width | label | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | 0 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | 0 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | 0 |
| 5 | 5.4 | 3.9 | 1.7 | 0.4 | 0 |
| 6 | 4.6 | 3.4 | 1.4 | 0.3 | 0 |
| 7 | 5.0 | 3.4 | 1.5 | 0.2 | 0 |
| 8 | 4.4 | 2.9 | 1.4 | 0.2 | 0 |
| 9 | 4.9 | 3.1 | 1.5 | 0.1 | 0 |
| 10 | 5.4 | 3.7 | 1.5 | 0.2 | 0 |
| 11 | 4.8 | 3.4 | 1.6 | 0.2 | 0 |
| 12 | 4.8 | 3.0 | 1.4 | 0.1 | 0 |
| 13 | 4.3 | 3.0 | 1.1 | 0.1 | 0 |
| 14 | 5.8 | 4.0 | 1.2 | 0.2 | 0 |
| 15 | 5.7 | 4.4 | 1.5 | 0.4 | 0 |
| 16 | 5.4 | 3.9 | 1.3 | 0.4 | 0 |
| 17 | 5.1 | 3.5 | 1.4 | 0.3 | 0 |
| 18 | 5.7 | 3.8 | 1.7 | 0.3 | 0 |
| 19 | 5.1 | 3.8 | 1.5 | 0.3 | 0 |
| 20 | 5.4 | 3.4 | 1.7 | 0.2 | 0 |
| 21 | 5.1 | 3.7 | 1.5 | 0.4 | 0 |
| 22 | 4.6 | 3.6 | 1.0 | 0.2 | 0 |
| 23 | 5.1 | 3.3 | 1.7 | 0.5 | 0 |
| 24 | 4.8 | 3.4 | 1.9 | 0.2 | 0 |
| 25 | 5.0 | 3.0 | 1.6 | 0.2 | 0 |
| 26 | 5.0 | 3.4 | 1.6 | 0.4 | 0 |
| 27 | 5.2 | 3.5 | 1.5 | 0.2 | 0 |
| 28 | 5.2 | 3.4 | 1.4 | 0.2 | 0 |
| 29 | 4.7 | 3.2 | 1.6 | 0.2 | 0 |
| ... | ... | ... | ... | ... | ... |
| 120 | 6.9 | 3.2 | 5.7 | 2.3 | 2 |
| 121 | 5.6 | 2.8 | 4.9 | 2.0 | 2 |
| 122 | 7.7 | 2.8 | 6.7 | 2.0 | 2 |
| 123 | 6.3 | 2.7 | 4.9 | 1.8 | 2 |
| 124 | 6.7 | 3.3 | 5.7 | 2.1 | 2 |
| 125 | 7.2 | 3.2 | 6.0 | 1.8 | 2 |
| 126 | 6.2 | 2.8 | 4.8 | 1.8 | 2 |
| 127 | 6.1 | 3.0 | 4.9 | 1.8 | 2 |
| 128 | 6.4 | 2.8 | 5.6 | 2.1 | 2 |
| 129 | 7.2 | 3.0 | 5.8 | 1.6 | 2 |
| 130 | 7.4 | 2.8 | 6.1 | 1.9 | 2 |
| 131 | 7.9 | 3.8 | 6.4 | 2.0 | 2 |
| 132 | 6.4 | 2.8 | 5.6 | 2.2 | 2 |
| 133 | 6.3 | 2.8 | 5.1 | 1.5 | 2 |
| 134 | 6.1 | 2.6 | 5.6 | 1.4 | 2 |
| 135 | 7.7 | 3.0 | 6.1 | 2.3 | 2 |
| 136 | 6.3 | 3.4 | 5.6 | 2.4 | 2 |
| 137 | 6.4 | 3.1 | 5.5 | 1.8 | 2 |
| 138 | 6.0 | 3.0 | 4.8 | 1.8 | 2 |
| 139 | 6.9 | 3.1 | 5.4 | 2.1 | 2 |
| 140 | 6.7 | 3.1 | 5.6 | 2.4 | 2 |
| 141 | 6.9 | 3.1 | 5.1 | 2.3 | 2 |
| 142 | 5.8 | 2.7 | 5.1 | 1.9 | 2 |
| 143 | 6.8 | 3.2 | 5.9 | 2.3 | 2 |
| 144 | 6.7 | 3.3 | 5.7 | 2.5 | 2 |
| 145 | 6.7 | 3.0 | 5.2 | 2.3 | 2 |
| 146 | 6.3 | 2.5 | 5.0 | 1.9 | 2 |
| 147 | 6.5 | 3.0 | 5.2 | 2.0 | 2 |
| 148 | 6.2 | 3.4 | 5.4 | 2.3 | 2 |
| 149 | 5.9 | 3.0 | 5.1 | 1.8 | 2 |
150 rows × 5 columns
plt.scatter(df[:50]["sepal length"],df[:50]["sepal width"],label="0")
plt.scatter(df[50:100]["sepal length"],df[50:100]["sepal width"],label="1")
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.legend()
<matplotlib.legend.Legend at 0x18193faffd0>

data=np.array(df.iloc[:100,[0,1,-1]])
X,y=data[:,:-1],data[:,-1]
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
class KNN(object):
def __init__(self,X_train,y_train,n_neighbors=3,p=2):
"""
parameter:n_neighbors 临近点个数
parameter:p 距离度量
"""
self.n=n_neighbors
self.p=p
self.X_train=X_train
self.y_train=y_train
def predict(self,X):
# 取出n个点
knn_list=[]
for i in range(self.n):
dist=np.linalg.norm(X-self.X_train[i],ord=self.p)
knn_list.append((dist,self.y_train[i]))
for i in range(self.n,len(self.X_train)):
max_index=knn_list.index(max(knn_list,key=lambda x:x[0]))
dist=np.linalg.norm(X-self.X_train[i],ord=self.p)
if knn_list[max_index][0]>dist:
knn_list[max_index]=(dist,self.y_train[i])
# 统计
knn=[k[-1] for k in knn_list]
count_pairs=Counter(knn)
max_count=sorted(count_pairs,key=lambda x:x)[-1]
return max_count
def score(self,X_test,y_test):
right_count=0
n=10
for X,y in zip(X_test,y_test):
label=self.predict(X)
if label==y:
right_count+=1
return right_count/len(X_test)
clf=KNN(X_train,y_train)
clf.score(X_test,y_test)
1.0
test_point=[6.0,3.0]
print("Test Point:{}".format(clf.predict(test_point)))
Test Point:1.0
plt.scatter(df[:50]["sepal length"],df[:50]["sepal width"],label="0")
plt.scatter(df[50:100]["sepal length"],df[50:100]["sepal width"],label="1")
plt.plot(test_point[0],test_point[1],"bo",label="test_point")
plt.xlabel("sepal length")
plt.ylabel("sepal width")
plt.legend()
<matplotlib.legend.Legend at 0x181944c5588>

3.sklearn实现KNN
from sklearn.neighbors import KNeighborsClassifier
clf_sk=KNeighborsClassifier()
clf_sk.fit(X_train,y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=5, p=2,
weights='uniform')
clf_sk.score(X_test,y_test)
1.0
sklearn.neighbors.KNeighborsClassifier主要参数说明:
- n_neighbors:临近点个数
- p:度量距离
- algorithm:近邻算法,可选{“auto”,“ball_tree”,“kd_tree”,“brute”}
- weights:确定近邻的权重
4.kd树
# kd-tree每个结点中主要包含的数据结构如下
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k维向量节点(k维空间中的一个样本点)
self.split = split # 整数(进行分割维度的序号)
self.left = left # 该结点分割超平面左子空间构成的kd-tree
self.right = right # 该结点分割超平面右子空间构成的kd-tree
class KdTree(object):
def __init__(self, data):
k = len(data[0]) # 数据维度
def CreateNode(split, data_set): # 按第split维划分数据集exset创建KdNode
if not data_set: # 数据集为空
return None
# key参数的值为一个函数,此函数只有一个参数且返回一个值用来进行比较
# operator模块提供的itemgetter函数用于获取对象的哪些维的数据,参数为需要获取的数据在对象中的序号
#data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序
data_set.sort(key=lambda x: x[split])
split_pos = len(data_set) // 2 # //为Python中的整数除法
median = data_set[split_pos] # 中位数分割点
split_next = (split + 1) % k # cycle coordinates
# 递归的创建kd树
return KdNode(median, split,
CreateNode(split_next, data_set[:split_pos]), # 创建左子树
CreateNode(split_next, data_set[split_pos + 1:])) # 创建右子树
self.root = CreateNode(0, data) # 从第0维分量开始构建kd树,返回根节点
# KDTree的前序遍历
def preorder(root):
print (root.dom_elt)
if root.left: # 节点不为空
preorder(root.left)
if root.right:
preorder(root.right)
# 对构建好的kd树进行搜索,寻找与目标点最近的样本点:
from math import sqrt
from collections import namedtuple
# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 数据维度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正负无穷
nodes_visited = 1
s = kd_node.split # 进行分割的维度
pivot = kd_node.dom_elt # 进行分割的“轴”
if target[s] <= pivot[s]: # 如果目标点第s维小于分割轴的对应值(目标离左子树更近)
nearer_node = kd_node.left # 下一个访问节点为左子树根节点
further_node = kd_node.right # 同时记录下右子树
else: # 目标离右子树更近
nearer_node = kd_node.right # 下一个访问节点为右子树根节点
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 进行遍历找到包含目标点的区域
nearest = temp1.nearest_point # 以此叶结点作为“当前最近点”
dist = temp1.nearest_dist # 更新最近距离
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近点将在以目标点为球心,max_dist为半径的超球体内
temp_dist = abs(pivot[s] - target[s]) # 第s维上目标点与分割超平面的距离
if max_dist < temp_dist: # 判断超球体是否与超平面相交
return result(nearest, dist, nodes_visited) # 不相交则可以直接返回,不用继续判断
#----------------------------------------------------------------------
# 计算目标点与分割点的欧氏距离
temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近点
dist = temp_dist # 更新最近距离
max_dist = dist # 更新超球体半径
# 检查另一个子结点对应的区域是否有更近的点
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一个子结点内存在更近距离
nearest = temp2.nearest_point # 更新最近点
dist = temp2.nearest_dist # 更新最近距离
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 从根节点开始递归
# 实例2
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)
[7, 2]
[5, 4]
[2, 3]
[4, 7]
[9, 6]
[8, 1]
from time import clock
from random import random
# 产生一个k维随机向量,每维分量值在0~1之间
def random_point(k):
return [random() for _ in range(k)]
# 产生n个k维随机向量
def random_points(k, n):
return [random_point(k) for _ in range(n)]
ret = find_nearest(kd, [3,4.5])
print (ret)
Result_tuple(nearest_point=[2, 3], nearest_dist=1.8027756377319946, nodes_visited=4)
N = 400000
t0 = clock()
kd2 = KdTree(random_points(3, N)) # 构建包含四十万个3维空间样本点的kd树
ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四十万个样本点中寻找离目标最近的点
t1 = clock()
print ("time: ",t1-t0, "s")
print (ret2)
E:Anacondaenvsmytensorflowlibsite-packagesipykernel_launcher.py:2: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
time: 6.159827752999263 s
Result_tuple(nearest_point=[0.09732020950704356, 0.49930092577904095, 0.8029864162744909], nearest_dist=0.004072918366121865, nodes_visited=42)
E:Anacondaenvsmytensorflowlibsite-packagesipykernel_launcher.py:5: DeprecationWarning: time.clock has been deprecated in Python 3.3 and will be removed from Python 3.8: use time.perf_counter or time.process_time instead
"""