KMP算法

模板题：

给出两个字符串A和B，其中A为B的子串，求出A在B中所有出现的次数。

首先，字符串匹配的朴素算法就是枚举B串的每一个元素，然后当 $B[i]$ 和 $A[1]$ 相等时，在枚举 $B[i+1]$ 和 $A[2]$...依次类推，直到A和B的子串完全匹配是输出A所在的位置就OK啦

But，它的时间复杂度是 $O(nm)$（n，m是字符串A,B的长度）

当n，m超过一定程度是就要T了

所以KMP出现了

KMP算法是一种可以在线性时间内，判断字符串A是否为字符串B的子串，并求出A在B出现的位置的神奇算法（反正很高级就好了）

不过字符串Hash也可以在 $O(n)$ 的时间内预处理，并且支持 $O(1)$ 查询，不过好像莫得KMP方便

下面是KMP与暴力的区别

在 $B[i]$ 和 $A[j]$ 匹配失败后，i只向后移动了一个，这就浪费了很多时间，所以KMP出现了

我们可以预处理出一个next数组，记录匹配失败后下一次的匹配的 $i$（如何处理等会讲），然后就可以跳过中间的无用的匹配，就可以节约很多时间

这就好比打游戏的时候，你在Boss关输了，本来要重新开始的，但是你在中途存档了，就可以直接跳关，节约时间

（算阶还有一个 $f[i]$ 表示B中以 $i$ 结尾的子串与A的前缀能够匹配的最长长度，这个锅最后补（手动尴尬））

下面进入next数组的计算方法

首先 $next[i]$ 表示A中以 $i$ 结尾的非前缀子串与A的前缀能匹配的最长长度

很显然对吧，如果你能看懂的话，那真是太好了，因为你可以跳过下面的理解教程

手动理解中

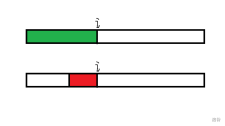
红色的是以i结尾的非前缀子串，绿色的是A的前缀

所以next数组就是红色为绿色的真子集（绿色包含红色，但绿色不等于红色）时，红色的最长长度

（画个图就好理解多了）

=理解完毕=

怎么用代码实现呢。。。

某蒟蒻lcg（举手）:枚举 $j$ 和 $i$ 的大小，并查找 $A[1\sim j]$ 和 $A[i-j+1\sim i]$ 是否相等

很好，某个菜鸡已经讲出了$O(n^2)$的预处理，我们得到了一个比暴力还慢的预处理了

如何在更短的时间里求出next数组呢？

我们首先要证明当 $next[i]$ 可以为 $j$ 时，小于 $j$ 能选择的最大值为 $next[j]$

~~证明：易证，证毕~~

证明：（不会反证法的左转）

假设有 $next[j_0]<j_1<j_0，使 $next[i]$ 可以选择 $j_1$

如图所示：

明显可以看出 $next[j_0]$ 是包含在 $next[j_1]$ 里的

又因为next数组表示在当前位置能匹配到的最大值，而 $j_1$ 比 $next[j_0]$ 更优，这与next的定义矛盾，所以假设不正确

因此

当$next[i]$可以为$j$时，小于$j$能选择的最大值为$next[j]$

然后就可以进行预处理，在求$next[i]$时，我们只需要在$next[i-1]+1,next[next[i-1]]+1...$找符合要求的值就OK了

代码实现:

初始化$next[1]=0$,不断尝试匹配$j$，如果失败，使$j=next[j]$，直到$j==0$；如果匹配成功则$j++$

next[1]=0;
for(int i=2,j=0;i<=n;i++){
	while(j>0&&b[i]!=b[j+1]) j=next[j];
	if(b[i]==b[j+1]) j++;
	next[i]=j;
}

下面是字符串的比较了（顺带说一下f数组）

for(int i=1,j=0;i<=m;i++){
	while(j>0&&(j==n||b[i]!=a[j+1])) j=next[j];
	f[i]=j;//直接赋值即可
	if(j==n) ans++;//匹配成功
}

最后输出ans即可