调频连续波原理
FMCW(Frequency Modulated Continuous Wave),即调频的连续信号。在许多方面得到应用,比如生物雷达,车载雷达,无人机雷达等等方面都有FMCW波的应用,目前的商业化的雷达模块大多使用的该原理来实现雷达的测距,测速。
1 信号的模型
一般而言我们使用Chirp信号。下图为一个典型的Chirp信号的模型,从时域波看,其波形时一个频率随时间线性变换的波形。设线性调制波的波形的是锯齿波。则下图为典型的Chirp信号在时域和频域的图形如图所示。所以可以发射信号的公式(1):
\[S_t(t) = Acos[2\pi(f_0+S*t)t+\phi_0]\tag1
\]
其中\(S\)为锯齿波的斜率,值为信号的调频的带宽除于调制的周期\(\frac{B}{T_c}\),所以式子(1)的相位可以写为以下的形式(2):
\[p_(t) = {2\pi[(f_0+\frac{B}{2})t+\frac{1}{2T}Bt^2]+\phi_0},t\in[0,T_c]\tag2
\]
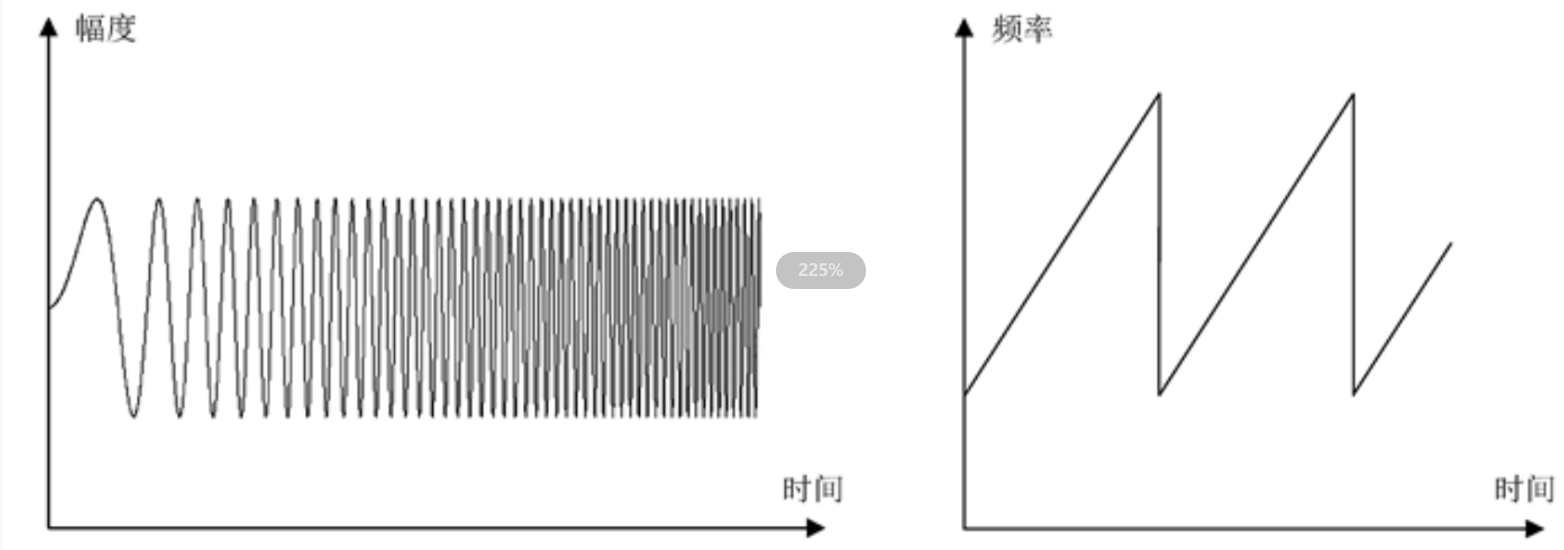
图1 chirp信号的时域图和f-t图
补充以下简单的数学知识,相位的导数是频率,下边的公式(3)
\[f = \frac{\partial\phi(t)}{2\pi\partial t}\tag3
\]
2 静止情况测距
设静止的目标距离雷达的距离为\(R\),电磁波在空气中传输速度为c,则接受的信号接受机接受到的信号比发射的信号延迟\(\tau = \frac{2R}{c}\),所以理想中接受机的目标回波信号如为式(4):
\[S_r(t) = KAcos(2\pi[(f_0+\frac{B}{2})(t-\tau)+\frac{1}{2T}B(t-\tau)^2]+\phi_0)\tag4
\]
将接收到信号\(S_r(t)和S_t(t)\)进行混频处理,处理的简单图如图所示。对于当个目标得到的频率图如图2所示,

图2 回波信号和发射信号
图中黑色的虚线便是中频信号的频率,这个时候很明显的看出发射信号和单目标的回波信号的频率差为一个单频信号由公式(4)得到接收回波信号的相位表达式子(5):
$$
p_r=2\pi[(f_0+\frac{B}{2})(t-\tau)+\frac{1}{2T}B(t-\tau)^2]+\phi_0\tag5
$$
则中频信号的相位公式(6)为:
$$
\begin{align}
p_m(t) &= p_s(t) - p_r(t)\
&=2\pi \frac{B}{T_c} \frac{2R}{c}t \tag6
\end{align}
通过这个式子可以知道中频的频率为\(f_{IF} = 2\pi \frac{B}{T_c} \frac{2R}{c}\),所以在雷达系统中可以将中频使用ADC变成数字信号后使用FFT测量频率\(f_{IF}\),其他的参数可知来测量\(R\),显然距离公式R为(7):
\[R=\frac{_{f_{IF}T_c c}}{2\pi B}\tag 7
\]
同理该原理可以推到多目标的情况,当目标多于单个时候,计算得到的FFT的频率谱存在多个峰值,如图3所示
图3 多目标频域示意图
### 3 运动情况下测速
设在电磁波的覆盖区域中,某一目标在\(t_0\)时刻距离发射天线为\(R_0\),以径向\(v\)远离天线(以远离天线为正方向),那么接受到的目标的回波信号公式如(4)所示,但是\(\tau\)有所改变,\(\tau = \frac{2R(t)}{c} = \frac{2(R_0+vt)}{c}\)为信号的延时,这个时候通过混频后得到中频信号的相位如(8):
\[\begin{align}\notag
p_m(t) &= p_s(t) - p_r(t)\\
&=2\pi \{{[\frac{2}{c}(f_0+\frac{B}{2})v-\frac{4BR_0v}{Tc^2}+\frac{2BR_0}{Tc}]t
+(\frac{2Bv}{Tc}-\frac{2Bv^2}{Tc^2})t^2+\frac{2R_0}{c}(f_0+\frac{B}{2})-\frac{2BR_0}{Tc^2}}\}\tag8
\end{align}
\]
很显然对于运动的信号的中频信号依然是一个线性调频信号,所以信号的参数带宽\(B_m\),载频\(f_m\),初相\(\phi_m\)
\[\begin{align}\notag
B_m &= \frac{4Bv}{c}-\frac{4Bv^2}{c^2}\tag9 \\
f_m& = \frac{2BR_0}{Tc}+\frac{2vf_0}{c}+\frac{Bv}{c}-\frac{4BR_0v}{Tc^2}+\frac{2Bv^2}{c^2}\notag \\
&\approx\frac{2BR_0}{Tc}+\frac{2vf_0}{c}\tag{10}\\
\phi_m &=2\pi[\frac{2R_0}{c}(f_0+\frac{B}{2})-\frac{2BR_0}{Tc^2}]\tag{11}
\end{align}
\]
所以运动下的回波信号的中频信号依然可以写成(12):
\[r_m(t) = A_mcos\{{2\pi[(f_m+\frac{B_m}{2})t+\frac{1}{2T}B_mt^2]+\phi_m}\} \tag{12}
\]
写成复指数的形式(13):
\[r_m(t) = A_m e^{j\phi_m}.e^{[{j2\pi(f_m+\frac{B_m}{2})t+\frac{\pi}{T}B_mt^2}]} \tag{13}
\]
这个时候可以得到运动信号的中频信号,从(9)~(11)式子中可以显然看出带宽\(B_m\),载频\(f_m\),初相\(\phi_m\)都和目标的\(v\)存在联系。现在对其采样从模拟信号转化到数字信号来进入数字芯片进行处理,得到距离和速度的信息。设我们使用的ADC的采样时间为\(T_s\),得到离散化后的信号\(r[n]\)。并对其使用DFT计算(15):
\[\begin{align}
r_m[n] &= A_m e^{j\phi_m}.e^{\{j2\pi[(f_m+\frac{B_m}{2})nT_s+\frac{\pi}{T}B_m(nT_s)^2]\}} \tag{14} \\
X[k]&= DFT(r[n]) = \sum_{n=0}^{N-1} r[k] e^{\frac{-j2\pi kn}{N}} \notag \\
&=A_m e^{j\phi_m}.\sum_{n=0}^{N-1}e^{\{j2\pi[(f_m+\frac{B_m}{2})nT_s+\frac{1}{2T}B_m(n^T_s)^2]-\frac{kn}{N}\}}\tag{15}
\end{align}
\]
\(f_m\)和速度\(v\)和\(R_0\)有关,但是在扫频过程中,\(f_m\)的变化不大,所以不容易计算出目标的径向速度,但是可以得到在扫频周期,信号的包络\(\chi_l[k]\)。
\[\begin{align}
\chi_l[k]&=A_m e^{j\phi_m} \notag \\
&=A_me^{\{j2\pi[\frac{2R_0+VTl)}{c}(f_0+\frac{B}{2}) -\frac{2B(R_0+vlT)^2}{Tc^2}]\}} \ \ l=0,1,2...M \tag{16}
\end{align}
\]
通过数学计算,有兴趣自己计算
\[\begin{align}
f_v &= \frac{(f_0+\frac{B}{2})v}{c}-\frac{4BR_0v}{Tc^2}\notag\\
&\approx\frac{(f_0+\frac{B}{2})v}{c} \tag{17}
\end{align}
\]
这样就可以得到速度和距离的信息,这个是基本的调频连续波测速和测距的原理。


