题目链接:https://www.acwing.com/activity/content/punch_the_clock/6/
最短路有很多种解法:
BFS
只适用于边权为1的图。
DP
只适用于DAG的解法,当一个点不存在入边,那么他的答案是可以立刻确定的。这个算法除了DAG以外没有任何要求,可以跑带负权的图。
Dijkstra
高效、稳定的单源最短路算法,适用于处理非负权边的情况。
复杂度为: (O((n+m)log(n+m)))
int n;
vector<pii> G[MAXN + 5];
bool vis[MAXN + 5];
int dis[MAXN + 5];
priority_queue<pii> PQ;
void Dijkstra(int s) {
while(!PQ.empty())
PQ.pop();
memset(vis, 0, sizeof(vis[0]) * (n + 1));
memset(dis, INF, sizeof(dis[0]) * (n + 1));
dis[s] = 0;
PQ.push({-dis[s], s});
while(!PQ.empty()) {
int u = PQ.top().second;
PQ.pop();
if(vis[u])
continue;
vis[u] = 1;
for(auto &e : G[u]) {
int v = e.first, w = e.second;
if(dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
PQ.push({-dis[v], v});
}
}
}
return;
}
常见的技巧有:
反向建图:源点为整个点击,汇点却只有单个,这时可能把边反向。
分层建图:指定某些边可以使用一些特殊性质,比如可以使用一些魔法降低边的权值,但是魔法力量有限。这种问题一般魔法力量的范围不会太大,刚刚好可以把原图的每个点都拆成魔法力量的范围这么多,注意提取边的公共性质来减少边的存储。
多个点同时作为源点:区别于多源最短路,这里求源点集到每个点的最短路,可以建一个超级源点,然后向源点集连权值为0的边,或者直接把整个点集都全部丢到 PQ 里面。
单源单汇:类似双向BFS,退出的时候会快一点。或者在汇点被push从PQ中pop出去的同时退出也可以加速。
双端BFS
又称0-1BFS,使用双端队列代替队列的BFS,适用于边权值只有0和1的图,也可以理解为手动控制优先队列的Dijkstra算法(事实上这几个都没什么区别)。
复杂度为: (O(n+m))
vector<pii> G[MAXN + 5];
int dis[MAXN + 5];
deque<int> DQ;
void BFS(int s, int Limit) {
DQ.clear();
memset(dis, INF, sizeof(dis[0]) * (n + 1));
dis[s] = 0;
DQ.push_back(s);
while(!DQ.empty()) {
int u = DQ.front();
DQ.pop_front();
if(u == n)
break;
for(auto &e : G[u]) {
int v = e.first, w = e.second;
if(w == 0) {
if(dis[u] < dis[v]) {
dis[v] = dis[u];
DQ.push_front(v);
}
} else {
if(dis[u] + 1 < dis[v]) {
dis[v] = dis[u] + 1;
DQ.push_back(v);
}
}
}
}
return;
}
技巧:
有可能可以把一些问题转换成0-1BFS来解决,例如下面的340,是求最大值+分层建图,因为可以二分最大值,然后根据与最大值的关系来区分边权是0还是1,分层建图的同时就是进行BFS的过程。
SPFA
又称“队列优化的Bellman-Ford算法”,复杂度是很假的,最坏可以退化到 (O(nm)) 。适用于任何图,若不存在从源点出发能到达的负环,则SPFA可以计算出单源最短路,否则会在同一个节点入队超过n次之后报告存在负环。
Floyd
实现非常简单的,任意两点间的最短路,也可以正确检测出负环。(Floyd结束后存在自己到自己的最短路为负数的点,那么可以无限绕圈圈)缺点是复杂度过大。只适用于很小的图。
340. 通信线路
题意:在郊区有 N 座通信基站,P 条 双向电缆,第 i 条电缆连接基站 Ai 和 Bi。特别地,1 号基站是通信公司的总站,N 号基站位于一座农场中。现在,农场主希望对通信线路进行升级,其中升级第 i 条电缆需要花费 Li 。电话公司正在举行优惠活动。农场主可以指定一条从 1 号基站到 N 号基站的路径,并指定路径上不超过 K 条电缆,由电话公司免费提供升级服务。农场主只需要支付在该路径上剩余的电缆中,升级价格最贵的那条电缆的花费即可。求至少用多少钱可以完成升级。
数据范围:
0≤K<N≤1000,
1≤P≤10000,
1≤Li≤1000000
题解:
分层图Dijkstra
从特殊到一般,先考虑 K=0 的情形,这个时候是要找一条最短路,只不过不是加法运算而是 max 运算,用 Dijkstra 算法可以直接求解。注意到好像以前做过这类题目(貌似第一次见是2018年多校)都从分层图去考虑。观察一下数据范围,确实可以建分层图。
把一个点拆成 K+1 个点,二元组 (id,k) 表示编号为 id 的点已经使用了 k 次免费的状态,那么原本的边也拆成超级多条边,不过非常容易注意到这些边可以高度压缩。
复杂度为 (O(n*k*log(n*k))) 。
vector写法:
const int MAXNK = 1000 * 1001;
int n, p, k;
vector<pii> G[MAXNK + 5];
int id_ki_pos(int id, int ki) {
return (id - 1) * (k + 1) + ki + 1;
}
int pos_id(int pos) {
return (pos - 1) / (k + 1) + 1;
}
int pos_ki(int pos) {
return (pos - 1) % (k + 1);
}
bool vis[MAXNK + 5];
int dis[MAXNK + 5];
priority_queue<pii> PQ;
void Dijkstra(int sid) {
while(!PQ.empty())
PQ.pop();
memset(vis, 0, sizeof(vis[0]) * (n + 1) * (k + 1));
memset(dis, INF, sizeof(dis[0]) * (n + 1) * (k + 1));
int spos = id_ki_pos(sid, 0);
dis[spos] = 0;
PQ.push({-dis[spos], spos});
while(!PQ.empty()) {
int upos = PQ.top().second;
PQ.pop();
if(vis[upos])
continue;
vis[upos] = 1;
int uid = pos_id(upos);
int uki = pos_ki(upos);
if(uid == n)
break;
for(auto &e : G[uid]) {
int vid = e.first, w = e.second;
{
int v0pos = id_ki_pos(vid, uki);
if(max(dis[upos], w) < dis[v0pos]) {
dis[v0pos] = max(dis[upos], w);
PQ.push({-dis[v0pos], v0pos});
}
}
if(uki < k) {
int v1pos = id_ki_pos(vid, uki + 1);
if(max(dis[upos], 0) < dis[v1pos]) {
dis[v1pos] = max(dis[upos], 0);
PQ.push({-dis[v1pos], v1pos});
}
}
}
}
return;
}
void TestCase() {
scanf("%d%d%d", &n, &p, &k);
for(int i = 1; i <= n; ++i)
G[i].clear();
for(int i = 1; i <= p; ++i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
G[u].push_back({v, w});
G[v].push_back({u, w});
}
Dijkstra(1);
int ans = INF;
for(int ki = 0; ki <= k; ++ki)
ans = min(ans, dis[id_ki_pos(n, ki)]);
if(ans == INF)
ans = -1;
printf("%d
", ans);
return;
}
链式前向星写法:
const int MAXNK = 1000 * 1001;
const int MAXP = 1000000;
int n, p, k;
int G[MAXNK + 5];
struct Edge {
int v, w, nxt;
Edge() {}
Edge(int v, int w, int nxt): v(v), w(w), nxt(nxt) {}
} edge[MAXP * 2 + 5];
int top;
void Init() {
top = 0;
memset(G, -1, sizeof(G[0]) * (n + 1));
}
void AddEdge(int u, int v, int w) {
++top;
edge[top] = Edge(v, w, G[u]);
G[u] = top;
}
int id_ki_pos(int id, int ki) {
return (id - 1) * (k + 1) + ki + 1;
}
int pos_id(int pos) {
return (pos - 1) / (k + 1) + 1;
}
int pos_ki(int pos) {
return (pos - 1) % (k + 1);
}
bool vis[MAXNK + 5];
int dis[MAXNK + 5];
priority_queue<pii> PQ;
void Dijkstra(int sid) {
while(!PQ.empty())
PQ.pop();
memset(vis, 0, sizeof(vis[0]) * (n + 1) * (k + 1));
memset(dis, INF, sizeof(dis[0]) * (n + 1) * (k + 1));
int spos = id_ki_pos(sid, 0);
dis[spos] = 0;
PQ.push({-dis[spos], spos});
while(!PQ.empty()) {
int upos = PQ.top().second;
PQ.pop();
if(vis[upos])
continue;
vis[upos] = 1;
int uid = pos_id(upos);
int uki = pos_ki(upos);
if(uid == n)
break;
for(int eid = G[uid]; eid != -1; eid = edge[eid].nxt) {
int vid = edge[eid].v, w = edge[eid].w;
{
int v0pos = id_ki_pos(vid, uki);
if(max(dis[upos], w) < dis[v0pos]) {
dis[v0pos] = max(dis[upos], w);
PQ.push({-dis[v0pos], v0pos});
}
}
if(uki < k) {
int v1pos = id_ki_pos(vid, uki + 1);
if(max(dis[upos], 0) < dis[v1pos]) {
dis[v1pos] = max(dis[upos], 0);
PQ.push({-dis[v1pos], v1pos});
}
}
}
}
return;
}
void TestCase() {
scanf("%d%d%d", &n, &p, &k);
Init();
for(int i = 1; i <= p; ++i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
AddEdge(u, v, w);
AddEdge(v, u, w);
}
Dijkstra(1);
int ans = INF;
for(int ki = 0; ki <= k; ++ki)
ans = min(ans, dis[id_ki_pos(n, ki)]);
if(ans == INF)
ans = -1;
printf("%d
", ans);
return;
}
收获:
- 这些下标比较烦人,要先在纸上画清楚。
- 边数比较大,层数也比较大,全部加边容易卡空间,我看见那个全部加边的写法简直是扯淡。
- 链式前向星的速度比vector显著快,大概快6倍,极有可能是没有打开O2优化。
二分+双端BFS
题目要求的是最小化最大值,是一种常见的二分+验证的题目,假如二分枚举一个最大值maxw,只需要把所有<=maxw的边记作cost=0(不使用免费次数),而把>maxw的边记作cost=1(使用1次免费次数),变成经典的0-1BFS问题,用双端队列解决,cost=1的从队尾加入,cost=0的从队首加入。
实际证明这个算法是最快的,也非常省空间,因为双端BFS常数极小,且验证速度极快(验证速度 (O(n)) )。
复杂度为 (O(n*log MAXL)) 。
const int MAXN = 1000;
const int MAXP = 1000000;
int n, p, k;
int G[MAXN + 5];
struct Edge {
int v, w, nxt;
Edge() {}
Edge(int v, int w, int nxt): v(v), w(w), nxt(nxt) {}
} edge[MAXP * 2 + 5];
int top;
void Init() {
top = 0;
memset(G, -1, sizeof(G[0]) * (n + 1));
}
void AddEdge(int u, int v, int w) {
++top;
edge[top] = Edge(v, w, G[u]);
G[u] = top;
}
int dis[MAXN + 5];
deque<int> DQ;
bool BFS(int s, int Limit) {
DQ.clear();
memset(dis, INF, sizeof(dis[0]) * (n + 1));
dis[s] = 0;
DQ.push_back(s);
while(!DQ.empty()) {
int u = DQ.front();
DQ.pop_front();
if(u == n)
break;
for(int eid = G[u]; eid != -1; eid = edge[eid].nxt) {
int v = edge[eid].v, w = edge[eid].w;
if(w <= Limit) {
if(dis[u] < dis[v]) {
dis[v] = dis[u];
DQ.push_front(v);
}
} else {
if(dis[u] + 1 < dis[v]) {
dis[v] = dis[u] + 1;
DQ.push_back(v);
}
}
}
}
return dis[n] <= k;
}
void TestCase() {
scanf("%d%d%d", &n, &p, &k);
Init();
for(int i = 1; i <= p; ++i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
AddEdge(u, v, w);
AddEdge(v, u, w);
}
int L = 0, R = INF, ans;
while(1) {
int M = (L + R) >> 1;
if(L == M) {
if(BFS(1, L)) {
ans = L;
break;
}
ans = R;
break;
}
if(BFS(1, M))
R = M;
else
L = M + 1;
}
if(ans == INF)
ans = -1;
printf("%d
", ans);
return;
}
收获:
- 最小化最大值的问题,可以尝试转化成二分枚举+快速验证。
- 不要搞错二分的值域,这里从0开始。
- 二分时初始R为无穷大,二分达到无穷大说明无解。
- BFS不需要vis数组。
341. 最优贸易
题意:C国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为1条。C国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。商人阿龙来到C国旅游。当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚一点旅费。设C国 n 个城市的标号从 1~n,阿龙决定从1号城市出发,并最终在 n 号城市结束自己的旅行。在旅游的过程中,任何城市可以被重复经过多次,但不要求经过所有 n 个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。因为阿龙主要是来C国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。
请你告诉阿龙,他最多能赚取多少旅费。
数据范围:
1≤n≤100000,
1≤m≤500000,
1≤各城市水晶球价格≤100
题解:因为各个城市可以反复经过,所以问题变成了这样:从1号城市出发,到达x号城市,购买一个水晶球;从x号城市出发,到达y号城市,卖出一个水晶球;从y号城市出发,到达n号城市。看一下数据,水晶球的价格貌似是突破口?
假算法:这道题有个非常明显的强连通分量的解法,首先把所有的强连通分量缩点,记录每个新点的最大值、最小值,然后变成一个DAG。再从新图中包含原图的1号点为源点找出到其他点的路径上的最小值(Dijkstra),然后从新图中包含原图的n号点为汇点找出其他点到汇点的路径上的最大值(反向图上Dijkstra),然后对遍历一遍差取最大值。
const int MAXN = 1e5;
int n, m;
int price[MAXN + 5];
namespace SCC {
int n;
vector<int> G[MAXN + 5], BG[MAXN + 5];
int c1[MAXN + 5], cntc1;
int c2[MAXN + 5], cntc2;
int s[MAXN + 5], cnts;
int n2;
vector<int> V2[MAXN + 5];
vector<int> G2[MAXN + 5], BG2[MAXN + 5];
void Init(int _n) {
n = _n;
cntc1 = 0, cntc2 = 0, cnts = 0;
for(int i = 1; i <= n; ++i) {
G[i].clear();
BG[i].clear();
c1[i] = 0;
c2[i] = 0;
s[i] = 0;
V2[i].clear();
G2[i].clear();
BG2[i].clear();
}
return;
}
void AddEdge(int u, int v) {
G[u].push_back(v);
BG[v].push_back(u);
return;
}
void dfs1(int u) {
c1[u] = cntc1;
for(auto &v : G[u]) {
if(!c1[v])
dfs1(v);
}
s[++cnts] = u;
}
void dfs2(int u) {
V2[cntc2].push_back(u);
c2[u] = cntc2;
for(auto &v : BG[u]) {
if(!c2[v])
dfs2(v);
}
return;
}
void Kosaraju() {
for(int i = 1; i <= n; ++i) {
if(!c1[i]) {
++cntc1;
dfs1(i);
}
}
for(int i = n; i >= 1; --i) {
if(!c2[s[i]]) {
++cntc2;
dfs2(s[i]);
}
}
return;
}
void Build() {
n2 = cntc2;
for(int i = 1; i <= n2; ++i) {
for(auto &u : V2[i]) {
for(auto &v : G[u]) {
if(c2[v] != i) {
G2[i].push_back(c2[v]);
BG2[c2[v]].push_back(i);
}
}
}
}
for(int i = 1; i <= n2; ++i) {
sort(G2[i].begin(), G2[i].end());
G2[i].erase(unique(G2[i].begin(), G2[i].end()), G2[i].end());
sort(BG2[i].begin(), BG2[i].end());
BG2[i].erase(unique(BG2[i].begin(), BG2[i].end()), BG2[i].end());
}
return;
}
int minV2[MAXN + 5], maxV2[MAXN + 5];
bool vis[MAXN + 5];
priority_queue<pii> PQ;
int mindis[MAXN + 5];
void DijkstraMin(int s) {
while(!PQ.empty())
PQ.pop();
memset(vis, 0, sizeof(vis[0]) * (n2 + 1));
memset(mindis, INF, sizeof(mindis[0]) * (n2 + 1));
mindis[s] = minV2[s];
PQ.push({-mindis[s], s});
while(!PQ.empty()) {
int u = PQ.top().second;
PQ.pop();
if(vis[u])
continue;
vis[u] = 1;
for(auto &v : G2[u]) {
if(mindis[u] < mindis[v]) {
mindis[v] = min(minV2[v], mindis[u]);
PQ.push({-mindis[v], v});
}
}
}
return;
}
int maxdis[MAXN + 5];
void DijkstraMax(int s) {
while(!PQ.empty())
PQ.pop();
memset(vis, 0, sizeof(vis[0]) * (n2 + 1));
memset(maxdis, -INF, sizeof(maxdis[0]) * (n2 + 1));
maxdis[s] = maxV2[s];
PQ.push({maxdis[s], s});
while(!PQ.empty()) {
int u = PQ.top().second;
PQ.pop();
if(vis[u])
continue;
vis[u] = 1;
for(auto &v : BG2[u]) {
if(maxdis[u] > maxdis[v]) {
maxdis[v] = max(maxV2[v], maxdis[u]);
PQ.push({maxdis[v], v});
}
}
}
return;
}
void Solve() {
for(int i = 1; i <= n2; ++i) {
minV2[i] = INF, maxV2[i] = -INF;
for(auto &u : V2[i]) {
minV2[i] = min(minV2[i], price[u]);
maxV2[i] = max(maxV2[i], price[u]);
}
}
DijkstraMin(c2[1]);
DijkstraMax(c2[n]);
int ans = 0;
for(int i = 1; i <= n2; ++i)
ans = max(ans, maxdis[i] - mindis[i]);
printf("%d
", ans);
return;
}
}
void TestCase() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i)
scanf("%d", &price[i]);
SCC::Init(n);
for(int i = 1; i <= m; ++i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
SCC::AddEdge(u, v);
if(w == 2)
SCC::AddEdge(v, u);
}
SCC::Kosaraju();
SCC::Build();
SCC::Solve();
return;
}
注意点权Dijkstra也是要先初始化为无穷(而不是对应的点权),然后在vis节点(可以在入PQ的时候,也可以在出PQ的时候,在入PQ的时候更新理论上会更快)的时候才把对应的点权更新上去。因为dis[u]的含义是“从s点到u点经过的所有点的点权的最小值”。
上面这个做法会不会是假做法呢?好像是挺假的,群友们也说DAG上跑Dijkstra有问题?我想到了一个反例:
5 5
5 4 2 1 3
1 2 1
1 3 1
2 4 1
4 3 1
3 5 1
这样缩点之后也是完全一样的图,Dijkstra的过程是这样:
取出1号点,把{2,3号}和{4,2号}加入PQ;
取出3号点,把{2,5号}加入PQ;
取出5号点,更新了错误的最小值为2。(因为1->2->4->5才是最小值1,在4号点取得最小值)。
不过虽然Dijkstra跑出了错误的结果,但是我这个假算法的鲁棒性也太强了吧。
构造一个这样的图:
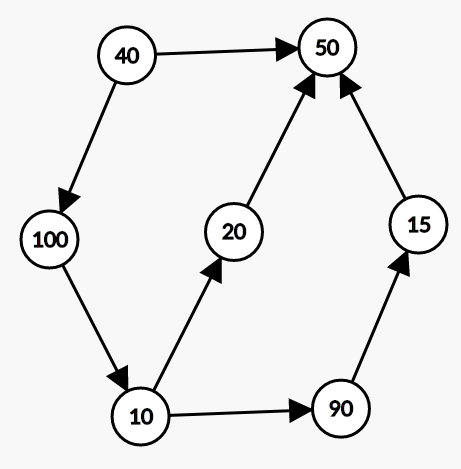
生成好看的图的工具是:https://csacademy.com/app/graph_editor/
这个图里面,计算从40开始的最小价格,Dijkstra会直接把50标记为40,而不是正确的10。反过来计算到达50的最大价格,又会把10标记成20,而不是正确的90。原因是在于Dijkstra被局部的最优情况欺骗了。
对应的数据是:
7 8
40 100 10 20 90 15 50
1 2
1 7
2 3
3 4
3 5
4 7
5 6
6 7
但是好像还是没卡掉,这个假算法的鲁棒性也太强了,因为他甚至会更新已经vis过的节点!也就是说Dijkstra去掉那个跳过已vis节点会更加鲁棒?但是这个算法确实是错的,只需要在正确答案更新其后继节点之前,保证后继节点已经被vis过,那么后继节点的新信息就不会继续传递给其后继节点。
但是缩点之后DP是肯定没有错的,当一个点已经没有任何入边,那么他不可能再进行修改,他的答案也随之确定。
const int MAXN = 1e5;
int n, m;
int price[MAXN + 5];
namespace SCC {
int n;
vector<int> G[MAXN + 5], BG[MAXN + 5];
int c1[MAXN + 5], cntc1;
int c2[MAXN + 5], cntc2;
int s[MAXN + 5], cnts;
int n2;
vector<int> V2[MAXN + 5];
vector<int> G2[MAXN + 5], BG2[MAXN + 5];
void Init(int _n) {
n = _n;
cntc1 = 0, cntc2 = 0, cnts = 0;
for(int i = 1; i <= n; ++i) {
G[i].clear();
BG[i].clear();
c1[i] = 0;
c2[i] = 0;
s[i] = 0;
V2[i].clear();
G2[i].clear();
BG2[i].clear();
}
return;
}
void AddEdge(int u, int v) {
G[u].push_back(v);
BG[v].push_back(u);
return;
}
void dfs1(int u) {
c1[u] = cntc1;
for(auto &v : G[u]) {
if(!c1[v])
dfs1(v);
}
s[++cnts] = u;
}
void dfs2(int u) {
V2[cntc2].push_back(u);
c2[u] = cntc2;
for(auto &v : BG[u]) {
if(!c2[v])
dfs2(v);
}
return;
}
void Kosaraju() {
for(int i = 1; i <= n; ++i) {
if(!c1[i]) {
++cntc1;
dfs1(i);
}
}
for(int i = n; i >= 1; --i) {
if(!c2[s[i]]) {
++cntc2;
dfs2(s[i]);
}
}
return;
}
void Build() {
n2 = cntc2;
for(int i = 1; i <= n2; ++i) {
for(auto &u : V2[i]) {
for(auto &v : G[u]) {
if(c2[v] != i) {
G2[i].push_back(c2[v]);
BG2[c2[v]].push_back(i);
}
}
}
}
for(int i = 1; i <= n2; ++i) {
sort(G2[i].begin(), G2[i].end());
G2[i].erase(unique(G2[i].begin(), G2[i].end()), G2[i].end());
sort(BG2[i].begin(), BG2[i].end());
BG2[i].erase(unique(BG2[i].begin(), BG2[i].end()), BG2[i].end());
}
return;
}
int minV2[MAXN + 5], maxV2[MAXN + 5];
int indeg[MAXN + 5], outdeg[MAXN + 5];
int vis1[MAXN + 5], visn[MAXN + 5];
queue<int> Q;
void DPin() {
while(!Q.empty())
Q.pop();
for(int i = 1; i <= n2; ++i) {
vis1[i] = 0;
indeg[i] = BG2[i].size();
if(indeg[i] == 0)
Q.push(i);
}
while(!Q.empty()) {
int u = Q.front();
Q.pop();
if(c2[1] == u)
vis1[u] = 1;
for(auto &v : G2[u]) {
--indeg[v];
if(indeg[v] == 0)
Q.push(v);
if(vis1[u] == 1) {
minV2[v] = min(minV2[v], minV2[u]);
vis1[v] = 1;
}
}
}
}
void DPout() {
while(!Q.empty())
Q.pop();
for(int i = 1; i <= n2; ++i) {
visn[i] = 0;
outdeg[i] = G2[i].size();
if(outdeg[i] == 0)
Q.push(i);
}
while(!Q.empty()) {
int u = Q.front();
Q.pop();
if(c2[n] == u)
visn[u] = 1;
for(auto &v : BG2[u]) {
--outdeg[v];
if(outdeg[v] == 0)
Q.push(v);
if(visn[u] == 1) {
maxV2[v] = max(maxV2[v], maxV2[u]);
visn[v] = 1;
}
}
}
}
void Solve() {
for(int i = 1; i <= n2; ++i) {
minV2[i] = INF, maxV2[i] = -INF;
for(auto &u : V2[i]) {
minV2[i] = min(minV2[i], price[u]);
maxV2[i] = max(maxV2[i], price[u]);
}
indeg[i] = BG2[i].size();
outdeg[i] = G2[i].size();
}
DPin();
DPout();
int ans = 0;
for(int i = 1; i <= n2; ++i) {
if(vis1[i] == 1 && visn[i] == 1)
ans = max(ans, maxV2[i] - minV2[i]);
}
printf("%d
", ans);
return;
}
}
void TestCase() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i)
scanf("%d", &price[i]);
SCC::Init(n);
for(int i = 1; i <= m; ++i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
SCC::AddEdge(u, v);
if(w == 2)
SCC::AddEdge(v, u);
}
SCC::Kosaraju();
SCC::Build();
SCC::Solve();
return;
}
或者用直接进行正反两次SPFA就可以了,毕竟这个假算法简单又无脑。
收获:
- 假算法甚至也可以通过题目,没招的话可以试试看假一波,假如不是对着我的假算法卡,非常难卡。
- 居然没有故意卡SPFA,正式区域赛不到没招不要上SPFA。