代码覆盖率:
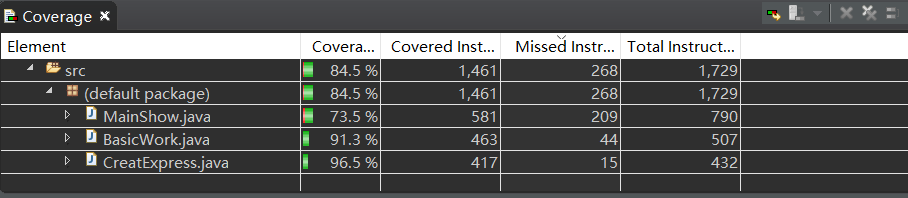
四、设计实现过程
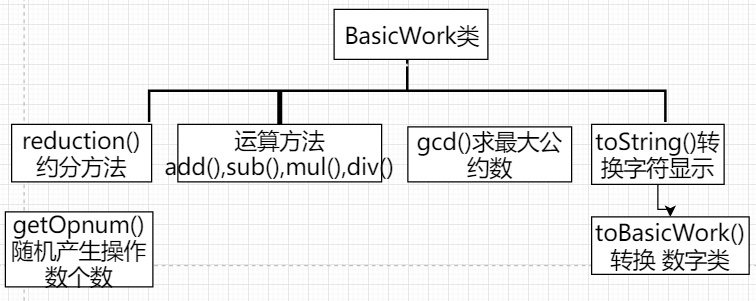
这次的项目需求是自动生成四则运算题目,难点在于随机数的处理和优先级的计算。在阅读完题目并分析需求后,我们先解决的是随机数的生成。因为要求有自然数和真分数,我们用到了一个数字类BasicWork来产生随机数。数字类定义一个数为带分数,分子为零的时候生成一个整数,否则生成一个真分数。这样做的好处是可以将自然数和真分数都统一,在后续的生成和计算过程能够通过调用数字类的方法处理。在数字类中,因为每个随机数都有3个部分组成,我们重新定义了数字类的加减乘除方法。数字类中还包括一个约分方法reduction()对生成的随机数和计算的结果进行处理,确保数字类满足是自然数或真分数的需求。
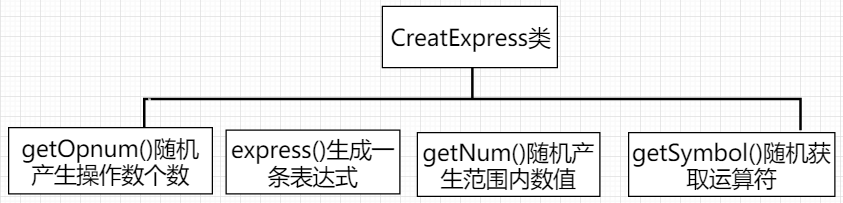
CreatExpress类用来随机生成式子,用一个随机数来决定式子的操作数个数,根据操作数个数随机生成运算符并连接成四则运算表达式。生成括号这一部分的处理,是通过判断括号出现的正确位置来随机生成。
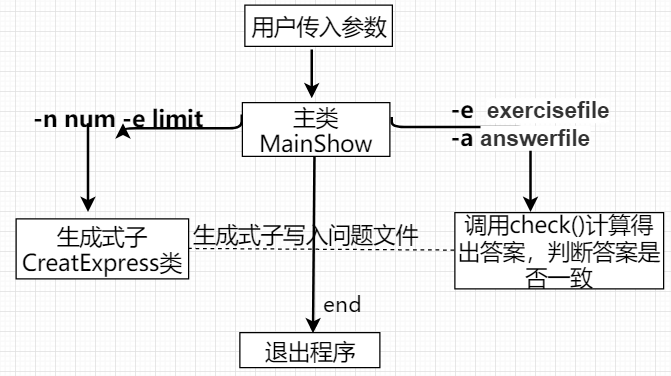
MainShow主类则是显示出相关的使用信息,接收用户传入的参数。实现生成题目文件和答案文件需求的方法写在主类中,循环生成式子的同时把式子逐条写进题目文件里,并计算出答案写进答案文件。判断表达式重复的过程就是判断计算过程是否重复,这里仅仅是判断结果是否相同,不够完善。生成式子时调用主类的check()方法计算得出答案,并判断答案是否一致进行正确统计。
五、代码说明
对表达式字符串逐个字符判断,将操作数与操作符分隔,同时,将原来的中缀表达式转换为后缀表达式进行计算。
对于将中缀表达式转后缀表达式,进行如下操作:从表达式左到右进行操作,如果是数值,将其放入number数组模拟的栈;如果是操作符,判断symbol数组模拟的栈,如果栈为空或栈顶为左括号,操作符直接进栈,如果栈顶为操作符,根据操作符优先级判断,如果栈顶操作符优先级低,操作符直接进栈,否则,将栈顶操作符放入number数组,继续讨论栈顶元素;如果是左括号,直接进栈;如果是右括号,将栈顶操作符放入number数组,直到栈顶为左括号,括号不放入number数组。最后将symbo模拟的栈中剩余操作符取出放入number数组。
于是,我们便得到后缀表达式,对后缀表达式进行计算,从表达式(number数组)左到右进行操作,如果是操作数,放入stk栈;如果是操作符,将stk栈顶2个元素进行计算,再将结果放入stk栈。最后,stk栈剩余一个操作数,便是表达式结果,运算无误则方法返回结果。在计算过程中,判断是否出现负数,如果出现负数方法返回null值,表示表达式不合法。
//判断表达式是否合法,是否重复
public static BasicWork check(String s) {
boolean flag = true;
String symbol[] = new String[100];
int sym = 0;
String number[] = new String[100];
int num = 0;
String str = "";
//计算、判断合法、判断重复
for(int i = 0; i < s.length(); i++) {
if(s.charAt(i) == '+' || s.charAt(i) == '-' || s.charAt(i) == '×' || s.charAt(i) == '÷'
|| s.charAt(i) == '(' || s.charAt(i) == ')') {
if(!str.equals("")) {
number[num++] = str;
str = "";
}
if(s.charAt(i) == '+') {
while(sym != 0 && !symbol[sym-1].equals("(")) {
number[num++] = symbol[sym-1];
sym--;
}
symbol[sym++] = "+";
}
else if(s.charAt(i) == '-') {
while(sym != 0 && !symbol[sym-1].equals("(")) {
number[num++] = symbol[sym-1];
sym--;
}
symbol[sym++] = "-";
}
else if(s.charAt(i) == '×') {
while(sym != 0 && (symbol[sym-1].equals("×") || symbol[sym-1].equals("÷"))) {
number[num++] = symbol[sym-1];
sym--;
}
symbol[sym++] = "×";
}
else if(s.charAt(i) == '÷') {
while(sym != 0 && (symbol[sym-1].equals("×") || symbol[sym-1].equals("÷"))) {
number[num++] = symbol[sym-1];
sym--;
}
symbol[sym++] = "÷";
}
else if(s.charAt(i) == '(') {
symbol[sym++] = "(";
}
else if(s.charAt(i) == ')') {
while(sym != 0 && !symbol[sym-1].equals("(")) {
number[num++] = symbol[sym-1];
sym--;
}
if(sym != 0 && symbol[sym-1].equals("(")) sym--;
}
}
else {
str += s.charAt(i);
}
}
BasicWork tempA, tempB;
if(!str.equals("")) number[num++] = str;
while(sym > 0) {
number[num++] = symbol[sym-1];
sym--;
}
// for(int i = 0; i < num; i++) System.out.print(number[i]+" ");
// System.out.println();
Stack<BasicWork> stk = new Stack<BasicWork>();
for(int i = 0; i < num; i++) {
if(number[i].equals("+")) {
tempA = stk.peek();
stk.pop();
tempB = stk.peek();
stk.pop();
tempA = tempB.add(tempA);
stk.push(tempA);
}
else if(number[i].equals("-")) {
tempA = stk.peek();
stk.pop();
tempB = stk.peek();
stk.pop();
tempA = tempB.sub(tempA);
stk.push(tempA);
if(tempA.zheng < 0 || tempA.fenzi < 0||tempA.fenmu<0) {
flag = false;
break;
}
}
else if(number[i].equals("×")) {
tempA = stk.peek();
stk.pop();
tempB = stk.peek();
stk.pop();
tempA = tempB.mul(tempA);
stk.push(tempA);
}
else if(number[i].equals("÷")) {
tempA = stk.peek();
stk.pop();
tempB = stk.peek();
stk.pop();
if(tempA.zheng == 0 && tempA.fenzi == 0) {
flag = false;
break;
}
tempA = tempB.div(tempA);
stk.push(tempA);
}
else {
stk.push(BasicWork.toBasicWork(number[i]));
}
}
if(flag == false) return null;
else return stk.peek();
}
随机生成一条式子
//生成一条式子
public static String express(int limit,int opnum) {
String str = null;
for(int i=0;i<opnum;i++) {
a[i]=new BasicWork(limit);
BasicWork.reduction(a[i]);
}
if(opnum == 2) {
str = a[0].toString() + getSymbol() + a[1].toString();
}
else if(opnum == 3) {
int randx = (int)(Math.random()*10);
if(randx == 0)
str = "("+a[0].toString() + getSymbol() + a[1].toString() + ")" + getSymbol() + a[2].toString();
else if(randx == 1)
str = a[0].toString() + getSymbol() + "(" + a[1].toString() + getSymbol() + a[2].toString() + ")";
else
str = a[0].toString() + getSymbol() + a[1].toString() + getSymbol() + a[2].toString();
}
else {
int randx = (int)(Math.random()*30);
if(randx == 0)
str = "(" + a[0].toString() + getSymbol() + a[1].toString() + getSymbol() + a[2].toString() + ")"
+ getSymbol() + a[3].toString();
else if(randx == 1)
str = a[0].toString() + getSymbol() + "(" + a[1].toString() + getSymbol() + a[2].toString() + ")"
+ getSymbol() + a[3].toString();
else if(randx == 2)
str = "(" + a[0].toString() + getSymbol() + "(" + a[1].toString() + getSymbol() + a[2].toString() + "))"
+ getSymbol() + a[3].toString();
else if(randx == 3)
str = a[0].toString() + getSymbol() + "(" + a[1].toString() + getSymbol() + "(" + a[2].toString()
+ getSymbol() + a[3].toString() + "))";
else if(randx == 4)
str = "(" + a[0].toString() + getSymbol() + a[1].toString() + ")" + getSymbol() + "(" + a[2].toString()
+ getSymbol() + a[3].toString() + ")";
else
str = a[0].toString() + getSymbol() + a[1].toString() + getSymbol() + a[2].toString()
+ getSymbol() + a[3].toString();
}
return str;
}
数字类BasicWork
public class BasicWork {
int fenzi;
int fenmu;
int zheng;
public BasicWork() {
}
public BasicWork(int limit) {
// fenzi=(int)(0+Math.random()*(limit-0+1));
// zheng=(int)(0+Math.random()*(limit-0+1));
zheng=0;
fenmu=(int)(1+Math.random()*(limit-1+1));
fenzi=(int)(Math.random()*fenmu*limit);
reduction(this);
}
//用于测试
public BasicWork(int a,int b,int c) {
fenzi=a;
fenmu=b;
zheng=c;
}
//约分方法
public static void reduction(BasicWork reop) {
int re=gcd(reop.fenzi,reop.fenmu);
re = re == 0 ? 1 : re;
reop.fenzi=reop.fenzi/re;
reop.fenmu=reop.fenmu/re;
//System.out.println(reop.fenzi + " " + reop.fenmu);
try {
if(reop.fenzi>=reop.fenmu) {
reop.zheng=reop.zheng+reop.fenzi/reop.fenmu;
reop.fenzi=reop.fenzi%reop.fenmu;
if(reop.fenzi==0) reop.fenmu=1;
}
} catch (Exception e) {
e.printStackTrace();
}
}
public BasicWork add(BasicWork a) {
BasicWork temp=new BasicWork();
temp.zheng=zheng+a.zheng;
temp.fenmu=fenmu*a.fenmu;
temp.fenzi=fenzi*a.fenmu+a.fenzi*fenmu;
//约分
reduction(temp);
return temp;
}
public BasicWork sub(BasicWork s) {
BasicWork temp=new BasicWork();
temp.fenzi=fenzi+fenmu*zheng;
temp.zheng=0;
temp.fenmu=fenmu;
s.fenzi=s.fenzi+s.fenmu*s.zheng;
s.zheng=0;
temp.fenzi=temp.fenzi*s.fenmu;
s.fenzi=s.fenzi*temp.fenmu;
temp.fenmu=temp.fenmu*s.fenmu;
temp.fenzi=temp.fenzi-s.fenzi;
//约分
reduction(temp);
return temp;
}
public BasicWork mul(BasicWork m) {
BasicWork temp=new BasicWork();
temp.fenzi=fenzi+fenmu*zheng;
temp.zheng=0;
temp.fenmu=fenmu;
m.fenzi=m.fenzi+m.fenmu*m.zheng;
m.zheng=0;
temp.fenmu=temp.fenmu*m.fenmu;
temp.fenzi=temp.fenzi*m.fenzi;
//约分
reduction(temp);
return temp;
}
public BasicWork div(BasicWork d) {
d.fenzi+=d.fenmu*d.zheng;
d.zheng=0;
int i;
i=d.fenmu;
d.fenmu=d.fenzi;
d.fenzi=i;
return this.mul(d);
}
public boolean equals(BasicWork rhs) {
return (zheng*fenmu+fenzi)*rhs.fenmu == (rhs.zheng*rhs.fenmu+rhs.fenzi)*fenmu;
}
private static int gcd(int a,int b) {
if(b==0) return a;
return gcd(b,a%b);
}
public String toString() {
String s=new String();
if(fenzi==0) s=zheng+"";
else if(zheng==0) s=fenzi+"/"+fenmu;
else s=zheng+"'"+fenzi+"/"+fenmu;
return s;
}
//命令行传入参数转换为整型
public static int toInt(String s) {
int ans=0;
for(int i=0;i<s.length();i++) {
ans=ans*10+s.charAt(i)-'0';
}
return ans;
}
public static BasicWork toBasicWork(String str) {
BasicWork temp = new BasicWork();
ArrayList<Integer> ary = new ArrayList<Integer>();
int tmp = 0;
for(int i = 0; i < str.length(); i++) {
if(str.charAt(i) >= '0' && str.charAt(i) <= '9') tmp = tmp*10+str.charAt(i)-'0';
else {
ary.add(tmp);
tmp = 0;
}
}
ary.add(tmp);
if(ary.size() == 1) {
temp.zheng = ary.get(0);
temp.fenzi = 0;
temp.fenmu = 1;
}
else if(ary.size() == 2) {
temp.zheng = 0;
temp.fenzi = ary.get(0);
temp.fenmu = ary.get(1);
}
else {
temp.zheng = ary.get(0);
temp.fenzi = ary.get(1);
temp.fenmu = ary.get(2);
}
return temp;
}
}
六、测试运行
测试-n -r


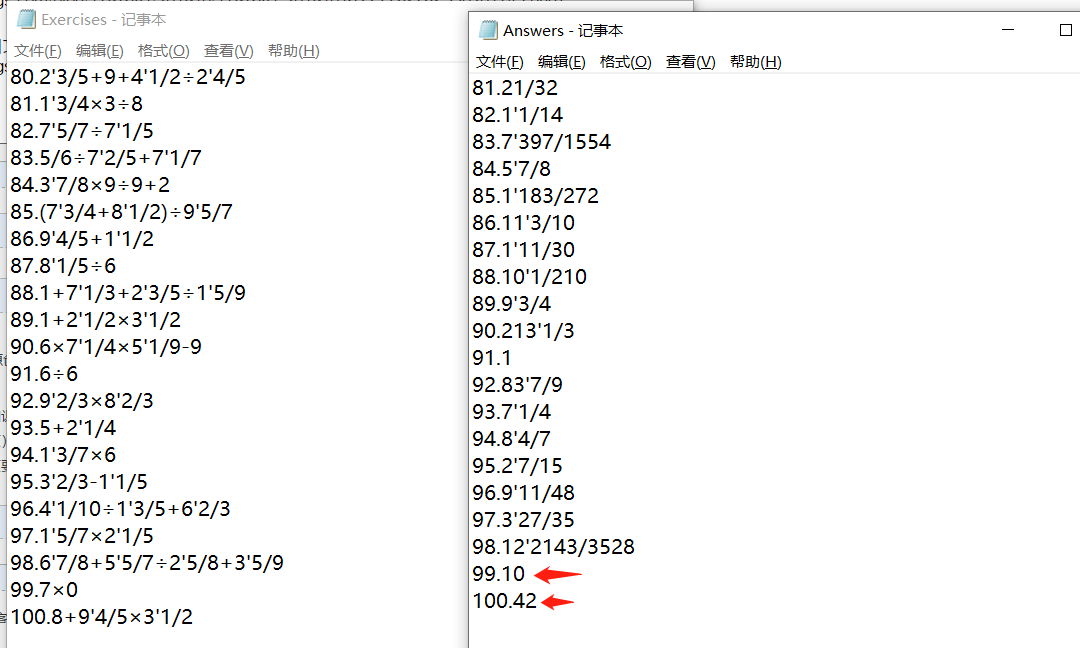
测试-e -a
这里选用刚刚生成的题目文件和答案文件,答案文件修改几个答案以验证功能



生成10000条题目
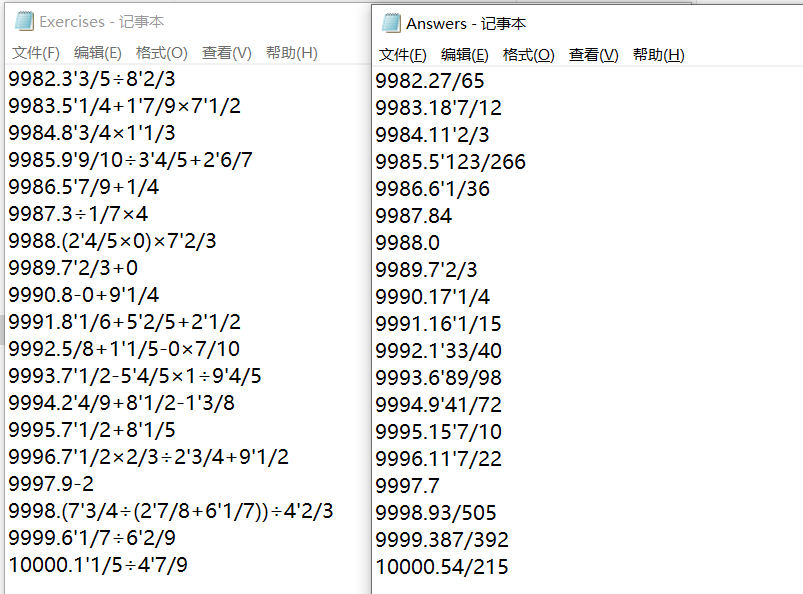
经验证,功能正确实现。
七、项目小结
- 这次的核心是数字类和转换为后缀表达式去计算答案。数字类将操作数封装成类,在后续的操作中会简单很多,而且代码更简洁易懂。
- 初次使用结对编程这种软件开发的方法开发项目,受益匪浅,2个人若是能很好磨合,将达到事半功倍的效果。打代码过程互相鼓励,互相监督,比起自己一个人打代码更有激情。