1 归一化处理
归一化是一种数理统计中常用的数据预处理手段,在机器学习中归一化通常将数据向量每个维度的数据映射到(0,1)或(-1,1)之间的区间或者将数据向量的某个范数映射为1,归一化好处有两个:
(1) 消除数据单位的影响:其一可以将有单位的数据转为无单位的标准数据,如成年人的身高150-200cm、成年人体重50-90Kg,身高的单位是厘米而体重的单位是千克,不同维度的数据单位不一样,造成原始数据不能直接代入机器学习中进行处理,所以这些数据经过特定方法统一都映射到(0,1)这个区间,这样所有数据的取值范围都在同一个区间里的。
(2) 可提深度学习模型收敛速度: 如果不进行归一化处理,假设深度学习模型接受的输入向量只有两个维度x1和x2,其中X1取值为0-2000,x2取值为0-3。这样数据在进行梯度下降计算时梯度时对应一个很扁的椭圆形,很容易在垂直等高线的方向上走大量的之字形路线,是的迭代计算量大且迭代的次数多,造成深度学习模型收敛慢。
2 L2范数归一化的概念
L2范数归一化处理操作是对向量X的每个维度数据x1, x2, …, xn都除以||x||2得到一个新向量,即
[{{�f{X}}_2} = left( {frac{{{x_1}}}{{{{left| {�f{x}}
ight|}_2}}},frac{{{x_2}}}{{{{left| {�f{x}}
ight|}_2}}}, cdots ,frac{{{x_n}}}{{{{left| {�f{x}}
ight|}_2}}}}
ight) = left( {frac{{{x_1}}}{{sqrt {x_1^2 + x_2^2 + cdots + x_n^2} }},frac{{{x_2}}}{{sqrt {x_1^2 + x_2^2 + cdots + x_n^2} }}, cdots ,frac{{{x_n}}}{{sqrt {x_1^2 + x_2^2 + cdots + x_n^2} }}}
ight)
]
若向量A = (2, 3, 6),易得向量X的L2范数为
[{left| {�f{A}}
ight|_2} = sqrt {{2^2} + {3^2} + {6^2}} = sqrt {4 + 9 + 36} = sqrt {49} = 7
]
所以向量A的L2范数归一化后得到向量为
[{{�f{A}}_2} = left( {frac{2}{7},frac{3}{7},frac{6}{7}}
ight)
]
图1 L2范数可以看作是向量的长度
3 L2范数归一化的优势
L2范数有一大优势:经过L2范数归一化后,一组向量的欧式距离和它们的余弦相似度可以等价
一个向量X经过L2范数归一化得到向量X2,同时另一个向量Y经过L2范数归一化得到向量Y2。此时X2和Y2的欧式距离和余弦相似度是等价的,下面先给出严格的数学证明。
假设向量X = (x1, x2, …, xn),向量Y = (y1, y2, …, yn), X2和Y2的欧式距离是
[�egin{array}{l}
Dleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight) = sqrt {{{left( {frac{{{x_1}}}{{{{left| {�f{X}}
ight|}_2}}} - frac{{{y_1}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^2} + {{left( {frac{{{x_2}}}{{{{left| {�f{X}}
ight|}_2}}} - frac{{{y_2}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^2} + cdots + {{left( {frac{{{x_n}}}{{{{left| {�f{X}}
ight|}_2}}} - frac{{{y_n}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^2}} \
quad quad quad quad quad ;;; = sqrt {left( {frac{{�f{X}}}{{{{left| {�f{X}}
ight|}_2}}} - frac{{�f{Y}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight){{left( {frac{{�f{X}}}{{{{left| {�f{X}}
ight|}_2}}} - frac{{�f{Y}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^T}} \
quad quad quad quad quad ;;; = sqrt {frac{{{�f{X}}{{�f{X}}^T}}}{{left| {�f{X}}
ight|_2^2}} - frac{{{�f{X}}{{�f{Y}}^T}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}} - frac{{{�f{Y}}{{�f{X}}^T}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}} + frac{{{�f{Y}}{{�f{Y}}^T}}}{{left| {�f{Y}}
ight|_2^2}}} \
quad quad quad quad quad ;;; = sqrt {frac{{{�f{X}}{{�f{X}}^T}}}{{{�f{X}}{{�f{X}}^T}}} - frac{{2{�f{X}}{{�f{Y}}^T}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}} + frac{{{�f{Y}}{{�f{Y}}^T}}}{{{�f{Y}}{{�f{Y}}^T}}}} \
quad quad quad quad quad ;;; = sqrt {2 - 2frac{{{�f{X}}{{�f{Y}}^T}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}}} \
end{array}]
X2和Y2的余弦相似度为
[�egin{array}{l}
Simleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight) = frac{{frac{{{x_1}}}{{{{left| {�f{X}}
ight|}_2}}} cdot frac{{{y_1}}}{{{{left| {�f{Y}}
ight|}_2}}}{
m{ + }}frac{{{x_{
m{2}}}}}{{{{left| {�f{X}}
ight|}_2}}} cdot frac{{{y_{
m{2}}}}}{{{{left| {�f{Y}}
ight|}_2}}}{
m{ + }} cdots {
m{ + }}frac{{{x_n}}}{{{{left| {�f{X}}
ight|}_2}}} cdot frac{{{y_n}}}{{{{left| {�f{Y}}
ight|}_2}}}}}{{sqrt {{{left( {frac{{{x_1}}}{{{{left| {�f{X}}
ight|}_2}}}}
ight)}^{
m{2}}}{
m{ + }}{{left( {frac{{{x_{
m{2}}}}}{{{{left| {�f{X}}
ight|}_2}}}}
ight)}^{
m{2}}}{
m{ + }} cdots {{left( {frac{{{x_{
m{n}}}}}{{{{left| {�f{X}}
ight|}_2}}}}
ight)}^{
m{2}}}} cdot sqrt {{{left( {frac{{{y_1}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^{
m{2}}}{
m{ + }}{{left( {frac{{{y_{
m{2}}}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^{
m{2}}}{
m{ + }} cdots {
m{ + }}{{left( {frac{{{y_n}}}{{{{left| {�f{Y}}
ight|}_2}}}}
ight)}^{
m{2}}}} }} \
quad quad quad quad quad ;;; = frac{{frac{{{x_1}{y_1} + {x_2}{y_2} + cdots + {x_n}{y_n}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}}}}{{sqrt {frac{{x_1^2 + x_2^2 + cdots + x_n^2}}{{left| {�f{X}}
ight|_2^2}}} cdot sqrt {frac{{y_1^2 + y_2^2 + cdots y_n^2}}{{left| {�f{Y}}
ight|_2^2}}} }} \
quad quad quad quad quad ;;; = frac{{frac{{{x_1}{y_1} + {x_2}{y_2} + cdots + {x_n}{y_n}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}}}}{{sqrt {frac{{x_1^2 + x_2^2 + cdots + x_n^2}}{{x_1^2 + x_2^2 + cdots + x_n^2}}} cdot sqrt {frac{{y_1^2 + y_2^2 + cdots y_n^2}}{{y_1^2 + y_2^2 + cdots y_n^2}}} }} \
quad quad quad quad quad ;;; = frac{{{x_1}{y_1} + {x_2}{y_2} + cdots + {x_n}{y_n}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}} \
quad quad quad quad quad ;;; = frac{{{�f{X}}{{�f{Y}}^T}}}{{{{left| {�f{X}}
ight|}_2}{{left| {�f{Y}}
ight|}_2}}} \
end{array}]
结合两个表达式易得
[Dleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight) = sqrt {2 - 2simleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight)}
]
即L2范数归一化处理后两个向量欧式距离等于2减去2倍余弦相似度的算术平方根。如果你被上面令人昏头转向的数学公式搞晕,而不想看的话,这里还有一种仅需要中学知识的更简单证明方法证明两者的等价性:
假设一组二维数据,设经过L2范数归一化后向量X2 为 (p1, p2),向量Y2 为 (q1, q2)。向量X2是原点(0,0) 指向点P(p1,p2)的有向线段,向量Y2是原点(0,0)指向点Q(q1, q2)的有向线段。易得
X2和Y2的欧式距离为线段PQ长度
X2和Y2的余弦相似度为∠POQ的余弦值
根据余弦定理易得
[cos angle POQ = frac{{O{P^2} + O{Q^2} - P{Q^2}}}{{2 cdot OP cdot OQ}}
]
因为L2范数归一化向量的长度都是1,因为L2范数归一化向量的长度都是1,那么向量对应的点肯定都在单位圆上,所以OP=OQ=1
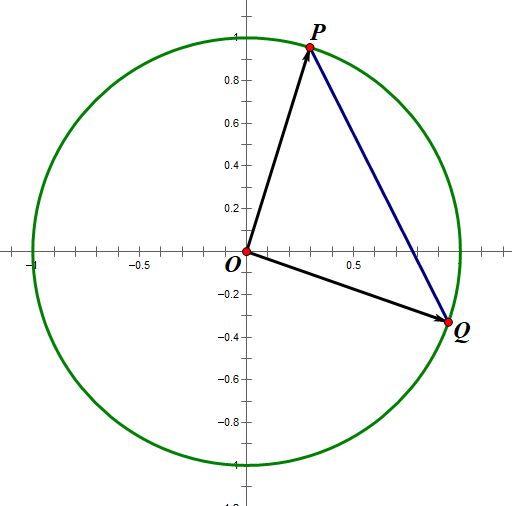
图2 L2范数归一化后向量对应的点都在单位圆上
因此
[cos angle POQ = frac{{{1^2} + {1^2} - P{Q^2}}}{2} = frac{{2 - P{Q^2}}}{2}
]
即
[simleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight) = frac{{2 - D{{left( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight)}^2}}}{2} Rightarrow Dleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight) = sqrt {2 - 2simleft( {{{�f{X}}_{
m{2}}},{{�f{Y}}_{
m{2}}}}
ight)}
]
因此经L2范数归一化后,一组向量的欧式距离和它们的余弦相似度可等价。这一大优势是当你算得一组经过L2范数归一化后的向量的欧式距离后,又想计算它们的余弦相似度,可以根据公式在O(1)时间内直接计算得到;反过来也一样。
另外,在一些机器学习处理包中,只有欧式距离计算没有余弦相似度计算,如Sklearn的Kmeans聚类包,这个包只能处理欧式距离计算的数据聚类。
而在NLP领域,许多词语或文档的相似度定义为数据向量的余弦相似度,如果直接调用Sklearn的Kmeans聚类包则不能进行聚类处理。因此需要将词语对象的词向量或者文档对应的文本向量进行L2范数归一化处理。因为在L2范数归一化处理后的欧式距离和余弦相似度是等价的,所以此时可以放心大胆用Sklearn的Kmeans进行聚类处理。

