欧拉回路就是用一笔走过所有的路,现在让你判断到底有几个欧拉回路,也就是说走一个图需要用几笔。
首先根据给出的边我们只需要分别处理每个连通分量需要多少笔即可.
如果该连通分量是一个孤立的点,显然只需要0笔.
如果该连通分量是一个欧拉图或半欧拉图,只需要1笔.
现在关键是连通分量并非一个(半)欧拉图时,需要几笔?
一般性的结论是:
非(半)欧拉图需要的笔数==该图中奇数度的点数目/2
下面来证明该结论:
首先一个无向图的连通分量中的奇数度的点个数一定是偶数个(成对出现),因为无向图的总度数=偶数.
我们在这种连通分量中每次画一笔有两种选择:
1.a->b->c->d…->g 一条起点与终点不同的路径(路中除首尾度减1外,每个点度减2)
2.a->b->c->d…->a 一条起点与终点相同的回路(路中每个点度数减2)
也就是说想要把非(半)欧拉图分量中的奇数度的点的度数都变成偶数,我们至少需要画奇数度点个数/2 笔.
那么对于这种图我们最多需要画的笔数 是不是也是 : 奇数度点个数/2 笔呢?
答案是肯定的,这里假设图中有4个奇数度的点,1,2,3,4,5,6.如下图所示:
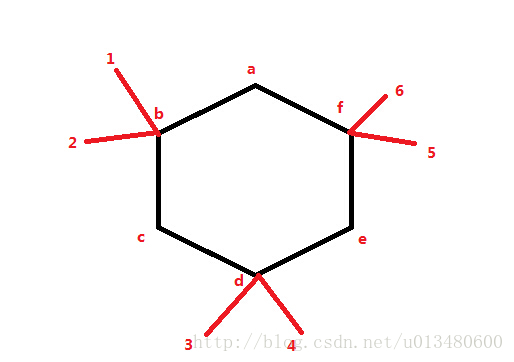
我们先走路:1-> b-> c-> d-> e-> f->a-> 2 这条路.然后6,5 和3,4 分别属于两个连通分量了.可以看出只需要3笔,即6/2=3即可.
也就是说对于这种非(半)欧拉图的连通分量,我们每笔必然消除正好2个点的奇度(使其度变偶数),当最后一笔的时候我们必然消除所有的点的度数(包括剩下的两个奇点,因为最后一笔就必然是欧拉通路).但是有一点要注意,有可能过程中的某几笔会使得该连通分量变成多个连通分量,当然结论不变.
经过上面的分析,这题的结论出来了,对于每个以i为根的连通分量我们记录属于该连通分量的点数目num[i]和该连通分量中奇度点的个数odd[i].
如果num[i]==0或1,需0笔.(注意num[i]==0表示i点不是根,num[i]==1表示i点是一个孤立的点.)
如果num[i]>1且odd[i]==0 需1笔
如果num[i]>1且odd[i]>0 需odd[i]/2笔

1 #include<iostream> 2 #include<cstdio> 3 #include<string> 4 #include<cstring> 5 #include<map> 6 #include<set> 7 #include<vector> 8 #include<queue> 9 #include<algorithm> 10 #include<cmath> 11 using namespace std; 12 #define ll long long 13 const int N = 100000 + 10; 14 int n, m,xx,yy; 15 int fa[N], indu[N], odd[N],num[N]; 16 int find(int x) 17 { 18 if (fa[x] == -1) return x; 19 return fa[x] = find(fa[x]); 20 } 21 void hebing(int a, int b) 22 { 23 a = find(a); 24 b = find(b); 25 if(a!=b) 26 fa[a] = b; 27 } 28 int main() 29 { 30 while (scanf("%d %d", &n, &m) != EOF) 31 { 32 memset(fa, -1, sizeof(fa)); 33 memset(indu, 0, sizeof(indu)); 34 memset(odd, 0, sizeof(odd)); 35 memset(num, 0, sizeof(num)); 36 while (m--) 37 { 38 scanf("%d %d",&xx,&yy); 39 indu[xx]++; 40 indu[yy]++; 41 hebing(xx, yy); 42 } 43 for (int i = 1; i <= n; i++) 44 { 45 num[find(i)]++; 46 if (indu[i] % 2 == 1) 47 odd[find(i)]++; 48 } 49 int ans = 0; 50 for (int i = 1; i <= n; i++) 51 { 52 if (num[i] <= 1) continue; 53 if (odd[i] == 0) ans += 1; 54 else ans += odd[i] / 2; 55 } 56 printf("%d ",ans); 57 } 58 59 return 0; 60 }
