首先利用组合数学知识,枚举两人的总胜场数容易得到
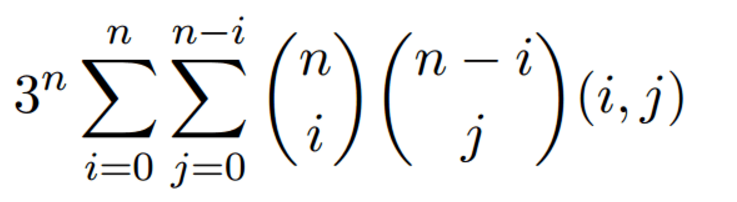
这还不是卷积的形式,直接搞的话复杂度大概是O(n^2)的,肯定会TLE。但似乎和卷积有点像?想半天没想出来。。多谢Q巨提醒,才知道可以用下面这个公式进行转化

最后,化得的公式为
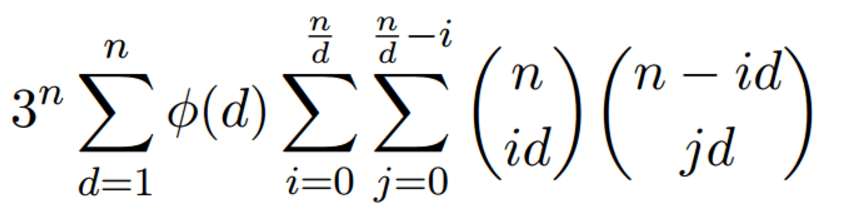
另外注意,上式右边是一个卷积的形式,但是,所得和的第一项是不需要加上的(不过图中公式没有体现)。结合实际意义大概就是,i==0&&j==0时,gcd(i,j)不存在约数d,虽然0可以被任意正整数整除 & 第一项不为0
#include<bits/stdc++.h> using namespace std; typedef long long LL; typedef double db; #define upmo(a,b) (((a)=((a)+(b))%mod)<0?(a)+=mod:(a)) // 相加后取模 int n,mod; namespace FFT_MO //前面需要有 mod(1e8~1e9级别),upmo(a,b) 的定义 { const int FFT_MAXN=1<<18; const db pi=3.14159265358979323846264338327950288L; struct cp { db a,b; cp(double a_=0,double b_=0) { a=a_,b=b_; } cp operator +(const cp&rhs)const { return cp(a+rhs.a,b+rhs.b); } cp operator -(const cp&rhs)const { return cp(a-rhs.a,b-rhs.b); } cp operator *(const cp&rhs)const { return cp(a*rhs.a-b*rhs.b,a*rhs.b+b*rhs.a); } cp operator !()const { return cp(a,-b); } }nw[FFT_MAXN+1],f[FFT_MAXN],g[FFT_MAXN],t[FFT_MAXN]; //a<->f,b<->g,t<~>c int bitrev[FFT_MAXN]; void fft_init() //初始化 nw[],bitrev[] { int L=0;while((1<<L)!=FFT_MAXN) L++; for(int i=1;i<FFT_MAXN;i++) bitrev[i]=bitrev[i>>1]>>1|((i&1)<<(L-1)); for(int i=0;i<=FFT_MAXN;i++) nw[i]=cp((db)cosl(2*pi/FFT_MAXN*i),(db)sinl(2*pi/FFT_MAXN*i)); } // n已保证是2的整数次幂 // flag=1:DFT | flag=-1: IDFT void dft(cp *a,int n,int flag=1) { int d=0;while((1<<d)*n!=FFT_MAXN) d++; for(int i=0;i<n;i++) if(i<(bitrev[i]>>d)) swap(a[i],a[bitrev[i]>>d]); // NOTICE! for(int l=2;l<=n;l<<=1) { int del=FFT_MAXN/l*flag; // 决定 wn是在复平面是顺时针还是逆时针变化,以及变化间距 for(int i=0;i<n;i+=l) // ????????????????? { cp *le=a+i,*ri=a+i+(l>>1); // ????????????????? cp *w=flag==1? nw:nw+FFT_MAXN; // 确定wn的起点 for(int k=0;k<(l>>1);k++) { cp ne=*ri * *w; *ri=*le-ne,*le=*le+ne; le++,ri++,w+=del; } } } if(flag!=1) for(int i=0;i<n;i++) a[i].a/=n,a[i].b/=n; } // convo(a,n,b,m,c) a[0..n]*b[0..m] -> c[0..n+m] void convo(LL *a,int n,LL *b,int m,LL *c) { for(int i=0;i<=n+m;i++) c[i]=0; int N=2;while(N<=n+m) N<<=1; // N是c扩展后的长度 for(int i=0;i<N;i++) //扩展 a[],b[] ,存入f[],g[],注意取模 { LL aa=i<=n?a[i]:0,bb=i<=m? b[i]:0; aa%=mod,bb%=mod; f[i]=cp(db(aa>>15),db(aa&32767)); g[i]=cp(db(bb>>15),db(bb&32767)); } dft(f,N),dft(g,N); for(int i=0;i<N;i++) // 频域求积 // ????????????????? { int j=i? N-i:0; t[i]=((f[i]+!f[j])*(!g[j]-g[i])+(!f[j]-f[i])*(g[i]+!g[j]))*cp(0,0.25); } dft(t,N,-1); for(int i=0;i<=n+m;i++) upmo(c[i],(LL(t[i].a+0.5))%mod<<15); for(int i=0;i<N;i++) // 频域求积 // ????????????????? { int j=i? N-i:0; t[i]=(!f[j]-f[i])*(!g[j]-g[i])*cp(-0.25,0)+cp(0,0.25)*(f[i]+!f[j])*(g[i]+!g[j]); } dft(t,N,-1); for(int i=0;i<=n+m;i++) upmo(c[i],LL(t[i].a+0.5)+(LL(t[i].b+0.5)%mod<<30)); } } //==============预处理阶乘及阶乘逆元============== LL qpow(LL x,LL n) //求x^n%mod { LL ret=1; for(; n; n>>=1) { if(n&1) ret=ret*x%mod; x=x*x%mod; } return ret; } LL inv(LL x) { return qpow(x,mod-2); } const LL M=1e5+5; LL fac[M+5]; //阶乘 LL inv_of_fac[M+5]; //阶乘的逆元 void init_fac() { fac[0]=1; for(int i=1; i<=M; i++) fac[i]=fac[i-1]*i%mod; inv_of_fac[M]=qpow(fac[M],mod-2); for(int i=M-1; i>=0; i--) inv_of_fac[i]=inv_of_fac[i+1]*(i+1)%mod; } //================================================ //===================phi(x)打表=================== const int maxn=100007; int phi[maxn+5]; void init_phi() { memset(phi,0,sizeof(phi)); //初始化为0 phi[1]=1; for(int i=2; i<=maxn; i++) { if(!phi[i]) //当i是质数时 for(int j=i; j<=maxn; j+=i) //筛选所有因子为i的数 { if(!phi[j]) phi[j]=j; //若未赋值过,先初始化 phi[j]=phi[j]/i*(i-1); //i是质因数(1-1/i)=(i-1)/i,先除再乘是为了防止越界。 } } } //================================================ LL a[1<<18|1],b[1<<18|1],c[1<<18|1]; int main() { init_phi();FFT_MO::fft_init(); //=============debug============== // int n,m; // mod=1e9+7; // while(cin>>n>>m) // { // for(int i=0;i<=n;i++) cin>>a[i]; // for(int i=0;i<=m;i++) cin>>b[i]; // FFT_MO::convo(a,n,b,m,c); // for(int i=0;i<=n+m;i++) // cout<<c[i]<<' '; // puts(""); // } //================================ int T;scanf("%d",&T); while(T--) { scanf("%d%d",&n,&mod); init_fac(); LL ans=0; for(int d=1;d<=n;d++) { int N=n/d; for(int i=0;i<=N;i++) a[i]=b[i]=inv_of_fac[i*d]; FFT_MO::convo(a,N,b,N,c); LL temp=0; for(int i=1;i<=N;i++) temp=(temp+c[i]*inv_of_fac[n-i*d])%mod; ans=(ans+temp*phi[d])%mod; } ans=ans*fac[n]%mod*qpow(3,n)%mod; printf("%lld ",ans); } }