再生希尔伯特空间与核函数讲解

再生希尔伯特空间与核函数讲解

空间

空间的概念就是 空间 = 集合 + 结构

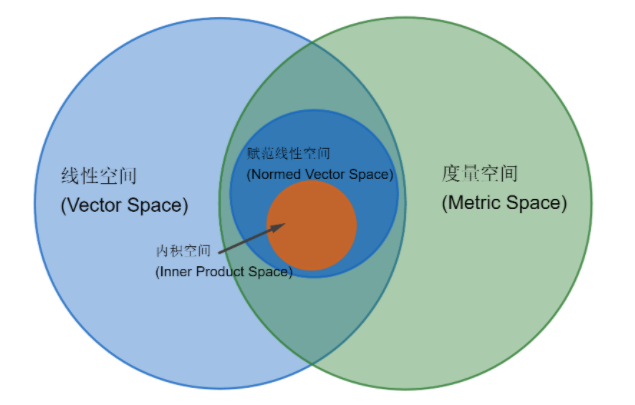
线性空间/向量空间(Linear Space/Vector Space)

线性空间就是 线性空间 = 集合 + 线性结构 ，而其中的线性结构就是 线性结构 = 加法 + 数乘

简单说线性空间就是一系列向量的集合并且只满足加法和标量乘（向量的相乘）操作的集合。

加法运算：首先设一个集合(V),在集合(V)中定义元素的加法运算：(forall x,yin V),在(V)中都有唯一的一个元素(gamma)与之对应，称为(x与y)的和，即(x+y).

数乘运算：数乘就是用一个数字去乘，这个数字的来源就是一个数域(F)，(forall a in F, x in V,)在(V)中都有唯一的元素(delta)与之对应，称为(a与x)的数量乘积

除了运算，以上的两种运算还要满足下面的八种性质：

加法

(x+(y+z) = (x+y)+z)
(x+y = y+x)
存在一个元素(0in V),使得(x+0 = x)，(forall x in V)
(forall x in V),存在一个元素(-xin V),使得(x+(-x) = 0).

数乘

(1x = x)
((ab)x=a(bx))

二者都有：

((a+b)x=ax+bx)
(a(x+y)=ax+ay)

满足以上条件，则称V是数域F上的线性空间或者向量空间，V中的元素称为向量。

度量空间

度量空间 = 集合 + 拓扑结构

给定一个集合(V)，在(V)上定义一种新的运算：距离：(V imes V ightarrow R,forall x,y in V,)在(R)中都有唯一的元素(delta)与之对应，称为(x,y)之间的距离。

满足的性质：

(d(x,y)geqslant0,forall x,y in V)且(d(x,y)=0Leftrightarrow x=y)（非负性）
(d(x,y)leqslant d(x,y)+d(y,z))（三角不等式）
(d(x,y)=d(y,x))（自反性）

其中((V,d))为度量空间或者距离空间，其中V的元素称为点。

赋范线性空间/范数向量空间

赋范线性空间 = 线性空间 + 范数 ：就是给线性空间穿上拓扑结构的外衣。

设(V)是一个实线性空间，对应的数域为(R)，在其上定义范数运算(Vert·Vert:V ightarrow R,)即(forall x in V,)在(R)中都有唯一的元素(delta)与之对应，称之为x的范数，记为(Vert xVert)。

满足的性质：

(Vert xVert geqslant 0)且(Vert xVert = 0 Leftrightarrow x=0)（非负性）
(Vert axVert = vert avert Vert x Vert, ain R)（齐次性）
(Vert x+yVert leqslant Vert xVert + Vert yVert, x,yin V)（三角不等式）

则称((V,Vert ·Vert))为赋范线性空间。

如果我们使用范数来定义距离，即令(d(x,y)=Vert x-yVert),则

(d(x,y)geqslant0,forall x,yin V)且(d(x,y)=0Leftrightarrow x=y)
(d(x,y) = Vert x-z Vert = Vert x-y+y-zVert leqslant Vert x-yVert+Vert y-zVert=d(x,y)+d(y,z))

所以d是V上的距离，((V,d))是度量空间，赋范线性空间V也具有拓扑结构。

距离与范数的关系

距离是空间中任意两点(x,y)满足以下三个条件：

(d(x,y)geqslant0,forall x,y in V)且(d(x,y)=0Leftrightarrow x=y)
(d(x,y)leqslant d(x,y)+d(y,z))
(d(x,y)=d(y,x))

而范数则是空间中的一点到空间零点的距离，满足以下条件：

(Vert xVert geqslant 0)且(Vert xVert = 0 Leftrightarrow x=0)
(Vert axVert = vert avert Vert x Vert, ain R)
(Vert x+yVert leqslant Vert xVert + Vert yVert, x,yin V)

可以看出范数是在距离的基础上添加了新的约束限制，所以范数与距离的关系可以类似理解为与红富士苹果与苹果的关系。

内积空间(inner product space)

内积空间 = 线性空间 + 内积

给定一个集合(V)，在(V)上定义一种新的运算：内积：(V imes V ightarrow R,forall x,y in V,)在(R)中都有唯一的元素(delta)与之对应，称为(x,y)之间的内积，记为((x,y))。

满足性质：

((x,y)geqslant0)且((x,x)=0Leftrightarrow x=0)
((x,y)=(y,x))
((ax,z)=a(x,z),ain R)
((x+y,z)=(x,z)+(y,z))

则((V,(·,·)))为内积空间。

如果使用内积定义范数，令(Vert x Vert=sqrt{(x,x)})，则

(Vert xVertgeqslant 0)且(Vert xVert=0 Leftrightarrow 0)
(Vert axVert=sqrt{(ax,ax)}=sqrt{a^2(x,x)}=vert avertVert xVert)

则(Vert x Vert=sqrt{(x,x)})是线性空间V上的范数，(V,sqrt{(·,·)})是赋范线性空间。

欧式空间/欧几里得空间(Euclidean Space)

设(V)是实数域(R)上的线性空间（或称为向量空间），若(V)上定义着正定对称双线性型(g)（(g)称为内积），则(V)称为（对于(g)的）内积空间或欧几里德空间（有时仅当(V)是有限维时，才称为欧几里德空间）。这些数学空间可以被扩展来应用于任何有限维度，而这种空间叫做(n)维欧几里得空间（甚至简称(n)维空间）或有限维实内积空间。
欧里几何空间可以说是内积空间的引申。

巴拿赫空间

巴拿赫空间 = 赋范空间 + 完备性

希尔伯特空间

在内积空间上扩展，使得内积空间满足完备性，形成希尔伯特空间如下：

希尔伯特空间 = 内积空间 + 完备性

其中完备性的意思就是空间中的极限运算不能跑出该空间，如有理数空间中的(sqrt{2})的小数表示，其极限随着小数位数的增加收敛到(sqrt{2})，但(sqrt{2})属于无理数，并不在有理数空间，故不满足完备性。

一个通俗的理解是把学校理解为一个空间，你从学校内的宿舍中开始一直往外走，当走不动停下来时（极限收敛），发现已经走出学校了（超出空间），不在学校范围内了（不完备了）。希尔伯特就相当于地球，无论你怎么走，都还在地球内（飞出太空除外）。

希尔伯特空间是一个函数空间，即空间中每个元素都是一个函数。

核函数

1.矩阵的特征值分解

在一般的欧氏空间中，我们可以定义一个(n imes n)的矩阵的特征值和特征向量。

[Amathbf{x}=lambda mathbf{x} ]

其中(lambda)是矩阵(A)的特征值，而(mathbf{x})则是对应的特征向量。如果(A)有两个不同的特征值(lambda_1)与(lambda_2),对应不同的特征向量(mathbf{x_1})与(mathbf{x_2}),且(lambda_1 eqlambda_2),则有

[lambda_1mathbf{x}^T_1mathbf{x}_2=mathbf{x}^T_1A^Tmathbf{x}_2=mathbf{x}^T_1Amathbf{x}_2=lambda_2mathbf{x}^T_1mathbf{x}_2 ]

但是由于(lambda_1 eqlambda_2)，那么一定有(mathbf{x}^T_1mathbf{x}_2=0)，即(mathbf{x_1})与(mathbf{x_2})正交，即两个特征向量是正交的。

对于矩阵(Ain mathcal{R}^{n imes n}),可以找到n个特征值及其对应的特征向量。则A可以按照下面的形式进行特征值分解

[A=QDQ^T ]

其中(Q)为正交矩阵（(QQ^T=I)），(D=diag(lambda_1,lambda_2,...,lambda_n))。

[A=QDQ^T=(mathbf{q_1,q_2,...,q_n}) left{ egin{matrix} lambda_1 & & \ & lambda_2 & \ & & lambda_3 end{matrix} ight} left{ egin{matrix} q_1^T\ q_2^T\ ...\ q_n^T\ end{matrix} ight}\ =(lambda_1q_1,lambda_2q_2,...,lambda_nq_n) left{ egin{matrix} q_1^T\ q_2^T\ ...\ q_n^T\ end{matrix} ight}\ =sumlimits^{n}limits_{i=1}{lambda_iq_iq^T_i} ]

这里的({q_i}^n_{i=1})为(mathcal{R^n})空间中的一组正交基。

当一个矩阵可以进行特征值分解的时候，其特征向量构成了这个(n)维空间的一组基底.

2.核函数

每一个函数(f)都可以看做一个无限维的向量，那么二元函数(K(mathbf{x,y}))就可以看做是一个无限维的矩阵。如果它满足：

正定性

[intint f(x)K(mathbf{x,y})f(y)dxdy geqslant0 ]

对称性

[K(mathbf{x,y})= K(mathbf{y,x}) ]

那么它就是一个核函数。

3.Mercer定理

与矩阵特征值和特征向量类似，核函数存在特征值和特征函数（将函数看做无限维向量）。也就是：

[int K(mathbf{x,y})psi(mathbf{x})dx=lambdapsi(mathbf{y}) ]

类比于上面的矩阵，对于不同的特征值(lambda_1,lambda_2),及其对应的特征方程(psi_1(mathbf{x}),psi_2(mathbf{x}))

[int lambda_1 psi_1(mathbf{x})psi_2(mathbf{x})dx=int lambda_2 psi_2(mathbf{x})psi_1(mathbf{x})dx ]

因此，(<psi_1,psi_2>=intpsi_1(mathbf{x})psi_2(mathbf{x})dx=0).即特征方程是正交的。

一个核函数对应无穷个特征值({lambda_i}^{infty}_{i=1})和无穷个特征方程({psi_i}^{infty}_{i=1})。和矩阵类似，

[K(mathbf{x,y})=sumlimits^{infty}limits_{i=0}lambda_i psi_i(mathbf{x})psi_j(mathbf{y}) ]

这里(psi_i ,psi_j geqslant0,i eq j)。({psi_i}^{infty}_{i=1})是原来函数空间的一组正交基。

4.核函数的作用以及通俗理解

问题：给杜两个向量(mathbf{x_i,x_j})，目标是要计算它们的内积(I=<mathbf{x_i,x_j}>)。

现在通过某种非线性变换(Phi:mathbf{x ightarrow phi(x)})被它们映射到一个高维空间中，映射后的变量就变成了(phi(x_i),phi(x_j))，映射后的内积变为(I^{'}=<phi(x_i),phi(x_j)>)。

那么现在要如何计算变换后的内积呢？

传统方法是先计算映射后的向量(phi(x_i),phi(x_j))，然后再计算它俩的内积。但是这样做计算很复杂，因为映射到高维空间后的数据维度很高。比如，假设(mathbf{x_i,x_j})映射之后都是一个(1×10000)维的向量，那么他们的内积计算就需要做10000次加法操作和10000次乘法操作，显然复杂度很高。

那么能不能在原始空间找到一个函数(K(mathbf{x_i,x_j}))使得(K(mathbf{x_i,x_j})=<phi(x_i),phi(x_j)>)？如果可以的话，我们就可以在低维空间直接计算(K(mathbf{x_i,x_j}))的值，不需要先把数据映射到高维空间，再通过复杂的计算求解映射后的内积了。这样的函数是存在的，这样的函数叫做核函数。

例子： $$x = (x1, x2, x3, x4); y = (y1, y2, y3, y4)$$

[f(x) = (x1x1, x1x2, x1x3, x1x4, x2x1, x2x2, x2x3, x2x4, x3x1, x3x2, x3x3, x3x4, x4x1, x4x2, x4x3, x4x4) ]

(f(y))同理。令核函数(K(mathbf{x,y})=(<mathbf{x,y}>)^2).

[x = (1, 2, 3, 4); y = (5, 6, 7, 8). ]

不使用核函数：$$f(x) = ( 1, 2, 3, 4, 2, 4, 6, 8, 3, 6, 9, 12, 4, 8, 12, 16) ;$$

[f(y) = (25, 30, 35, 40, 30, 36, 42, 48, 35, 42, 49, 56, 40, 48, 56, 64) ; ]

[<f(x), f(y)> = 25+60+105+160+60+144+252+384+105+252+441+672+160+384+672+1024 = 4900.]

使用核函数：(K(mathbf{x,y})=(5+12+21+32)^2=70^2=4900)

再生核希尔伯特空间

将({sqrt{lambda_i}psi_i}^{infty}_{i=1})作为一组正交基构建一个希尔伯特空间(mathcal{H}),这个空间中的任何一个函数（向量）都可以表示为这组基的线性组合。如

[f=sumlimits^{infty}limits_{i=1}f_isqrt{lambda_i}psi_i ]

则(f)就可以表示为(mathcal{H})中的一个无限维的向量：(f=(f_1,f_2,...)^T_{mathcal{H}}),(K(mathbf{x,y}))表示二元函数或无限维矩阵，(K(mathbf{x,·}))就可以表示矩阵第x行的一元函数或无限维向量，也就是固定核函数的一个参数为x，那么

[K(mathbf{x,·})=(sqrt{lambda_1}psi_1(mathbf{x}),sqrt{lambda_2}psi_2(mathbf{x}),...)^T_{mathcal{H}} ]

同样的，

[K(mathbf{y,·})=(sqrt{lambda_1}psi_1(mathbf{y}),sqrt{lambda_2}psi_2(mathbf{y}),...)^T_{mathcal{H}} ]

因此，

[<K(mathbf{x,·}),K(mathbf{y,·})>_{mathcal{H}}=sumlimits^{infty}_{i=0}{lambda_i psi_i(mathbf{x})psi_i(mathbf{y})}=K(mathbf{x,y}) ]

以上就是核的可再生性(reproducing)，即用核函数来再生两个函数的内积。也被叫做可再生核希尔伯特空间.

具体定义

设(mathcal{H})是一个由定义在非空集合(mathcal{X})上的函数(f:mathcal{X} ightarrow mathbb{K})构成的希尔伯特函数空间，若函数(k：mathcal{X} imesmathcal{X} ightarrowmathbb{R})满足：

[∀x∈mathcal{X} ,k(⋅,x)∈mathbb{K} ]
[∀x∈mathcal{X},∀f∈mathcal{H},left <f,k(⋅,x) ight >_mathcal{H}=f(x) ]
[∀x,y∈mathcal{X},k(x,y)=left <k(⋅,x),k(⋅,y) ight >_mathcal{H} ]

其中(<⋅,⋅>_mathcal{H})是内积，则(k)称为(mathcal{H})的再生核函数，(mathcal{H})称为再生核希尔伯特空间（RKHS）.

距离⟶范数⟶内积

向量空间+范数⟶ 赋范空间+线性结构⟶线性赋范空间+内积运算⟶内积空间+完备性⟶希尔伯特空间

内积空间+有限维⟶欧几里德空间

赋范空间+完备性⟶巴拿赫空间

转载或参考：