什么是完全背包
完全背包,就是在背包容量有限的情况下,每件物品可以选无数多件。
如何求解完全背包
完全背包和01背包一样,拥有最优子结构。所以也可以用动态规划来解。
还是先确定动态转移方程,把01背包的转移方程进行发展,可以得到
K表示选k件n类物品。其实01背包也可以用这个递推式来解的,只是k非0即1。
优化动态转移矩阵
如何优化这个转移矩阵呢?我们先回顾一下01背包是怎么优化的?我们把二维矩阵优化成一维数组,但是在计算时m要逆序。为怎么呢?因为第n件物品是不能复选的。
那我们在来看看如果m不逆序会发生什么?
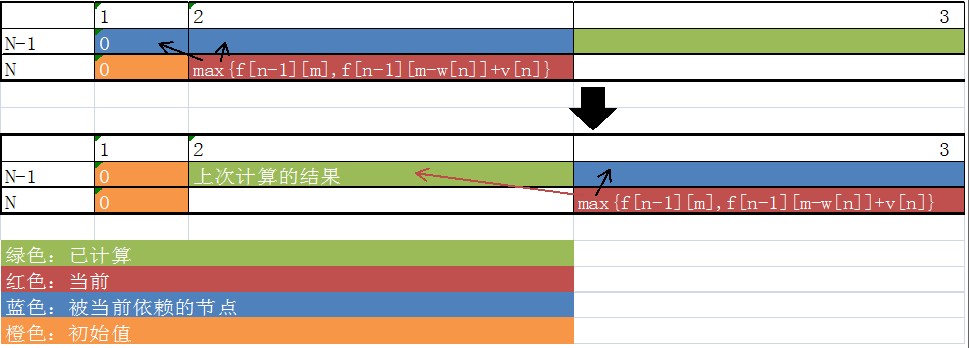
我们来看看“上次计算的结果”是什么呢?“上次计算的结果”无非是两种情况(f[n-2][m])或者是(f[n-2][m-w[n-1]]+v[n-1])
先考虑第二种情况叠加的情况,就会发现。。。我们根本没法叠加。但是如果我们把转移式改成
,就可以叠加了(就是后面那个n不减了)。结果发现这和
是等价的。那不就正好达到了取2件i物品的目的吗。在这样叠加上去,就和取k件i物品就等价了。这时候你可能会产生这样一个问题,如果像我这样选的话,那k就是有限大的,最大就是M(这是由M次的循环所导致的)。这不是有违完全背包的定义吗?不会的,因为就算物品是无限的,但是你的背包容量是有限的。最大不可能超过(Mdiv w[n])件。所以不可能出现问题。
再次强调m在这里要顺序,就像这样:
memset(f,0,sizeof f);
for (int n = 0; n < N; ++n) {
for (int m = 0; m < M; ++m) {
f[m] = max(f[m], f[m - w[n]] + v[n])
}
}
转化成01背包
上面的解释你可能根本没看懂。不要紧,你只要能理解01背包,完全背包就不是问题。因为完全背包可以转化为01背包!
我们在上面看到,虽然物品数量是有限的,但是由于背包容量有限,所以可选的物品也是有限的。选第n种物品的最大数量是(M/w[n])。那我们就可以把(M/w[n])件物品全部拆开,使用01背包的递推式求解。
但是上面的方法有一个缺陷,那就是如果M很大的话,dp的复杂度会大得惊人。于是我们需要一个更高效的转化方法。
当然,转化的总方针是不会变的,就是拆拆拆。把一中物品拆成多件物品。我们只是要找到一种更高效拆的方法。
这时候我们会想到二进制。我们可以把单件物品“打包”,打包成(2^k)件的“套装”。这样我们既可以保证完备性,又可以大大降低复杂度。核心代码如下
int n1 = 0;
while (s>=t) {
v[++n1]=x*t; //相当于n1++; v[n1]=x*t;
w[n1]=y*t;
s-=t;
t*=2;
}