前言:感觉有些地方挺有意思,写一篇博客记录一下。
---------------------
一些前提:
1.OI中的博弈游戏是平等组合游戏。
2.所有情况都包含在一个有限的状态集中。
3.所有情况组合能构成一张有向无环图,即游戏能在有限步内结束,不存在无解的情况。
4.所有的规定对于游戏双方都是相同的。
5.两个人都是绝顶聪明,都会按照最优策略走步。
性质:游戏里只有两种情况:必胜态和必败态。必胜态的后继一定是必败态,必败态的后继一定是必胜态。
简单模型:
1.巴什博弈
只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个,最后取光者得胜。问是否先手必胜。
显然$nleq m$时先手必胜,$n=m+1$时先手必败。
当$m+1leq nleq 2*(m+1)$时,先手总能找到一个操作使得局面变为$m+1$。
所以不管怎么操作,总有一种方案使得后手操作完后物品减少$m+1$。
根据数学归纳法,得到当$nmod (m+1)=0$时先手必败,其他情况先手必胜。
2.Ferguson博弈
进行游戏需要用到两个盒子,在游戏的开始,第一个盒子中有$n$枚石子,第二个盒子中有$m$个石子(n, m > 0)。参与游戏的两名玩家轮流执行这样的操作:清空一个盒子中的石子,然后从另一个盒子中拿若干石子到被清空的盒子中,使得最后两个盒子都不空。当两个盒子中都只有一枚石子时,游戏结束。最后成功执行操作的玩家获胜。问是否先手必胜。
结论:当$(x,y)$中有一个为偶数,那么先手必胜。如果都为奇数,那么先手必败。
显然$(1,1)$时先手必败。假设$max(x,y)<k$时结论都成立,现在证明$max(x,y)=k$时结论成立。
如果$(x,y)$中有一个偶数,那么先手可以将这个偶数拆分成两个奇数$(x',y')$。因为$max(x',y')<k$,结论成立,且两个都为奇数,所以先手必胜,后手必败。
如果$(x,y)$中两个都为奇数,那么先手只能将奇数拆分成一奇一偶。$max(x',y')<k$,这种情况对于后手来说必胜,所以先手必败。
3.威佐夫博弈
有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。问是否先手必胜。
手玩几组数据,我们发现这些情况都是必败的(默认$aleq b$):$(0,0),(1,2),(3,5),(4,7),(6,10)cdots$
发现一些有趣的性质:将所有情况放在平面直角坐标系上,发现每一行和每一列只有一个必败态。且对于所有的必败态都有$b_i-a_i=i$。

即如果$(a,b)$是必败态,那么$x=a,y=b,y-b=x-a$上的其他点都是必胜态。
我们简单证明一下:
定理$0$:$(a,b)$等价于$(b,a)$。所以后面的讲述我们默认$aleq b$。
定理$1$:若$(a,b)$必败,则$(a,b+k)$必胜。显然。
定理$2$:若$(a,b)$必败,那么$(a+d,b+d)$必胜。同定理$1$。
定理$3$:所有必败态中,每个数字仅出现一次。
若一个数字出现两次,不妨设为$(a,i),(a,j)$。两者间有转移关系,但根据博弈论性质可知不可能从必败态又转移到必败态。所以不成立。
若一个数字不会出现,不妨设这个数字为$A$。显然小于$A$的数字个数是有限的,所以它们产生的形如$y=b$和$y-b=x-a$的直线与$x=A$的交点是有限的,因此肯定会有一个必败态。
所以在所有必败态中每个数字出现且仅出现一次。
关于$frac{sqrt 5+1}{2}$的详细证明,笔者不太会,直接上图吧。



总结:如果$(n-m)*frac{sqrt 5+1}{2}=m$先手必败,其余情况先手必胜。
Nim游戏
有若干堆石子,两个人轮流从某一堆取任意多的石子,规定每次至少取一个,多者不限,最后取光者得胜。问是否先手必胜。
Bouton's Theorem:局面为先手必败当且仅当各堆石子数异或和为0。
证明:结束状态异或和为$0$。设当前异或和为$x$,$x$的二进制最高位为$k$,必然存在一堆石子$y$的二进制第$k$位为$1$。使$y$变成$y xor x$将异或和变为$0$。因此不管什么情况都有操作使得一个人无法摆脱必败状态。
阶梯Nim游戏:
有$n$个格子,每个格子上只能放一个石子。石子可以向左放到没有石子的格子上,但不能跨越某个已经有石子的格子。无法操作者输。问是否有先手必胜策略。
我们把两个石子间空着的格子数看为一堆石子,当距离缩小$j$就等于在这一堆石子拿走$j$个。所以现在题意转化为:有$n$堆石子,每次可以从第$i$堆的石子中拿走一部分放到第$i-1$堆中,或者把第$1$堆中的石子拿走一部分,无法操作者算输。问是否有先手必胜策略。
结论:把最后一堆看成奇数堆,只看奇数堆石子个数然后按照普通Nim游戏做就行了。
证明:因为不管奇数堆怎么移动,总会移动到偶数堆。而偶数堆可以进行模仿操作,将石子移动到下一奇数层。那么奇数层拿到偶数层的石子相当于丢掉了。
问:为什么不能考虑偶数堆?
画个图:
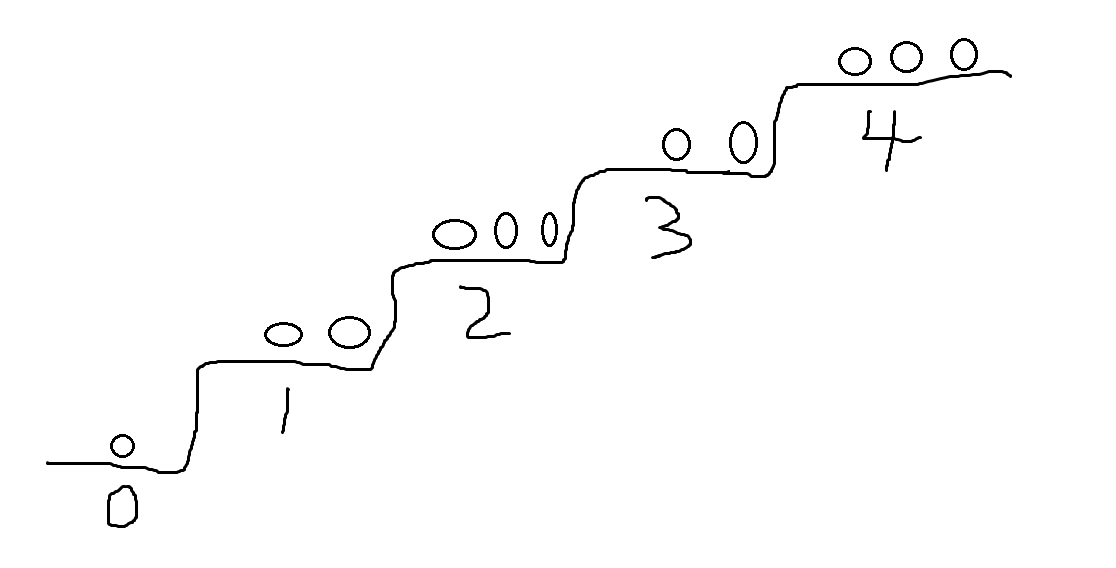
因为还有一个$0$号堆的存在……在原问题中场上的石子是不能拿走的。如果考虑偶数堆到最后偶数堆异或和永远不为$0$直接GG。
SG函数
首先定义$mex$运算:这是一个施加于集合的运算,表示最小的不属于这个集合的非负整数。例如$mex(0,1,2,3)=4,mex(0,2,5)=1$
组合有向图游戏:给定一个有向无环图和一个起始顶点上的一枚棋子,两名选手交替的将这枚棋子沿有向边进行移动,无法移动者判负。
对于一个给定的有向无环图,它的每个顶点SG函数为$sg(x)=mex(sg(y)|y=to(x))$
给一张图:
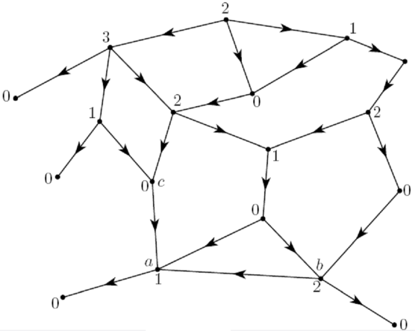
首先对于那些没有出边的结点它的$sg(x)=0$。
对于一个$sg(x)=0$的顶点,它的前驱的$sg$一定不为$0$;对于一个$sg$不为$0$的点,一定会有一个后继其$sg=0$。
因此我们可以得到:当$sg(x)=0$时先手必败,否则先手必胜。所以这种组合有向图游戏得到了解决。
组合有向图游戏和Nim游戏
如果sg函数的用途就这,那也太水了。现在将有向图游戏变得复杂一点:有向图上有$n$枚棋子在动。问必胜策略。
我们重新考虑$mex$运算:对于一个点$x$,它的sg函数值为$sg(x)$,那么遍历它的后继一定可以得到$0~sg(x)-1$的所有值且不可能得到$sg(x)$。
联想Nim游戏:现在某一堆石子有$k$个,你可以将它变为$0~k-1$,但不能保持$k$个。
是不是发现了什么?
也就是说,如果将n枚棋子所在的顶点的SG值看作$n$堆相应数量的石子,那么这个Nim游戏的每个必胜策略都对应于原来这$n$枚棋子的必胜策略!
所以组合有向图游戏和Nim游戏等价!
所以我们可以得到结论:当所有棋子所在顶点的SG函数值异或和为$0$,那么先手必败;否则先手必胜。
而获胜策略可以使用和Nim游戏一样的方法:如果对手改变局面使得异或和不为$0$,那么我们仍可以将异或和重新变回来,使对手永远无法摆脱必败态。
Sprague-Grundy Theorem
现在定义一个组合有向图游戏$G$,现在它有$n$个子游戏$G_1,G_2,cdots,G_n$。游戏$G$的移动规则是:任选一个子游戏$G_i$,并移动上面棋子。那么我们有:
$sg[G]=sg[G_1] xor sg[G_2] xor cdots xor sg[G_n]$
翻硬币游戏
一般的翻硬币游戏的规则是这样的:
1.$N$枚硬币排成一排,有的正面朝上,有的反面朝上。我们从左开始对硬币按$1$到$N$编号。
2.游戏者根据某些约束翻硬币(如:每次只能翻一或两枚,或者每次只能翻连续的几枚),但他所翻动的硬币中,最右边的必须是从正面翻到反面。
3.谁不能翻谁输。
定理:局面的SG值为局面中每个正面朝上的棋子单一存在时的SG值的异或和。
$sg[011001]=sg[01] xor sg[001] xor sg[000001]$
各种游戏规则的翻硬币游戏:
1.每次只能翻一个硬币
对于正面朝上的硬币,其SG值为$1$。如果有奇数个硬币朝上,则场上异或和为$1$,先手必胜;反之先手必败。
2.每次能翻一个或两个硬币(不用连续)
如果翻一个硬币,那么场上异或和为$0$;如果翻两个硬币,那么将有$sg[j](j<i)$。所以$sg[j]=mex(0,sg[j](j<i))$,即$sg[i]=i$。
3.每次只能翻$k$个连续的硬币
显然$n=0~k-1$时$sg[n]=0$,$n=k$时$sg[n]=1$。$n=k+1~2k-1$时$sg[n]=0$,$n=2k$时$sg[n]=1$cdots
根据数学归纳法可证当$n$为$k$的倍数时$sg[n]=1$,其余状态$sg[n]=0$。
4.每次可以选择翻动$1,2,3$个硬币
翻动一个时,后继$sg=0$;
翻动两个时,后继状态为$sg[j](j<i)$
翻动三个时,后继状态为$sg[j] xor sg[k]$
于是我们可以得到一个打表程序:
#include<bits/stdc++.h> using namespace std; int sg[1005],vis[1000005]; int main() { sg[1]=1;printf("%d ",sg[1]); for (int i=2;i<=1000;i++) { memset(vis,0,sizeof(vis)); vis[0]=1; for (int j=1;j<i;j++) vis[sg[j]]=1; for (int j=1;j<i;j++) for (int k=j+1;k<i;k++) vis[sg[j]^sg[k]]=1; for (int j=0;;j++) if (!vis[j]){sg[i]=j;break;} printf("%d ",sg[i]); } return 0; }
树形删边游戏
规则如下:给出一个有N个点的树,有一个点作为树的根节点。游戏者轮流从树中删去边,删去一条边后,不与根节点相连的部分将被移走。谁无边可删谁输。
定理:叶子节点的SG值为$0$;中间节点的SG值为它的所有子节点的SG值+1后的异或和。
证明没看太懂……挂到博客来吧
[证明](数学归纳法)
1.一个节点和两个节点的情况显然成立。
2.我们假设小于等于K个节点的任意情况均成立,下面证明(K+1)个节点的情况也成立。我们将证明分成两部分:(1)证明根节点只有一个孩子的情况符合要求;(2)证明根节点有多个孩子的情况符合要求。
Part1:
我们假设树$G$的根为$A$,$A$只与$B$相连,图中共有$N+1$个节点,去掉$A$后以$B$为根节点的图为$G’$ ,下面证明
当砍掉$A$与$B$相连的边时,sg为0,也就是说存在后继$0$
当砍掉$G'$中的一条边时,图中还剩$N$个点,设此时$G'$的sg值为$P$
那么此时$A$的sg为$P+1$,因为此时$A$中只有$N$个点,
而对于所有$N$个点的情况我们都有$G=G'+1$,所以$A$的后继局面有$P+1$
因为$G'$对应$0~sg[G']-1$都可以到达,也就是说$P$遍历$1~sg[G']$;
又存在后继局面$0$,所以$sg[G]=sg[G']+1$;
Part2:
对于$G'1,G'2…$它们各自对应的sg是$sg[G'1]+1$;
每棵子树互相独立!如果我们把每棵子树当做一堆石子,那么结论就可由Nim游戏规约得到!
证毕。
推荐题目
咕咕咕……