Treap=Tree+Heap,即在普通二叉查找树的基础上每个节点有了一个新值域:强化值(因为它将普通二叉查找树强化为treap就自己起了这个名字,是用来满足堆性质的,即后文说满足堆性质都指强化值满足堆性质)。要求这个树节点的键值(即要代表的数)满足BST的性质、强化值满足小跟堆的性质(你非得大根堆也没什么)。强化值由建立节点时由一个随机算法(rand())给出,在一个以随机数据建成的堆的加持下,treap的期望高度被证明为logn,故是一个平衡树。
代码请看文末
核心操作:旋转
左旋(zig):左旋一棵子树,它的根变为新子树的左儿子、根的右儿子变为新子树的根,那么根的右儿子的新左儿子是根了,原来的左儿子怎么办?交给根刚好。这样操作会发现,BST的性质仍然满足(相对左右位置未变),整个树宏观上向左“转动”了一下。
右旋(zig):右旋一棵子树,它的根变为新子树的右儿子、根的左儿子变为新子树的根,根的右儿子的原左儿子也可交给根。这样操作会发现,BST的性质仍然满足(相对左右位置未变),整个树宏观上向右“转动”了一下。
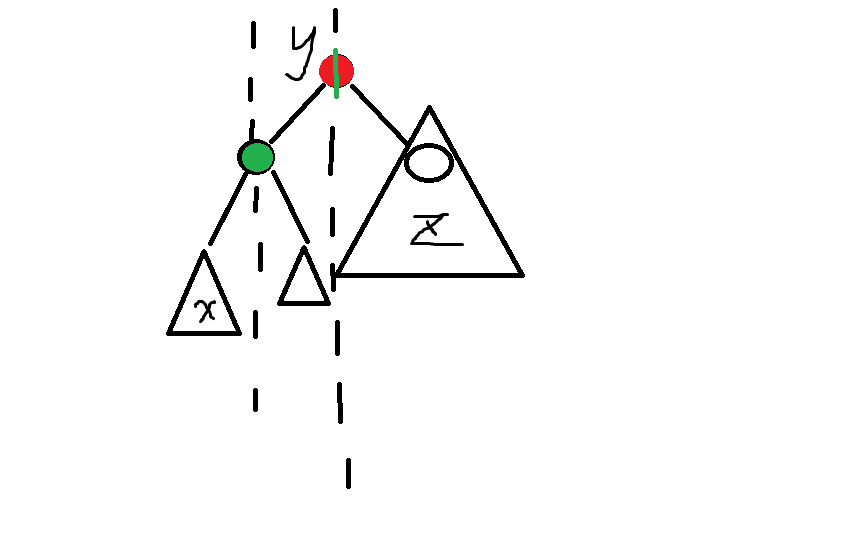
故:旋转不改变BST性质,但会改变父祖关系。同时不改变如图x、y、z三部分的堆性质(不特指某种旋转。红点为即将认父的根,绿点为即将认儿的子节点。x为会变为绿点的外侧子树,z代表原根的另一个子树,y代表内侧绿点会给红点的子树)
泛用操作:
1、插入x数:
按照普通二叉查找树插入方式新建节点后使其获得强化值。回溯过程中看儿子:左儿子强化值小于自己——右旋(让他当新爹,小根堆嘛);右儿子强化值小于自己——左旋。
解答为何用旋转方式维护堆性质:首先旋转不改变BST性质,但可以改变父子关系。看上图,若绿点强化值小于红点,有堆性质得,绿点要当红点父亲才行。一开始绿点子树一定是满足堆性质的(只有它一个点),因为绿点强化值小于红点,所以绿点完全可以当红点子树的根。由于红点子树在插入值前满足堆性质,而绿点一定是旋转上来的,所以红点可以当除绿点外子树所有点的父亲/祖先,故旋转完成后,红点为首的子树变为绿点为首的子树,同时整个子树都满足堆性质了。
2、删除x数:
思路类似普通二叉查找树,找到节点后,若cnt(为了考虑重复值而设的)>1,则cnt--,否则,若:
其最多只有一个子节点:让子节点代替他(若有的话),若没有,直接删就好。
有两个子节点:旋转,让强化值小的子节点当新爹,把原爹(即要删的)旋下去,直到删它的情况变为第一种。
解答这里为何旋转:强化值小的子节点可以当原子树内除原爹外所有点的父亲/祖先,旋转后子树不含原爹为首新子树的部分仍满足堆性质。以原爹为首的新子树除了原爹,强化值最小的(即原爹的原另一个强化值较大的子节点)点也没原爹现在的新爹(即原爹的原强化值较小的子节点)小,故可预知删除原爹后,整个树仍满足堆性质。
3、查询x数的排名 4、查询排名为x的数 5、求x的前驱 6、求x的后继 这些操作与二叉查找树的操作无异,见:二叉查找树
7、分离:
要把一个Treap按大小分成两个Treap,即大于等于x的分离成一个treap,剩下的也成一个treap,只要加一个虚拟节点(在需要分开的两点间,或某个叶子结点的儿子,看实际情况。怎么找?前驱或后继),然后将虚拟节点旋至根节点删除,左右两个子树就是得出的两个Treap了。根据二叉排序树的性质,这时左子树的所有节点都小于右子树的节点。时间相当于一次插入操作的复杂度,也就是 log( n )
8、合并:
合并是指把两个Treap合并成一个Treap,本文指其中第一个Treap的所有节点都必须小于或等于第二个Treap中的所有节点,先不涉及两个普通treap的合并。只要加一个虚拟的根,把两棵树分别作为左右子树,然后把根删除就可以了。时间复杂度和删除一样,也是期望O(log n)
练习题:

#include<iostream> #include<cstdio> #include<algorithm> //#include<cstdlib> using namespace std; const int N=100005; int n,root,bnt; struct node{ int ls,rs,cnt,siz,val,dev; }tre[N]; char ch; bool f; inline int read() { int x=0; f=0; ch=getchar(); while(!isdigit(ch)) f|=ch=='-',ch=getchar(); while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar(); return f?-x:x; } inline void upt(int u) { tre[u].siz=tre[tre[u].ls].siz+tre[tre[u].rs].siz+tre[u].cnt; } inline void zig(int &u) { int v=tre[u].rs; tre[u].rs=tre[v].ls; tre[v].siz=tre[u].siz; tre[v].ls=u; upt(u); u=v; } inline void zag(int &u) { int v=tre[u].ls; tre[u].ls=tre[v].rs; tre[v].siz=tre[u].siz; tre[v].rs=u; upt(u); u=v; } void insert(int &u,const int &val) { if(!u) { u=++bnt; tre[u].val=val; tre[u].cnt=tre[u].siz=1; tre[u].dev=rand(); return; } tre[u].siz++; if(tre[u].val==val) { tre[u].cnt++; return; } if(val<tre[u].val) { insert(tre[u].ls,val); if(tre[tre[u].ls].dev<tre[u].dev) zag(u); } else { insert(tre[u].rs,val); if(tre[tre[u].rs].dev<tre[u].dev) zig(u); } } void del(int &u,const int &val) { if(!u) return; if(tre[u].val==val) { if(tre[u].cnt>1) { tre[u].cnt--; tre[u].siz--; } else { if(tre[u].ls&&tre[u].rs) { if(tre[tre[u].ls].dev<=tre[tre[u].rs].dev) { zag(u); tre[u].siz--; del(tre[u].rs,val); } else { zig(u); tre[u].siz--; del(tre[u].ls,val); } } else if(tre[u].ls||tre[u].rs) u=tre[u].ls+tre[u].rs; else u=0; } return; } tre[u].siz--; if(val<tre[u].val) del(tre[u].ls,val); else del(tre[u].rs,val); } int finrank(const int &u,const int &val) { if(!u) return 1; if(tre[u].val==val) return tre[tre[u].ls].siz+1; if(val<tre[u].val) return finrank(tre[u].ls,val); else return finrank(tre[u].rs,val)+tre[tre[u].ls].siz+tre[u].cnt; } int finval(const int &u,const int &rnk) { if(rnk<=tre[tre[u].ls].siz) return finval(tre[u].ls,rnk); if(rnk>tre[tre[u].ls].siz+tre[u].cnt) return finval(tre[u].rs,rnk-tre[tre[u].ls].siz-tre[u].cnt); return tre[u].val; } int finpre(const int &u,const int &val) { if(!u) return -99999999; if(tre[u].val<val) { int k=finpre(tre[u].rs,val); return max(k,tre[u].val); } else return finpre(tre[u].ls,val); } int finnxt(const int &u,const int &val) { if(!u) return 99999999; if(tre[u].val>val) { int k=finnxt(tre[u].ls,val); return min(k,tre[u].val); } else return finnxt(tre[u].rs,val); } int main() { srand(9999); int n=read(); int opt,x; while(n--) { opt=read(),x=read(); switch(opt) { case 1: insert(root,x); break; case 2: del(root,x); break; case 3: printf("%d ",finrank(root,x)); break; case 4: printf("%d ",finval(root,x)); break; case 5: printf("%d ",finpre(root,x)); break; case 6: printf("%d ",finnxt(root,x)); break; } } return 0; }
结语:维持Treap的平衡性,强化值有着决定性的作用,故有时脸黑TLE也不是没有可能的。。。
补充:普通treap是不能O(log n)做区间操作的。为什么?因为你对al~ar没法快速标记。如确实想用treap做区间操作,移步fhq treap。因为fhq treap可将一个区间内的点全都裂成一个树,给这个树根打标记就完成了对整个区间的标记。
EX: 洛谷日报:不用旋转的treap?——fhq treap bug贼多不推荐了
参考资料:
