这题首先要切换角度,对着这个哈密顿回路瞪没啥用,我们考虑转化成每一个点的贡献。
我们任意挑选可行方案出来,发现每一个点 (u) (假设 (from) 连向它,它连向 (to))的贡献只有四种情况:
- (a_u<b_{to},b_u<a_{from}),这个点选取 (a_u) 和 (b_u) 都计入答案。
- (a_u<b_{to},b_u>a_{from}),这个点选取 (a_u) 都计入答案。
- (a_u>b_{to},b_u<a_{from}),这个点选取 (b_u) 都计入答案。
- (a_u>b_{to},b_u>a_{from}),这个点 (a_u) 和 (b_u) 都不计入答案。
同时满足:
- 选取的数((a) 被选的数量与 (b) 被选的数量之和)共计 (n) 个。
接下来我们从一个选取方案回推构图(哈密顿回路)方案。第一个想法是选取最小的 (n) 个数,但是这样是不对的,因为这样的选取方式不一定能对应一个方案。
我们看哈密顿回路中一条边的意义,为起点的 (a) 和终点的 (b) 选取较小的那个,这里我们可以采用一个技巧,把这个条件转化为起点的 (a) 和终点的 (b) 中选取且仅选取一个。
为什么这样正确?我们观察这样造成的多出来的一系列本应该不合法方案,发现如果这条边如果取另一个数答案一定更优,也就是说这些方案虽然不合法但是一定不能成为答案,所以,无所谓啦。
后面就简单了。
给出结论,只有这三种方案存在对应方案:
- 全选 (a)
- 全选 (b)
- 至少存在一个点 (a) 和 (b) 都被选择
前两种显然,不证了。
第三种口胡一下。
我们把左边那列视为 (a),右边那列视为 (b),选取的数为正方形,未选取的数为圆形。
我们要连 (n) 条边,连成一个环,一条边必须连接一个取和一个不取。
如果一部分选 (a),一部分选 (b),那么任意一个选 (a) 的点和任意一个选 (b) 的点是连不起来的,这个图不可能连通,所以不行。
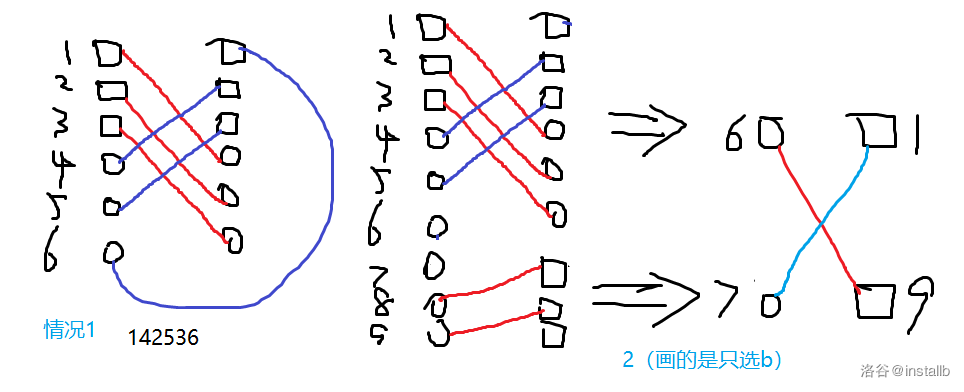
如果有 (k) 个都选,必然也有 (k) 个都不选,这里再分四种情况:
-
全是都选或都不选
-
都选 + 只选 (a)
-
都选 + 只选 (b)
和上一种本质一样。
-
都选 + 只选 (a) + 只选 (b)
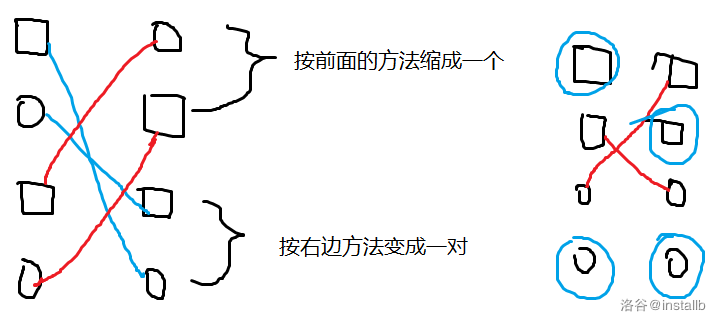
具体做法嘛。。前两个特判,后一种枚举一个强制两个都选,剩下所有数中的贪心选取最小的 (n-2) 个,因为其它点的选择是无所谓的。
这里先最小的 (n) 个全扔小根堆里,然后看每一个点强制双选的时候,它的 (a) 和 (b) 有几个数是在小根堆里,记为 (k),(k) 只能是 (0) 或 (1) 或 (2),用 (a) 和 (b) 中不在小根堆里的数之和加上小根堆中最小的 (n-k) 个数之和(这个可以预处理)更新答案。