updated Nov.29.2019
CSPS2019D2T2打卡(不过那道题比这道复杂多了 只是撞思路了?)
思路很妙的一道题
是道贪心 好像没人写证明 给个简单的证明吧
给出贪心结论 存在使得第一层最小的合法划分方式 使得层数最多(即得到最优解)
即一定能构造出一种最优解是满足这个解是第一段最小的
画个图:
假定方案2比方案1多分一段且两种方案均合法 并且方案2的第一段更长
我们假设方案2就是段数最多的一种方案
则一定能构造出一种分段数和2一样多的方案使得第一段和方案1一样大
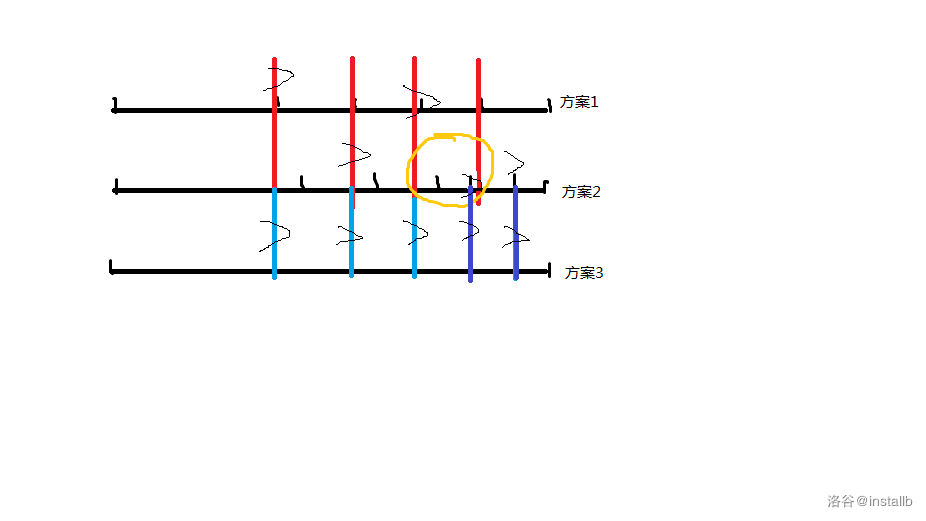
根据抽屉原理 黄圈中的部分一定会存在 即一定能构造出方案3 使得方案3合法 分段数与方案2相同 且第一段长度与方案1相等
只要存在分段数为小于最优解的分段方案 我们在确定第一段不变的情况下一定能够构造出分段数等于最优解的分段方案
具体实现
首先第一段要尽量小 这里我们先枚举第一段([1,i])的右端点(i) 由于所有数都是正数 所以(i)一定是越小越好的 这样才能使得第一段更小
此外 当(i)过小的时候 由于第二段、第三段...都是需要小于等于第一段的 可能会导致后面的段分不出来 所以我们需要寻找符合要求的最小的(i)
这个很难判断 但是当我们枚举(i)的时候 可以假装第一段已经确定 然后计算出([i+1,n])所有划分方案中第一段(从i+1开始的段)最小的方案 的 第一段的值
由于存在使得第一层最小的合法划分方式 使得层数最多 所以这在层数上也一定可以是最优解之一 并且对前面的限制更小
这样我们把问题转化为了子问题 即求出对于所有(i) 将([i,n])分段第一段最小值
后面就好办了 直接用一个看起来像DP的枚举就可以了
注意j越小越好 所以找到第一个符合要求的j就直接 确定答案+break
这里(d_i)记录了每一段分段的大小
for(int i = 1;i <= n;i ++) cin >> a[i];
for(int i = n;i >= 1;i --) s[i] = s[i + 1] + a[i];
for(int i = n;i >= 1;i --){
for(int j = i;j <= n;j ++){
if(s[i] - s[j + 1] < d[j + 1]) continue; // 不能划分
d[i] = s[i] - s[j + 1]; dp[i] = dp[j + 1] + 1;
break;
}
}
cout << dp[1] << endl;
这样是平方算法 我们需要快速确定j 减少无用的枚举
由于(s_i)和(d_j)是单调的 故(s_i+d_i)是单调的 满分算法需要要用单调队列优化
for(int i = 1;i <= n;i ++) cin >> a[i];
for(int i = n;i >= 1;i --) s[i] = s[i + 1] + a[i];
q[++ t] = 0;
for(int i = n;i >= 1;i --){
while(h < t && s[q[h + 1]] + d[q[h + 1]] <= s[i]) h ++;
d[i] = s[i] - s[q[h]]; dp[i] = dp[q[h]] + 1;
while(h <= t && s[i] + d[i] <= s[q[t]] + d[q[t]]) t --;
q[++ t] = i;
}