一、理论
递归问题 -> 重叠子问题、最优子结构 -> 记忆化搜索(自顶向下) -> 动态规划(记忆化 + 自底向上)
动态规划(Dynamic Programming),即动态递推(递归 + 记忆化 -> 递推)。动态规划问题的一般形式就是求最值。
1. 状态的定义:opt[n],dp[n],fib[n]
2. 状态转移方程:opt[n] = best_of(opt[n-1], opt[n-2], ...)
3. 存在重叠子问题,具备最优子结构. (最优子结构是指通过求子问题的最优解,可以获得原问题的最优解)
4. 自底向上。(这也是为什么动态规划不用递归,而是要循环迭代完成计算)
5. 状态压缩(滚动数组)。如果发现每次状态转移只需要DP数组的一部分,那么可以运用【滚动数组】的思想,进行状态压缩,只记录必要的数据,优化空间。
题目特点:动态规划的题目分为两大类,
一种是求最优解类,典型问题是背包问题。 当前问题的最优解取决于子问题的最优解。
另一种是计数类,如统计方案数等问题。 当前问题的方案数取决于子问题的方案数。
动态规划的解题步骤:
- 定义子问题
- 写出子问题的递推关系
- 确定 DP 数组的计算顺序
- 空间优化(可选)
DP vs 回溯 vs 贪心
回溯(递归)—重复计算
贪心—永远局部最优
DP—记录局部最优子结构 / 多种记录值
Note:何时用【回溯】,何时用【动态规划】? —— 如果是求走迷宫的【路径】,必然是回溯; 如果是走迷宫的【路径的条数 / 方案数】,必然是dp。
二、从斐波那契数谈起
经典的斐波那契数列的递归解法如下所示(时间复杂度为:O(2^n),为指数级复杂度),它的缺点在于有大量的子问题被重复计算。
class Solution { public int fib(int n) { // 执行耗时:10 ms,击败了17.41% 的Java用户 if (n == 0) return 0; if (n == 1) return 1; return fib(n - 1) + fib(n - 2); } }
优化方案1:记忆化搜索,自顶向下。 (时间复杂度:O(n),仍然需要递归)
class Solution { // 假设 memo[]数组已赋好初值,初始化都为-1 public int fib(int n) { if (n == 0) return 0; if (n == 1) return 1; if (memo[n] == -1) { // 如果没计算过 memo[n] = fib(n-1) + fib(n-2); } return memo[n]; } }
优化方案2:动态规划----记忆化自底向上。 (时间复杂度为O(n))
class Solution { public int fib(int n) { // 执行耗时:0 ms,击败了100.00% 的Java用户 // 内存消耗:35.3 MB,击败了40.50% 的Java用户 if (n == 0 || n == 1) return n; int[] arr = new int[n + 1]; arr[0] = 0; arr[1] = 1; for (int i = 2; i <= n; i++) { arr[i] = arr[i-1] + arr[i-2]; } return arr[n]; } }
优化方案3:空间优化 (当前状态只和之前两个状态有关,所以只存储之前两个状态即可,空间复杂度可降为O(1))
class Solution { public int fib(int n) { // 执行耗时:0 ms,击败了100.00% 的Java用户 // 内存消耗:35.1 MB,击败了79.25% 的Java用户 /* if (n == 0 || n == 1) return n; int n1 = 1; // 第n-1项 int n2 = 0; // 第n-2项 int sum = 0; for (int i = 2; i <= n; i++) { sum = n1 + n2; n2 = n1; n1 = sum; } return sum; */ // 进一步优化 if (n == 0 || n == 1) return n; int sum = 1; // 利用 sum 存储第 n-1 项 int n2 = 0; for (int i = 2; i <= n; i++) { sum = sum + n2; n2 = sum - n2; } return sum; } }
三、0-1背包问题(参考资料:bobo、背包九讲)
问题描述:背包的容量为C,有n中不同的物品,编号为0...n-1,每一件物品的重量为w(i),价值为v(i)。问可以向背包中放哪些物品,使得在不超过背包容量的基础上,物品的总价值最大。
问题初探:该问题不能使用贪心算法(优先放入平均价值最高的物品),举例可发现行不通。
问题分析:设F(n,c)为考虑将n个物品放在容量为c的背包中,使得价值最大。每一个物品都有 放 与 不放,两种状态。
F(i,c) = max( F(i-1,c) , v(i) + F( i-1, c - w(i)) )
重叠子问题在:同样的 i 和 c数据对,可能计算了多次。

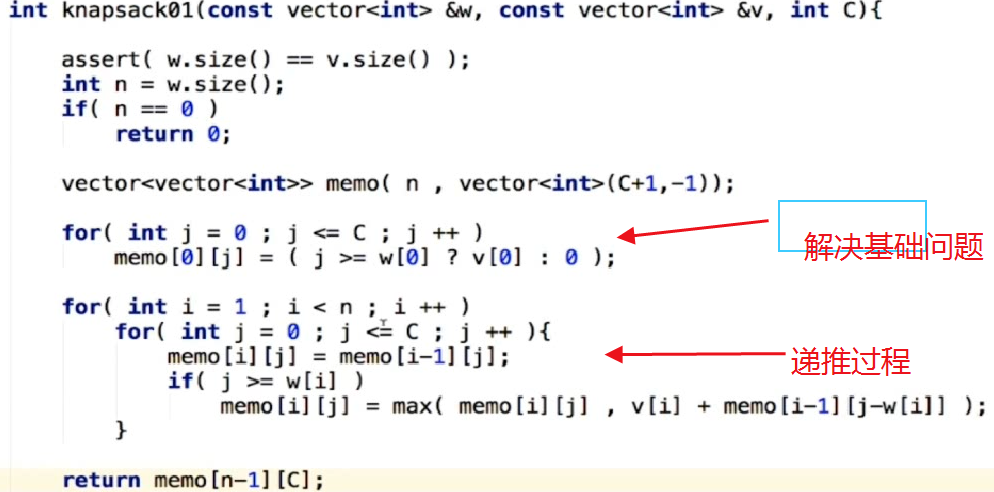
0-1背包问题的复杂度分析: 时间复杂度O(n*C) 空间复杂度O(n*C)
0-1问题的优化1(滚动数组):由状态转移方程可以看出,第 i 行元素只依赖于第i-1行元素。理论上,只需要保持两行元素,空间复杂度可以优化为O(2*C) = O(C)。 具体实现上,可以根据 i 的奇偶性,轮流使用两行数组。
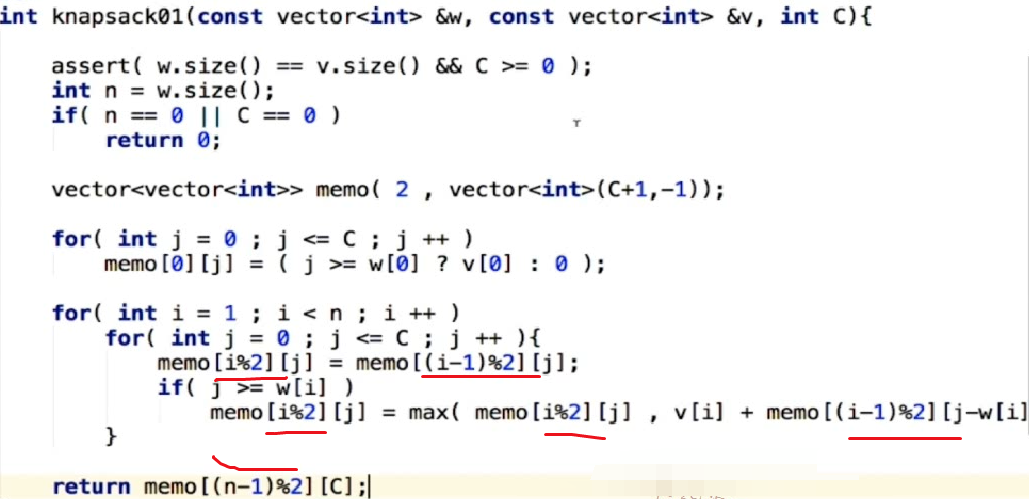
0-1问题的优化2(只使用一维数组):由于第二行当前格子的计算依赖于前一行上边 和 左边 某个格子的信息,而不会碰右边的格子。因此,只有一行时,可以从右向左进行计算。
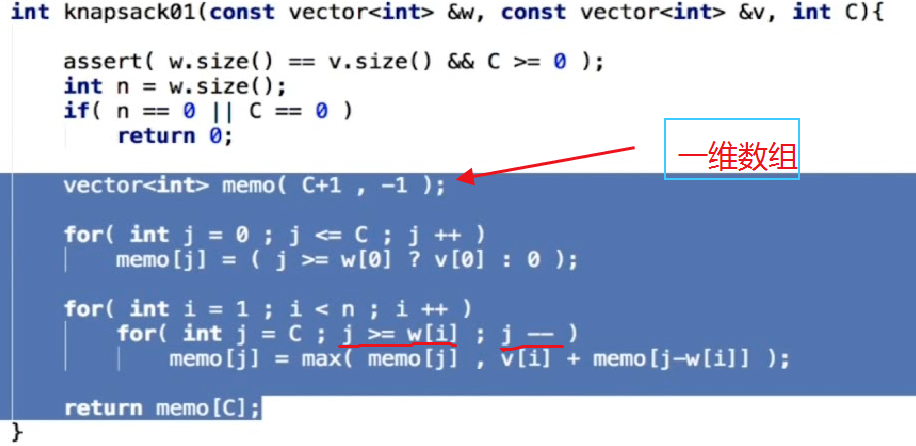
0-1背包问题的变种
(1)完全背包问题:每个物品可以无限使用。
分析:由于背包容量是有限的,那么每个物品可以取到的个数有最大值,因此,可以转化为普通背包问题,区别在于物品选取列表中,很多物品是重复的。更进一步,可以用二进制优化重复物品的个数,如1,2,4,8,16...。
(2)多重背包问题:每个物品不止1个,有num(i)个。
(3)多维费用背包问题:要考虑物品的体积和重量两个维度?
分析:状态需要多一个参数,设置三维数组
(4)物品间约束,如物品间相互依赖或相互排斥。
背包问题题型归纳与技巧:希望用一种规律搞定背包问题
四、典型例题
①:爬楼梯问题(LC70、剑指08.跳台阶)
思路:本题是斐波那契数列的应用。
class Solution { public int climbStairs(int n) { /*if (n <= 2) return n; int n1 = 1; int n2 = 2; for (int i = 3; i <= n; i++) { n2 = n2 + n1; n1 = n2 - n1; } return n2;*/ // 写成动态规划的递推形式 if (n <= 2) return n; int[] dp = new int[n + 1]; dp[1] = 1; dp[2] = 2; for (int i = 3; i <= n; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[n]; } }
☆☆☆②:三角形的最小路径和(LC120、数字三角形问题(动态规划))
思路:本题是DP的经典题目。需要自底向上开始递推,首先定义DP的状态,然后推出DP方程。
优化:使用一维数组而不是二维数组,这样只使用了O(n)的额外空间。
class Solution { public int minimumTotal(List<List<Integer>> triangle) { // 方法1: 时间复杂度和空间复杂度 都是O(n^2) /*int n = triangle.size(); // 1. 状态的定义:dp[i][j]表示从点(i,j)到底边的最小路径和 int[][] dp = new int[n + 1][n + 1]; // 从三角形的最后一行开始递推。 for (int i = n - 1; i >= 0; i--) { for (int j = 0; j <= i; j++) { // 2. 状态转移方程 dp[i][j] = Math.min(dp[i + 1][j],dp[i + 1][j + 1]) + triangle.get(i).get(j); } } return dp[0][0];*/ // 由于递推中,计算dp[i][j]时,只用到了下一行的dp[i+1][j]和dp[i+1][j+1]。 // 而不需要记录整个层的结果,因此dp数组不需要定义N行,只需要一行即可。 // 方法2:进行空间优化,仅使用一维数组. 时间复杂度O(n^2),空间复杂度O(n) int n = triangle.size(); int[] dp = new int[n + 1]; for (int i = n - 1; i >= 0; i--) { for (int j = 0; j <= i; j++) { dp[j] = Math.min(dp[j],dp[j + 1]) + triangle.get(i).get(j); } } return dp[0]; } }
☆☆☆③:乘积最大子数组(LC152、剑指30.连续子数组的最大和)
思路:DP。关键点在于:由于存在负数,那么会导致最大的变最小的,最小的变最大的。因此还需要维护当前最小值imin。
视频:覃超P47
class Solution { public int maxProduct(int[] nums) { int max = Integer.MIN_VALUE; int imax = 1, imin = 1; for (int i = 0; i < nums.length; i++) { // 由于存在负数,那么会导致最大的变最小的,最小的变最大的。 // 当负数出现时则imax与imin进行交换再进行下一步计算 if (nums[i] < 0){ int temp = imax; imax = imin; imin = temp; } imax = Math.max(imax * nums[i], nums[i]); imin = Math.min(imin * nums[i], nums[i]); max = Math.max(max,imax); } return max; } }
☆☆☆☆☆☆④:动态规划解决买卖股票问题(LC121、LC122【40讲系列7】贪心 、LC123、LC188、LC309、LC714)
题目描述:
- LC121:一次买卖一支股票 (暴力解法、动态规划)
- LC122:多次买卖一支股票 (暴力解法、贪心算法、动态规划)
- LC123:最多两次买卖一支股票 (动态规划)
- LC188:最多K次买卖一支股票 (动态规划)
- LC309:多次买卖一支股票,并且卖出股票后无法在第二天买入股票(冷冻期1天) (动态规划)
- LC714:多次买卖但需要付手续费 (动态规划)
分析:前四个属于一类问题,LC121相当于K=1的情况;LC122相当于K为无穷的情况;LC123相当于K=2的情况;LC188属于一般情况(三维动态规划)
参考:
class Solution121 { public int maxProfit(int[] prices) { // DP写法1:前i天的最大收益 = max{前i-1天的最大收益,第i天的价格-前i-1天中的最小价格} if (prices == null || prices.length == 0) return 0; int min = prices[0]; int profit = 0; for (int i = 1; i < prices.length; i++) { profit = Math.max(profit, prices[i] - min); min = Math.min(min, prices[i]); } return profit; // DP此类问题的通用写法: /*if (prices == null || prices.length == 0) return 0; int len = prices.length; int[][] dp = new int[len][2]; dp[0][0] = 0; dp[0][1] = -prices[0]; for (int i = 1; i < len; i++) { dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]); dp[i][1] = Math.max(dp[i-1][1],-prices[i]);// 注意与122题对比,只允许交易一次,因此手上的现金数就是当天的股价的相反数 } return dp[len-1][0];*/ // 对上述代码进行空间优化 /*if (prices == null || prices.length == 0) return 0; int dp0 = 0, dp1 = -prices[0]; for (int i = 1; i < prices.length; i++) { dp0 = Math.max(dp0,dp1+prices[i]); dp1 = Math.max(dp1,-prices[i]); } return dp0;*/ } }
class Solution122 { public int maxProfit(int[] prices) { /** * 方法1:贪心(针对此问题的特殊解法,因为一天可以买卖无数次) * 当天卖出后,当天还可以买入。只要今天比昨天大,就卖出 */ int res = 0; for (int i = 1; i < prices.length; i++) { if (prices[i] > prices[i - 1]){ res += prices[i] - prices[i-1]; } } return res; /** * 方法2.1 : 动态规划 * 不能同时参与多笔交易,所以每天交易结束后只有持有一支股票和没有持有两种状态。 * dp[i][0]表示第i天交易完成后没有持股的最大利润 * dp[i][1] 表示第i天交易完成后持股的最大利润. * 第一种dp[i][0],说明第i天没有持股,此时有两种可能,前一天没有持股,今天也不买。或者前一天持股,在今天卖出。 * 第二种dp[i][1],说明第i天持有股票,此时有两种可能,前一天持股,今天保持不动。或者前一天没有持股,今天买入。 */ // int len = prices.length; // int[][] dp = new int[len][2]; // dp[0][0] = 0; // dp[0][1] = -prices[0]; // for (int i = 1; i < len; i++) { // dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]); // dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); // } // return dp[len - 1][0]; /** * 方法2.2:动态规划 * 由于今天的利润只和前一天相关,我们只需要记录前一天的利润。因此可以进行空间优化。 */ // int len = prices.length; // int dp0 = 0, dp1 = -prices[0]; // for (int i = 1; i < len; i++) { // int newDp0 = Math.max(dp0,dp1 + prices[i]); // int newDp1 = Math.max(dp1,dp0 - prices[i]); // dp0 = newDp0; // dp1 = newDp1; // } // return dp0; } }
class Solution123 { public int maxProfit(int[] prices) { /** * 针对此类问题的通用写法: * 注: 规定一次交易产生是在 【买入股票】 的时候,即买入股票时交易次数加1 */ /*if (prices == null || prices.length == 0) return 0; int len = prices.length; // 第 2 维的 0 没有意义,1 表示交易进行了 1 次,2 表示交易进行了 2 次 int[][][] dp = new int[len][3][2]; dp[0][1][1] = -prices[0]; dp[0][2][1] = Integer.MIN_VALUE; //注意不能初始化为0 for (int i = 1; i < len; i++) { // 转移顺序先持股,再卖出 dp[i][1][1] = Math.max(dp[i-1][1][1], -prices[i]); dp[i][1][0] = Math.max(dp[i-1][1][0], dp[i-1][1][1] + prices[i]); dp[i][2][1] = Math.max(dp[i-1][2][1], dp[i-1][1][0] - prices[i]); dp[i][2][0] = Math.max(dp[i-1][2][0], dp[i-1][2][1] + prices[i]); } return Math.max(dp[len-1][1][0],dp[len-1][2][0]);*/ /** * 对上述代码进行空间优化 * 由于今天只参考了昨天的状态,所以直接去掉第一维不会影响状态转移的正确性 */ /*if (prices == null || prices.length == 0) return 0; int[][] dp = new int[3][2]; dp[1][1] = -prices[0]; dp[2][1] = Integer.MIN_VALUE; for (int i = 1; i < prices.length; i++) { dp[1][1] = Math.max(dp[1][1], -prices[i]); dp[1][0] = Math.max(dp[1][0], dp[1][1] + prices[i]); dp[2][1] = Math.max(dp[2][1], dp[1][0] - prices[i]); dp[2][0] = Math.max(dp[2][0], dp[2][1] + prices[i]); } return dp[2][0];*/ // 收益值(dp[2][0] >= dp[1][0]) /** * 针对本题的变量写法: * buy1:第一次买入股票可获得的最大收益 * sell1:第一次卖出股票可获得的最大收益 */ if (prices == null || prices.length == 0) return 0; int buy1 = -prices[0], buy2 = Integer.MIN_VALUE; int sell1 = 0, sell2 = 0; for (int i = 1; i < prices.length; i++) { buy1 = Math.max(buy1, -prices[i]); sell1 = Math.max(sell1, buy1 + prices[i]); buy2 = Math.max(buy2, sell1 - prices[i]); sell2 = Math.max(sell2, buy2 + prices[i]); } return sell2; } }
class Solution188 { public int maxProfit(int k, int[] prices) { /** * 最一般的情况,相当于122题(K为无穷) 和 123题(K=2) 的融合。 * 如果k超过一个临界值,最大收益就不再取决于最大交易次数,而是取决于数组的长度 * 一个有收益的交易至少需要两天(在前一天买入,在后一天卖出,前提是买入价格低于卖出价格)。 * 如果数组长度为 n,则有收益的交易的数量最多为 n/2 ,因此如果k>=n/2,等价于k为无穷的情况。 */ if (prices == null || prices.length == 0) return 0; int len = prices.length; if (k >= len/2){ return greedy(prices); } int[][] dp = new int[k+1][2]; for (int kk = 1; kk <= k; kk++) { dp[kk][1] = -prices[0]; } for (int i = 1; i < len; i++) { for (int kk = 1; kk <= k; kk++) { dp[kk][1] = Math.max(dp[kk][1], dp[kk-1][0] - prices[i]); dp[kk][0] = Math.max(dp[kk][0], dp[kk][1] + prices[i]); } } return dp[k][0]; } // 相当于k为无穷的情况,LeetCode 122 public int greedy(int[] prices) { int res = 0; for (int i = 1; i < prices.length; i++) { if (prices[i] - prices[i-1] > 0){ res += prices[i] - prices[i-1]; } } return res; // 使用DP /*int[][] dp = new int[prices.length][2]; dp[0][1] = -prices[0]; for (int i = 1; i < prices.length; i++) { dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]); dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); } return dp[prices.length - 1][0];*/ } }
class Solution309 { public int maxProfit(int[] prices) { if (prices == null || prices.length == 0) return 0; int len = prices.length; // 定义三个状态: 注意定义的状态是第i天结束后的状态 // 1:持股; 0:不持股且不是冷冻期; 2:冷冻期(今天卖出,不持股) int[][] dp = new int[len][3]; dp[0][1] = -prices[0]; for (int i = 1; i < len; i++) { dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]); dp[i][2] = dp[i-1][1] + prices[i]; dp[i][0] = Math.max(dp[i-1][0], dp[i-1][2]); } return Math.max(dp[len-1][0], dp[len-1][2]); // 空间优化 /*int dp1 = -prices[0]; int dp0 = 0, dp2 = 0; for (int i = 1; i < len; i++) { int newDp1 = Math.max(dp1, dp0 - prices[i]); int newDp2 = dp1 + prices[i]; int newDp0 = Math.max(dp0, dp2); dp0 = newDp0; dp1 = newDp1; dp2 = newDp2; } return Math.max(dp0,dp2);*/ } }
class Solution714 { public int maxProfit(int[] prices, int fee) { // 与122题类似,只是多了手续费 if (prices == null || prices.length == 0) return 0; int len = prices.length; int[][] dp = new int[len][2]; dp[0][1] = -prices[0] - fee; for (int i = 1; i < len; i++) { dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]); dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i] - fee); } return dp[len-1][0]; /*int dp0 = 0, dp1 = -prices[0] - fee; for (int i = 1; i < len; i++) { int newDp0 = Math.max(dp0, dp1 + prices[i]); int newDp1 = Math.max(dp1, dp0 - prices[i] - fee); dp0 = newDp0; dp1 = newDp1; } return dp0;*/ } }
☆☆☆☆☆⑤:最长上升子序列(LC300)
Note:该题为不连续的情况,可以延伸到最长连续子序列长度该怎么求。 另外,除了要会求子序列的长度,还要会求出最长的子序列是什么。
方法1:DP----O(n^2)
方法2:二分-------O(nlogn)。 不是很理解二分的过程 T_T
class Solution { public int lengthOfLIS(int[] nums) { if (nums == null || nums.length == 0) return 0; /** * 方法1:动态规划,时间复杂度O(n^2) */ // 1.状态定义: dp[i]状态表示从开始到第i个元素结尾(包含第i个元素),最长子序列的长度 // 2.DP方程: dp[i] = max{dp[j] + 1} ( j<i, nums[j]<nums[i] ) /*int[] dp = new int[nums.length]; int res = 1; for (int i = 0; i < nums.length; i++) { dp[i] = 1; // 初始化。如果0到i-1中所有的数都不比第i个数小,则单独一个数是子序列 for (int j = 0; j < i; j++) { if (nums[j] < nums[i]){ // 以哪个数结尾的最大递增子序列更大,就选其作为倒数第二个数 dp[i] = Math.max(dp[i], dp[j] + 1); } } res = Math.max(res, dp[i]); // 所有dp[i]中找最大的 } return res;*/ /** * 方法2:二分查找,时间复杂度O(nlogn) * a.直接维护最长子序列数组res[],注意该数组是有序的 * 1)如果当前元素比结果数组的值都大,就追加在结果数组的尾部(相当于递增序列长度加1) * 2)否则,用当前元素覆盖掉第一个比它大的元素(比它大的元素中最小的那个)。 这样就能给后面数机会 * b.返回数组的长度 * 说明:由于每个数O(n)找到其要插入的位置用的是二分查找O(logn),所以总体是O(nlogn)的。 * 2)中的覆盖操作可能会导致最终的结果数组并不是最终的递增序列,但对长度无影响。 * 举个例子:[10,11,12,13,1,2,3,4,5] * ->[10,11,12,13]->[1,11,12,13]->[1,2,12,13] ....-> [1,2,3,4,5] */ int[] res = new int[nums.length]; int len = 0; // res当前的长度 for (int num : nums){ int start = 0, end = len; // 利用二分查找res数组索引为[0, len)之间元素,找到第一个大于num的元素。 while (start < end){ int mid = start + ((end - start) >> 1); if (res[mid] < num){ start = mid + 1; }else { end = mid; } } res[start] = num; if (start == len){ // 说明区间中不存在比num大的数+ len++; } // 调二分API /*int idx = Arrays.binarySearch(res,0,len,num); idx = idx < 0 ? -idx - 1 : idx; res[idx] = num; if (idx == len) len++;*/ } return len; } }
【拓展】:如何根据dp数组得到最长递增子序列是什么?------>参考左神P203
public int[] generateLIS(int[] arr, int[] dp) { int len = 0; int index = 0; for (int i = 0; i < dp.length; i++) { if (dp[i] > len){ len = dp[i]; index = i; } } int[] lis = new int[len]; lis[--len] = arr[index]; for (int i = index; i >= 0; i--) { if (arr[i] < arr[index] && dp[i] == dp[index] - 1) { lis[--len] = arr[i]; index = i; } } return lis; }
☆☆☆⑥:零钱兑换(LC322)
思路:转换成 “跳台阶” 问题。
class Solution { /** * 思路; 转化为跳台阶问题 * 1. 状态的定义: dp[i] 表示到i台阶时的最小步数, 也即凑齐i需要的最少硬币数 * 2. 状态转移方程 dp[i] = min {dp[i-coins[j]} + 1 * 举例: [1,2,5] 11 * dp[i] = min{i-1, i-2, i-5} + 1 * dp[11] = min{dp[10],dp[9],dp[6]} + 1 */ public int coinChange(int[] coins, int amount) { int[] dp = new int[amount + 1]; // 最多的硬币数就是全部使用面值1的硬币来换, amount+1是不可能达到的换取数量。 // 因为硬币面额最小为整数1,所以只要有解,最小硬币数必然小于amount+1 int max = amount + 1; Arrays.fill(dp, max); dp[0] = 0; for (int i = 1; i <= amount; i++) { for (int j = 0; j < coins.length; j++) { if (i >= coins[j]) { dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1); } } } return dp[amount] == amount + 1 ? -1 : dp[amount]; } }
☆☆☆⑦:计算最短编辑距离问题(LC72)
class Solution { /** * 1. 状态的定义:dp[i][j]:word1前i个字符 变为 word2前j个字符 所需最小操作数 * 最后返回dp[word1.length][word2.length] * 2. DP方程: 分两种情况, * 1)如果当前字母相同,则dp[i][j] = dp[i-1][j-1] * 2) 否则,取 删-增-替 的最小值 + 1, * 即 min{dp[i-1][j],dp[i][j-1],dp[i-1][j-1]} + 1 */ public int minDistance(String word1, String word2) { int len1 = word1.length(), len2 = word2.length(); int[][] dp = new int[len1 + 1][len2 + 1]; for (int i = 0; i <= len1; i++) { dp[i][0] = i; } for (int j = 0; j <= len2; j++) { dp[0][j] = j; } for (int i = 1; i <= len1; i++) { for (int j = 1; j <= len2; j++) { // 注意dp数组有一个偏移,所以是 charAt(i-1)而不是i if (word1.charAt(i-1) == word2.charAt(j-1)) { dp[i][j] = dp[i-1][j-1]; }else { // 分别对应 增,删,替 dp[i][j] = Math.min(dp[i][j-1],Math.min(dp[i-1][j],dp[i-1][j-1])) + 1; } } } return dp[len1][len2]; } }
五、扩展例题
第一组:LeetCode120. 三角形最小路径和、LeetCode64. 最小路径和
第二组(发现重叠子问题):LeetCode343. 整数拆分、LeetCode279. 完全平方数、LeetCode91. 解码方法、LeetCode62. 不同路径、LeetCode63. 不同路径 II
第三组(状态定义和状态转移):LeetCode198. 打家劫舍、LeetCode213. 打家劫舍 II、LeetCode337. 打家劫舍 III、LeetCode309. 最佳买卖股票时机含冷冻期
第四组(0-1背包问题):LeetCode416. 分割等和子集、LeetCode322. 零钱兑换、LeetCode377. 组合总和 Ⅳ、LeetCode474. 一和零、LeetCode139. 单词拆分、LeetCode494. 目标和
第五组(LIS问题):LeetCode300. 最长递增子序列、LeetCode376. 摆动序列
第六组(各种子序列问题):LeetCode674. 最长连续递增序列、LeetCode1143. 最长公共子序列、LeetCode128. 最长连续序列、LeetCode392. 判断子序列