高等数学学习笔记

高等数学学习笔记

Part 1: 极限

  • 设函数f(x)在点(x_0)的某一去心邻域内有定义，如果存在常数A，对于任意给定的正数ε（无论它多么小），总存在正数(δ)，使得对于$$0<|x-x_0|<δ$$ 均有$$f(x)-A<ε$$

  • 那么常数A就叫做函数f(x)当时(x→x_0)的极限，记作

[lim_{x o x_0}f(x) = A ]

夹逼定理

在求函数(f(x))的极限时，可以通过两个函数夹它

举例：(lim_{x o 0}frac{sum(x)}x = 1)

易知(sin(x) < x < tan(x)), 得(cos(x) < frac{sin(x)}x < 1)

因为(displaystylelim_{x o 0} cos(x) = 1,1=1), 所以原式得证

Part 2: 导数

  • 斜率：对于一次函数(y=kx+b)斜率即为k。

  • 导数：通俗的说函数在一点的导数为在该处做切线，所得直线的斜率

[large{f'(x_0)=lim_{delta x o 0}}frac{f(x_0+delta x) - f(x_0)}{delta x} ]

  • 也可记做(frac{dy}{dx})

  • 将原函数y(x)每个点的导数全部算出后形成一个新的函数叫做原函数的导函数(y'(x))

  • 高阶导记作 (f^{(n)})

可导: 　从左侧与右侧趋近极限相同时才可定义导数

导数表：

导数

导数与函数单调性

众所周知, 导数和函数单调性有着不可分割的关系

  • 一阶导数描述增减, 一阶导等于零时, 原函数处于区间最值
  • 二阶导数描述一阶导数增减, 描述原函数的凹凸性

导数公式

四则运算:

[(u pm v)' = u' pm v'\(uv)'= u'v + v'u\(frac uv)'=frac{(u'v-v'u)}{v^2}\(C cdot f(x))'=C cdot f'(x) \(f(g(x)))'=f'(g(x)) cdot g'(x) ]

求导练习题

  • ((2x^2-3ln(x))' = 4x-frac 3x)
  • (((x^2+1)(x +2))' = (x^2+1)(1)+(2x)(x+2)=3x^2+4x+1)
  • ((sin(3x+2))'=sin'(3x+2)(3x)=3xcdot cos(3x+2))

Part 3: 洛必达法则：

若(f(x))和(g(x))在a点处为零

[large{lim_{x o a}frac{f(x)}{g(x)} = lim_{x o a}frac{frac{f(x)-f(a)}{x-a}}{frac{g(x)-g(a)}{x-a}}=lim_{x o a}frac{f'(x)}{g'(x)}} ]

洛必达法则可以多次使用, 即多次求导

Part4: 自然对数e:

[large{e=lim_{n o infty}(1+frac1n)^n=2.718281828459cdots} ]

奇妙的性质:

[f(x) = e^x~~~f'(x) = e^x\f(x) =ln~x ~~~f'(x)=frac 1x ]

Part5: 寻找方程的根: 牛顿迭代法

找方程的根首先我们可以随机两个点, 使用勘根定理, 如果(f(a)cdot f(b) leq 0)则在区间([a, b])内二分.

但是我们可能并不能很好的找到根所在的区间, 于是牛顿迭代法应运而生

牛顿迭代

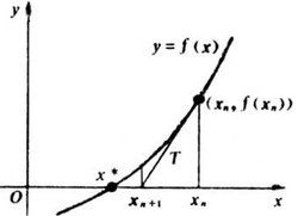
求解方程(f(x)=0), 随机一个初始点

  • 对于当前点x，做切线(求导)，计算与x轴交点作为下一轮迭代的x

  • 可得(x_{next}=x-frac{f(x)}{f’(x)})

  • (f(x)<eps)时终止，对于大部分函数有效(反例(y=frac1x 或~y=sqrt {|x|}))

Part6: 定积分

定积分

  • 求函数([a,b])区间里的有向面积，在x轴上方为正，x轴下方为负。

  • 极限法：将区域切成无数细长条，每一长条用矩形面积(f(x)*dx)近似

[S = int_a^bf(x)dx \=lim_{n o infty}sum_{0<kleq n}f(x_{k-1})*(x_k-x_{k-1})\=lim_{n o infty}sum_{0<kleq n}f(x_{k})*(x_k-x_{k-1}) ]

例: 求定积分

[int_0^cx^2dx= displaystyle lim_{n o infty}x_k^2dx ]

[原式=lim_{n o infty}(frac{ck}n)^2(frac cn)\=lim_{n o infty}(frac{c^3}{n^3})sum_{0 leq k<n}k^2\=lim_{n o infty}large{(frac{c^3(2n^3-3n^2+n)}{6n^3})}\=frac {c^3}3 ]

一般形式:

[displaystyle int_0^cx^ndx=frac{c^{n+1}}{n+1} ]

积分与微分

积分与微分可以感性的理解为升维与降维, 所以它们天生有着妙不可言的关系:

[f'(x)dx=lim_{n o infty}sum_{0 leq k < n}f(x_k)'dx\=lim_{n o infty}sum_{0 leq k < n}large{frac{f(x_{k+1})-f(x_k)}{(x_{k+1}-x_k)}(x_{k+1}-x_k)}\=lim_{n o infty}sum_{0 leq k < n}f(x_{k+1})-f(x_k)\=lim_{n o infty}f(x_{n-1})-f(x_0)=f(b)-f(a) ]

积分与无穷向量

对于一个函数(f(x))可以理解为一个无穷维的向量，每个点的函数值是一个维度，那么两个函数(f(x))和(g(x))的内积就可以理解为(int f(x)g(x)dx)

Part 7: 自适应Simpson积分法

前置:求二次函数区间内的有向面积;

  • 见定积分基本内容

二次函数拟合积分法:

[int^b_af(x)dx approx frac{b-a}6(f(a)+4f(frac{a+b}2)+f(b) ]

可以使用自适应法控制精度问题

inline double simpson(double a, double b) {
    return (b - a) * (f(a) + f(b) + 4 * (f(((a+b)/2)))) / 6;
}

double eps = 1e-6;
double solve(double l, double r, double A, double eps) {
    double mid = (l + r) / 2;
    double L = simpson(l, mid), R = simpson(mid, r);
    if (fabs(L+R-A) <= 15 * eps) return L + R + (L+R-A) / 15.0;
    return solve(l, mid, L, eps / 2) + solve(mid, r, R, eps / 2);
}

应用: 在求解计算几何中的面积问题时

可以建立坐标系, 将面积化为一个函数, 求圆等圆滑的图形, 函数是平滑的, 但积分法无法解决一段函数全为零的情况, 所以提前判断有值的两端端点进行积分

Part8:函数最优化

二元函数

给定多元函数(f(x) o R), 求f(x)最小值

爬山法, 随机方向, 随机步长, 只向更优解走

如果函数存在导数, 有更好的方法, 如(f(x)=sin(x_1)cos(x_2))

求偏导 :相当于定住其他变量, 求单一变量的导数

  • 对于二元函数(f(x,y))，在((x_0,y_0))处固定y不变切片移动x，可以得到一个单变量函数(g(x))，同理固定x不变可以得到(h(y))，可以定义某一个方向的导数

  • 求导时只需将另一个变量当做常数即可。

偏导练习

  • ((x^2+1)(y+2))
  • (large{frac{sin^2(frac3y)+ln(cos ~xy)}{x^5e^y}})

偏导数与梯度

  • 梯度：(delta f(x,y)= (frac{delta f}{delta x}, frac{delta f}{delta y}))

  • 函数值上升最快的方向？

    (f(x + dx, y + dy) approx f(x, y) + frac{delta f}{delta x}dx+frac{delta f}{delta y}dy)

  • 单位圆上寻找((dx,dy))使得其与梯度的内积最大

  • 显然((dx,dy))与梯度共线时增长最快

无约束函数极值

给定多元函数(f(x)→R)，其中x是n维向量，寻找使得函数值最小的向量x*。

代入偏导数为0的极值条件解方程：(delta f(x)=0)

如: 求(min f(x) = (x_1-x_2-2)^2+(x_2-1)^2)

[delta f(x) = largeleft(^{frac{delta f}{delta x_1}}_{frac{delta f}{delta x_2}} ight)= left( ^{~~~~~~~~2(x_1-x_2-2)}_{-2(x_1-x_2-2)+2(x_2-1)} ight) = left(^0_0 ight) ]

Part 9: 拉格朗日乘数法

设给定多元函数(ƒ(x))和附加条件(phi(x)=0)，x为向量，为寻找z=ƒ(x)在附加条件下的极值点，构造拉格朗日函数(L(x, lambda)=f(x)+lambdaphi(x))

此时有：

[min_x=min_x{max_{lambda}L(x, lambda)}=min_x{max_{lambda}f(x)+lambdaphi(x)} ]

f(x)为最优的必要条件是拉格朗日函数L梯度为0：

由上述方程组解出x，就是函数z=ƒ(x)在附加条件φ(x)=0下可能的极值点。

例：

求(x,y,z)使得((x-4)^2+y^2+z^2)最小，并且(x+y+z=3, 2x+y+z=4)

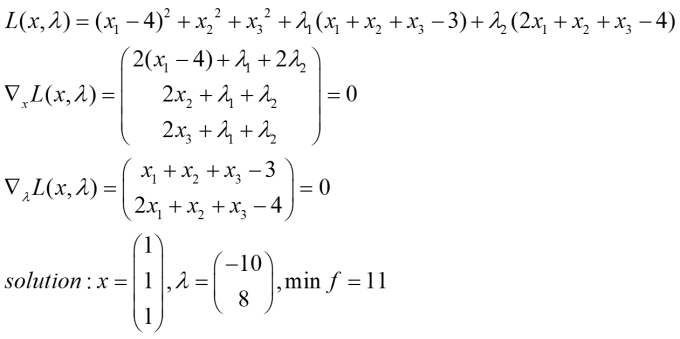
1AJmh6.md.png

Part10: 泰勒展开

[f(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + a_3(x - x_0)^3 + ...\f(x) approx f(0) + frac{f'(0)}{1!}x+frac{f''(0)}{2!}x^2+cdots+frac{f^{(n)}}{n!}x^n ]

n趋于正无穷时, 将几乎完全拟合

证明:

[f(x) - f(0) = int_0^{x}f'(x)dx\f'(x) - f'(0)=int_0^xf''(x)dx\f(x) = f(0) + int_0^{x}f'(x)dx\= f(0) + int_0^{x}left(int_0^xf''(x)dx + f'(0) ight)dx\= f(0) + int_0^{x}int_0^xf''(x)dx^2 + int_0^xf'(0)dx\= f(0) + int_0^{x}int_0^xf''(x)dx^2 + frac{f'(0)}{1!}x ]

将二次导, 三次导等带入即可用数学归纳法证明

常见泰勒展开

1ANrHH.png

欧拉公式: (e^{i heta}=cos( heta)+isin( heta))

可用泰勒展开证明

【推广】 免费学中医，健康全家人
原文地址：https://www.cnblogs.com/Hs-black/p/12228919.html