该系列为DR_CAN自动控制原理视频笔记，详见https://space.bilibili.com/230105574
由于笔者水平有限，文中难免存在一些不足和错误之处，诚请各位批评指正。
1 理解分离/汇合点
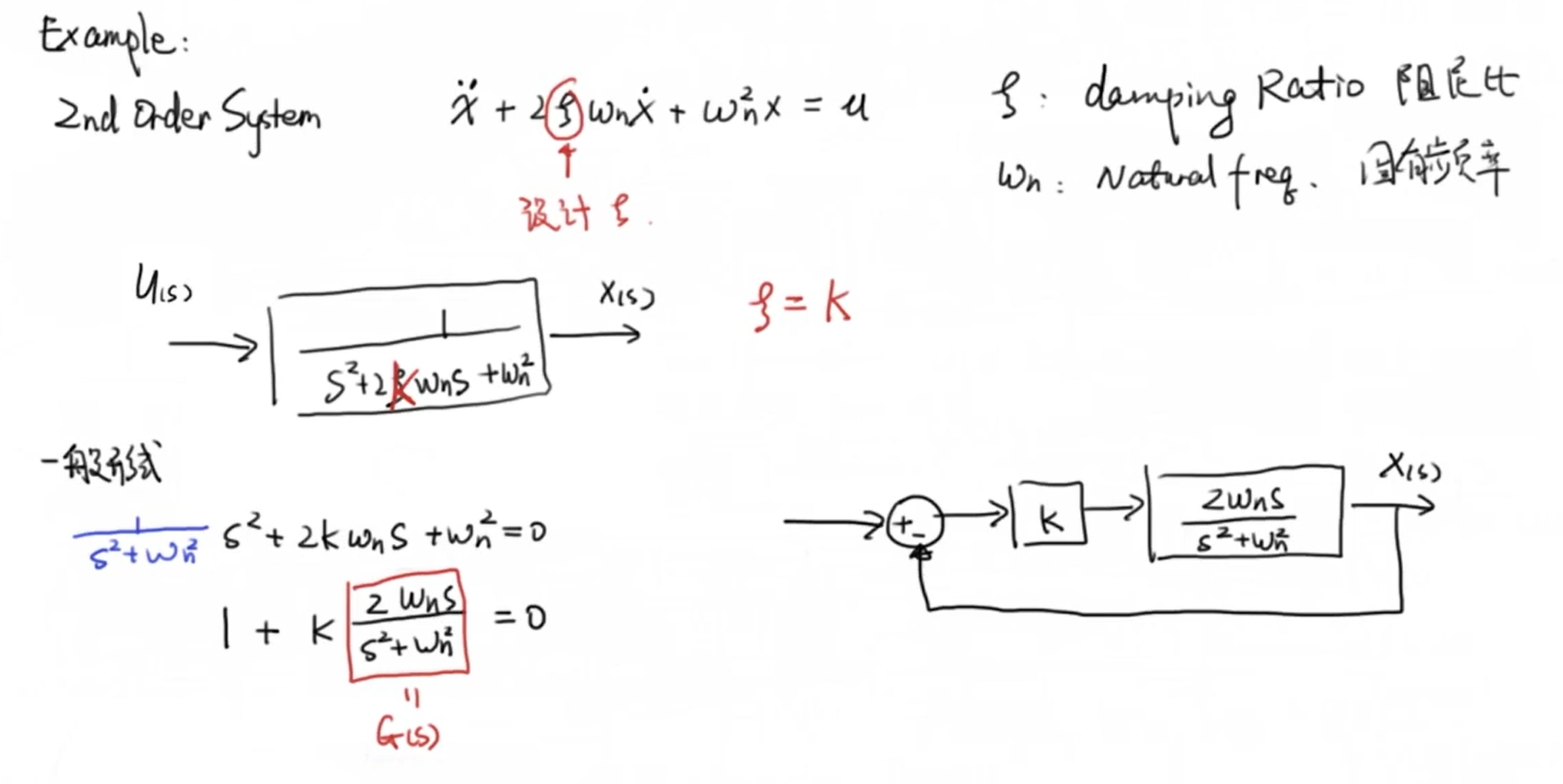
这里以二阶系统为例，我们希望通过根轨迹法设计系统的阻尼比 (zeta) ，即可令 (zeta=k) 。绘制根轨迹前我们需要先将传递函数的分母部分化位一般形式，并绘制出等效的系统框图：
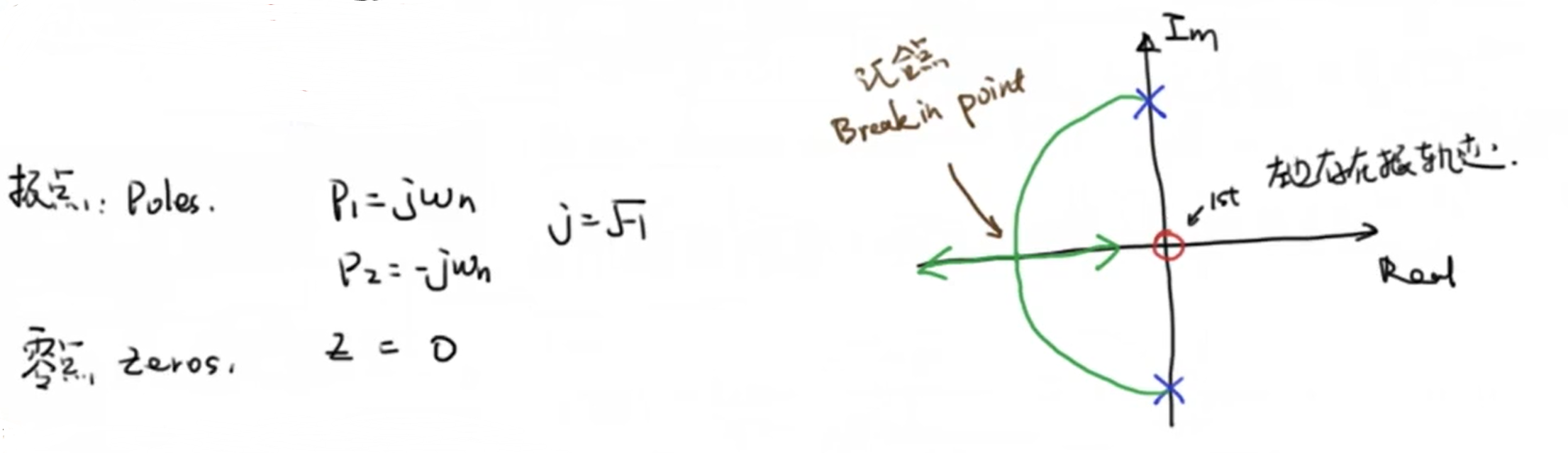
我们可以计算出系统的两个极点和一个零点，他们均在虚轴上。极点比零点多一个，因此会有一个极点指向零点一个极点指向负无穷，另外的，根轨迹关于实轴对称，因此我们可以得到下面的结果：
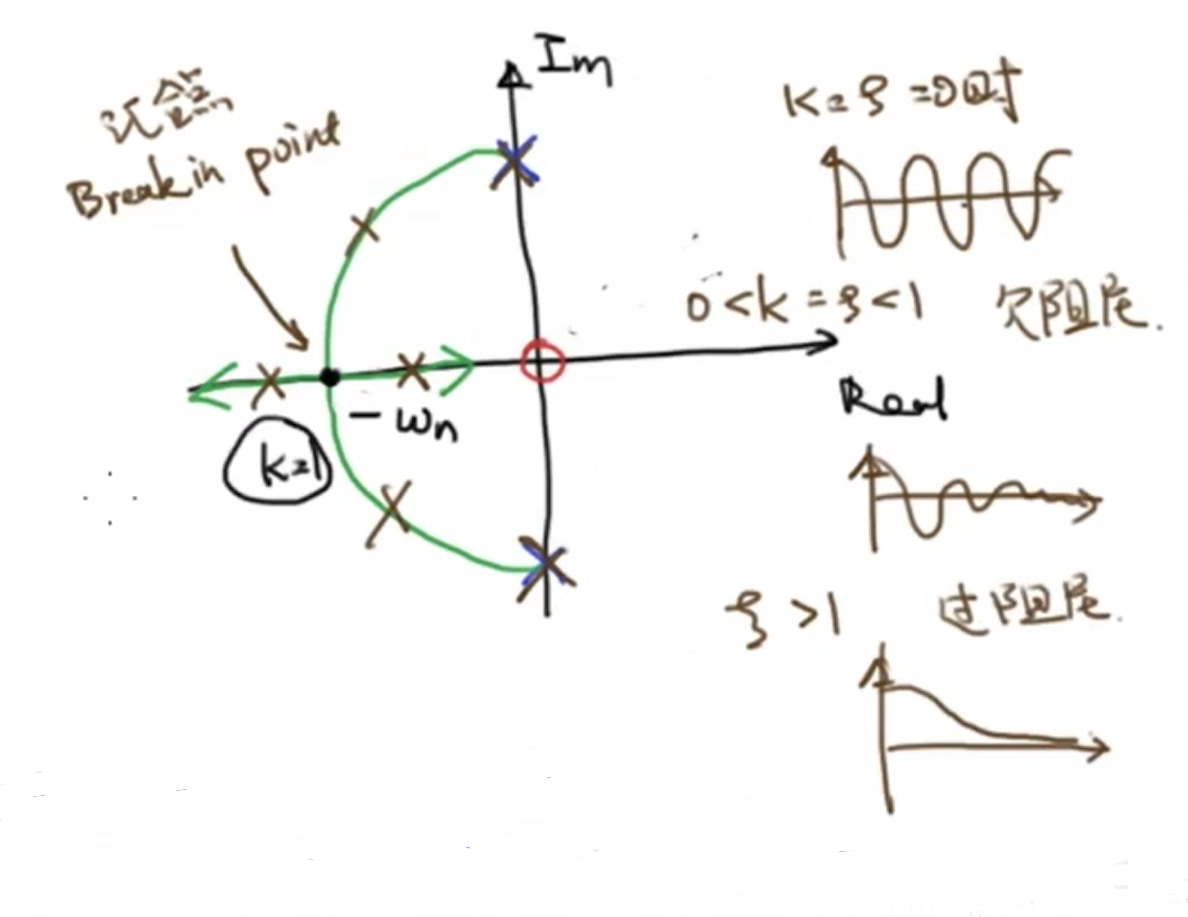
接下来我们来计算这个汇合点的位置，通过对刚才的等式进行变形可以把 (k) 写成 (s) 的函数的形式。我们优质的这个汇合点在实轴上，因此 (s) 的虚部为0，即 (s = sigma) ，这样一来了 (k) 就变成了 (sigma) 的函数。接下来我们对 (sigma) 求一阶导，可以分析 (k) 的极值，而 (k) 的极值一定是 (s) 离开实轴的点。经过计算我们可以算出(sigma = pm omega_n) 是 (k) 的极值，将 (sigma = -omega_n) 带回表达式可以求出 (k=1) ：
这时我们带着这个结论，和 (k) 从0增大到正无穷的过程中根会有极点运动的零点的性质，来结合二阶系统的冲激响应进一步分析这个二阶系统的根轨迹，考虑到二阶系统冲激响应我们已经很熟悉了这里不再赘述：
2 根轨迹的性质
先回顾一下复数的一点性质：
观察下面这个例子，我们发现：将一个 (s) 代入分子或分母得到的结果，他的模长和幅角与零点或极点到这个 (s) 的向量是完全相同的：
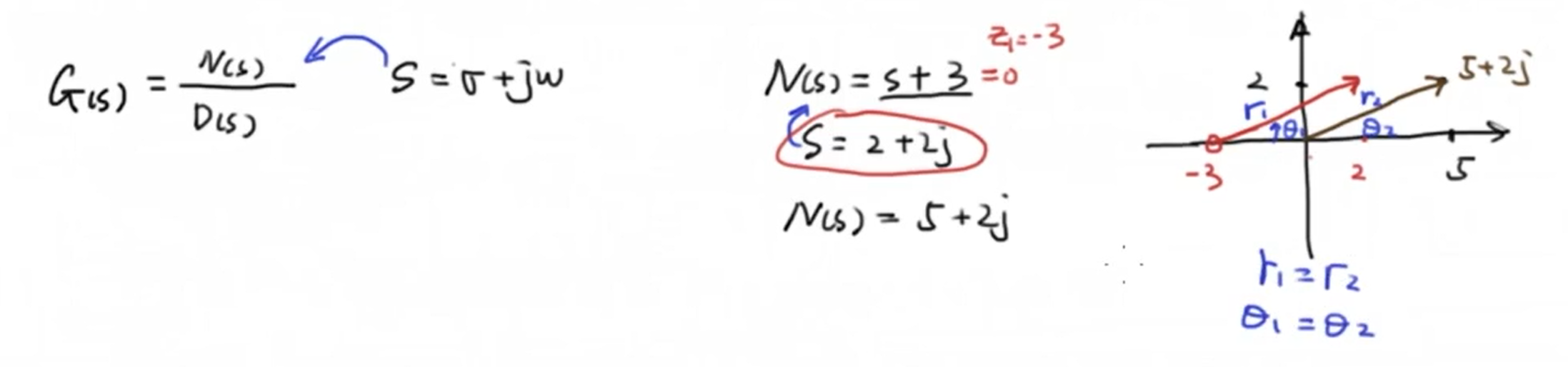
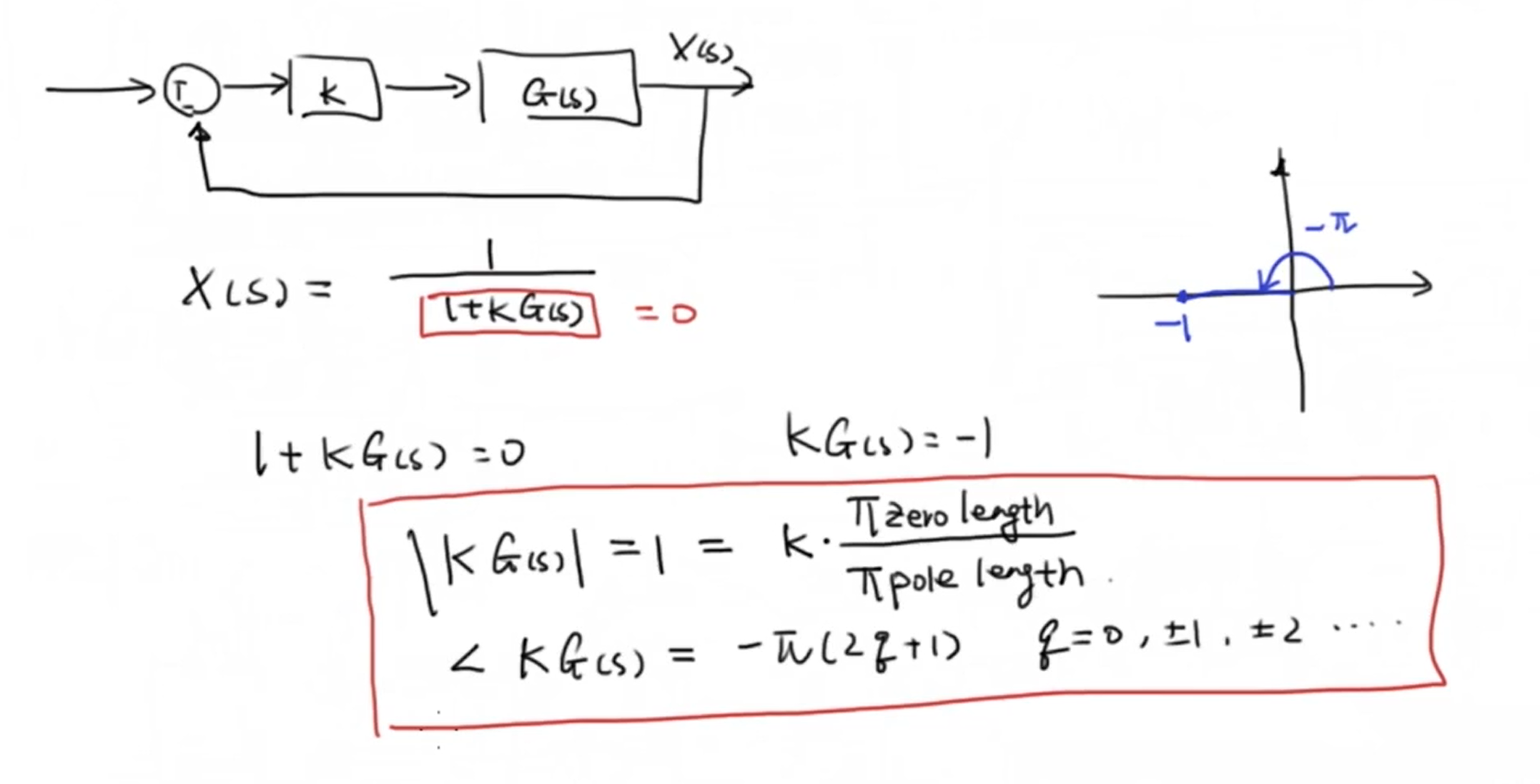
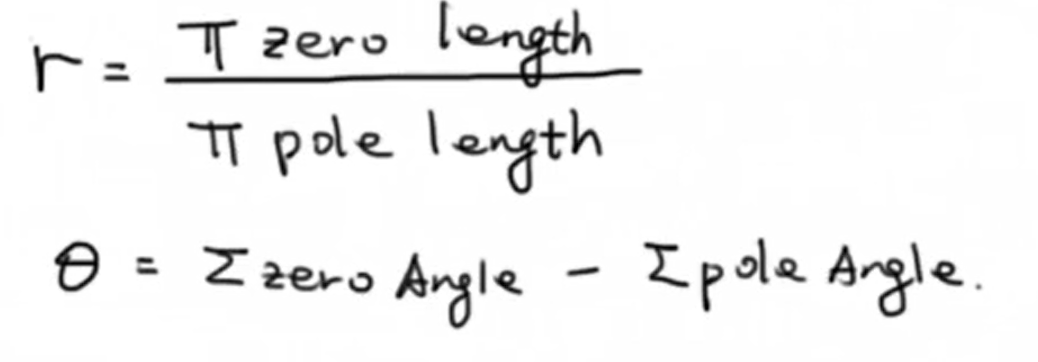
因此将复数代入传递函数我们有这样的结论， 我们把 (s) 代入传递函数后的结果的幅值等于所有零点到这个复数 (s) 距离的积，比上所有极点到这个复数的距离的积，而结果的幅角则等于所有零点与这个复数的夹角和，减去所有极点与这个复数的夹角和。即：
这么说有些晦涩难懂我们来看一个例子：
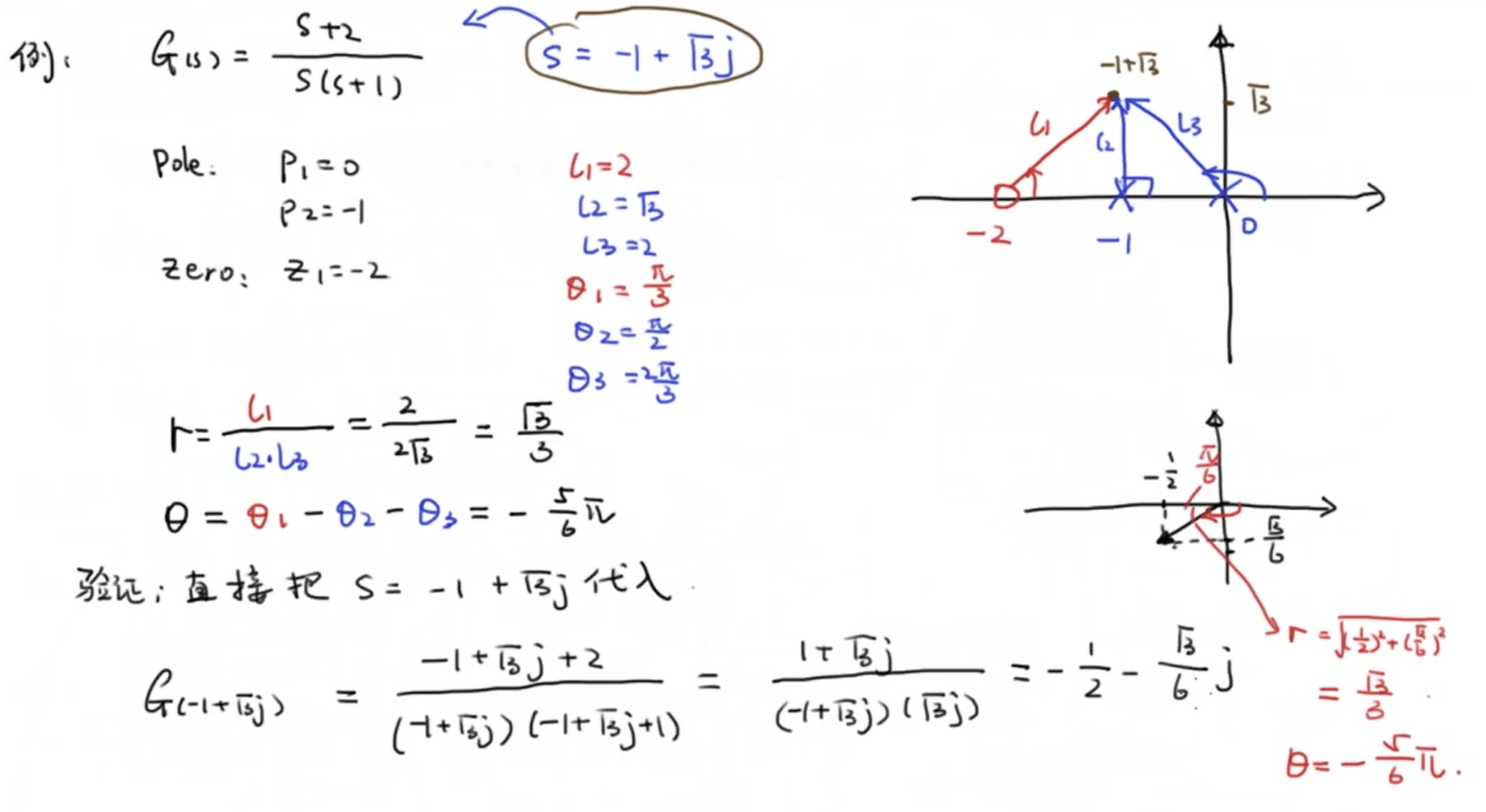
这样一来，我们就可以通过这种几何的方法很轻松的进行计算了。另外的，这种几何的方法也给后面设计控制器打下了基础。
通过这种方法我们再来回到根轨迹。从根轨迹的标准形式中我们可以看到这个轨迹是 (kG(s)=-1) ，这是一个模长为1幅角为 (pi) 的复数，通过上面的几何方法，我们可以判断一个复数是否在根轨迹当中，也可以用来进一步设计控制器，具体使用再之后会讲到。
