该系列为DR_CAN动态系统的建模与分析系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 定义
拉普拉斯变换(英语:Laplace transform)是应用数学中常用的一种积分变换,又名拉氏转换,其符号为 (mathcal{L}{f(t)}) 。拉氏变换是一个线性变换,可将一个有实数变量 (t (t>0)) 的函数转换为一个变量为复数的 (s) 函数:
2 电路的例子
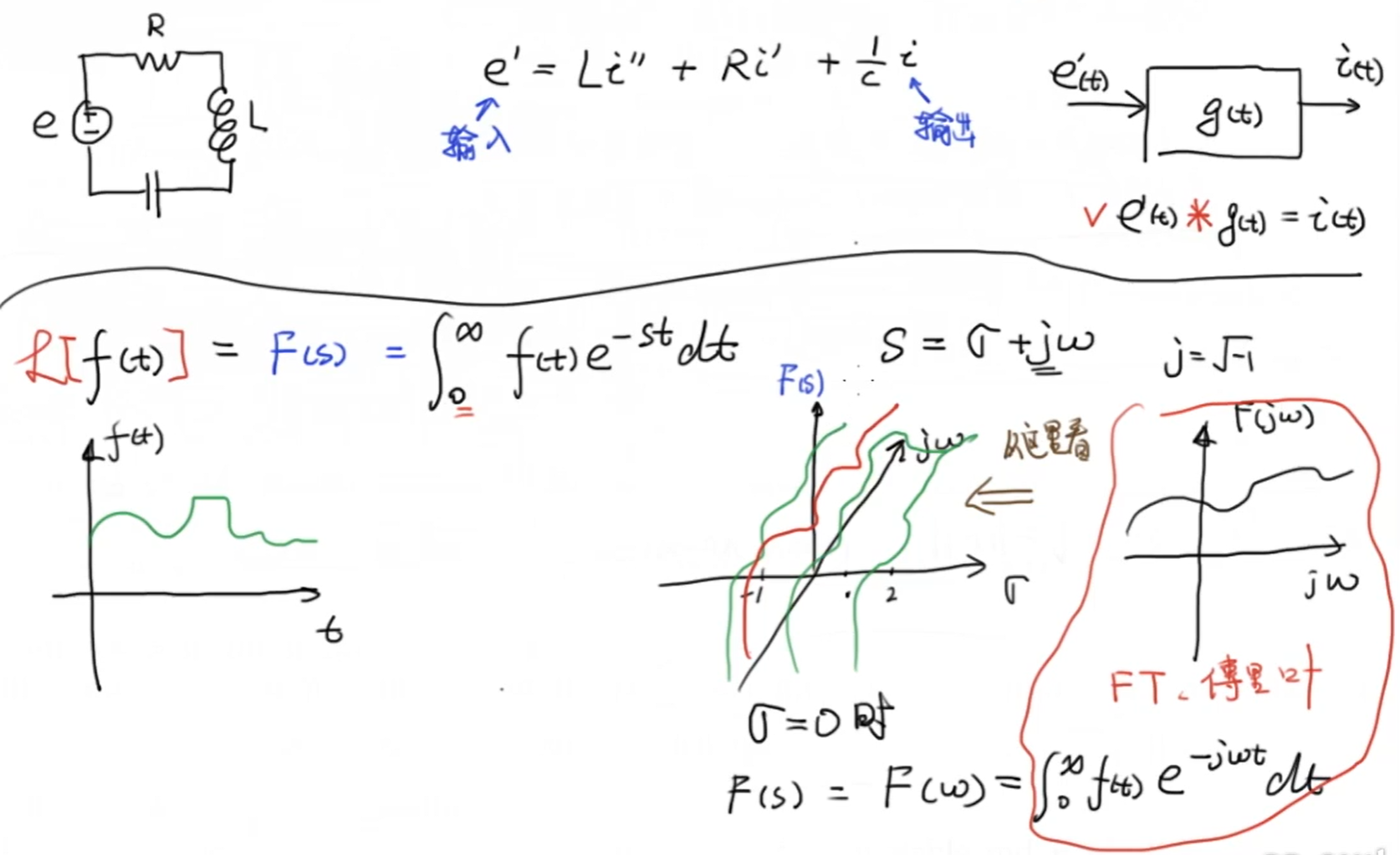
分析这个电路系统的输入(电压)与输出(电流)的关系,实际上就需要我们对这个微分方程进行求解。如果我们用一个系统框图来表示,这个变化过程 (g(t)) 就包含着这个系统的特征,也就是微分方程所包含的内容。通过对 (e'(t)) 与 (g( t )) 进行卷积运算可以得到 (i(t)) 。但这样分析和计算都相对复杂,这时我们就需要借助拉普拉斯变换,将微分方程转换成代数方程、卷积运算转换为乘法运算。
对时域函数 (f(t)) 做拉普拉斯变换的公式如下图中表示,这将二维平面上的曲线变换为了三维复空间中的曲面。当我们沿观察 (sigma) 轴观察 (F(s)Ojomega) 平面,即 (sigma = 0) 时,图像就变成了在虚轴上的一条曲线,而拉普拉斯变换就变成了另一个我们熟悉形式,也就是傅里叶变换。
而当我们沿着 (F(s)) 轴观察 (sigma O jomega) 平面时,我们往往会关注图像也就是这个系统的极点与零点,进而对系统进行分析。
3 指数函数的例子
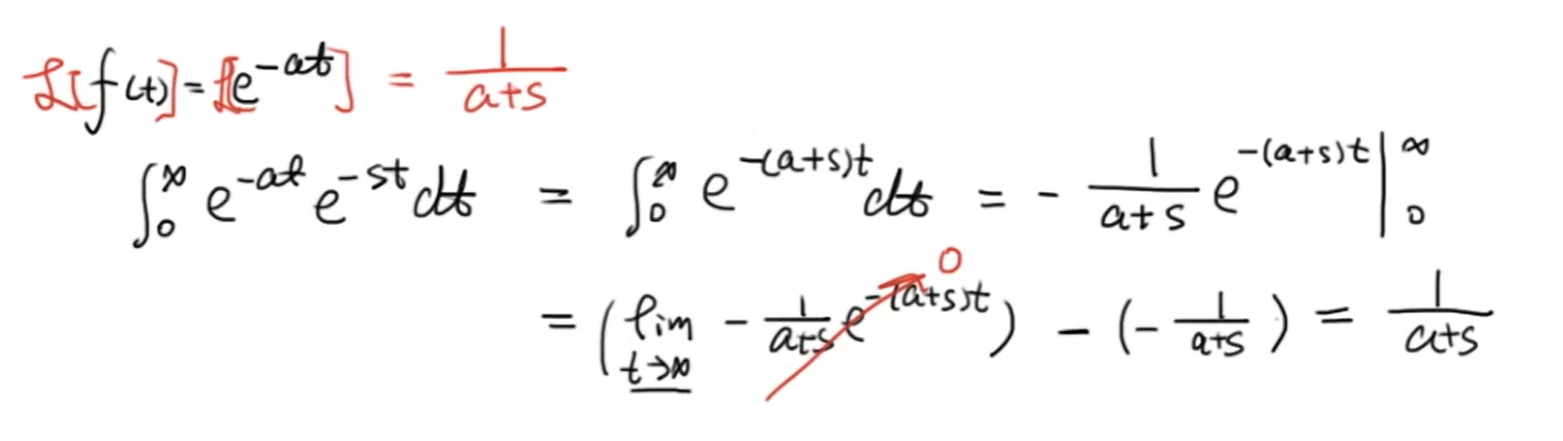
4 性质
- 线性:

- 积分与导数的拉普拉斯变换:
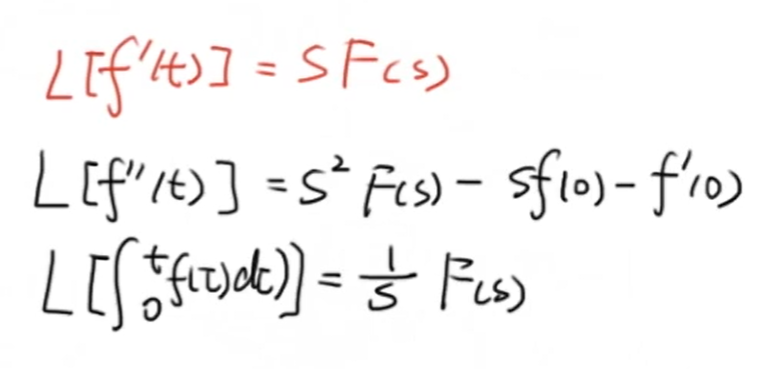
其中,导数的拉普拉斯变换推导如下:
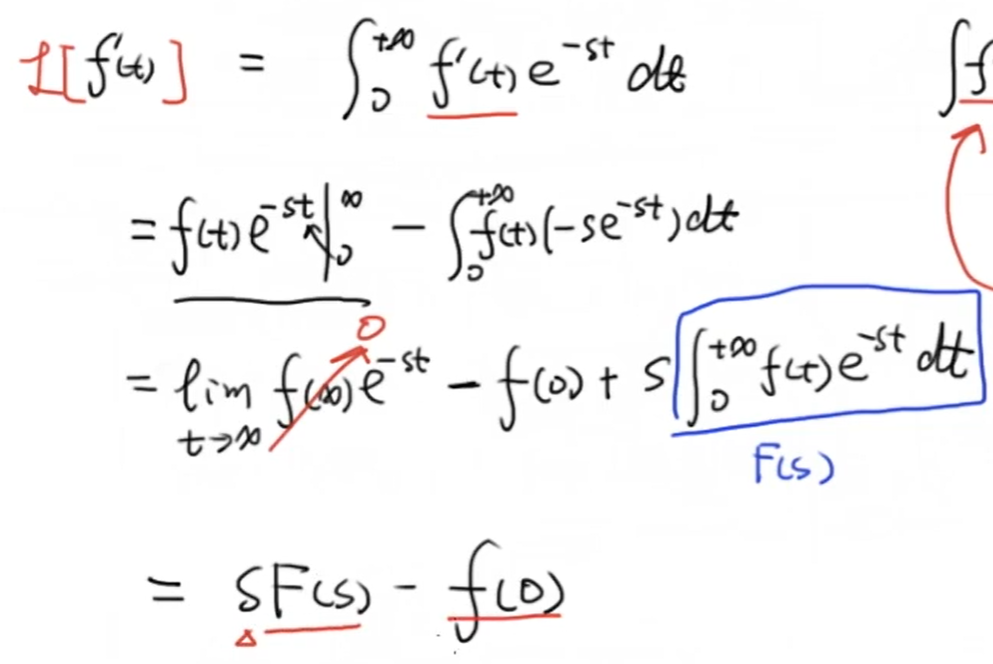
一般情况下我们将系统的初始条件设置为0,因此 (f(0) = 0) 即可忽略。
5 回到电路的例子
通过拉普拉斯变换,我们可以对刚刚电路系统的微分方程进行变换:
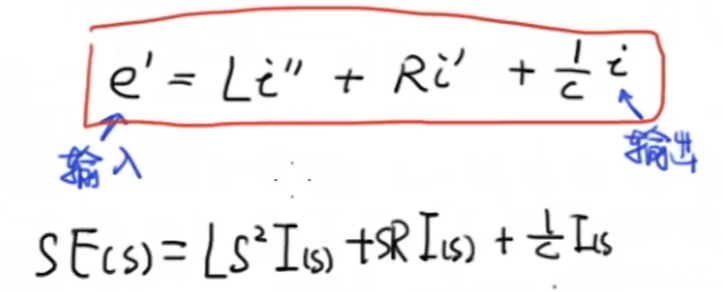
经过整理可得:
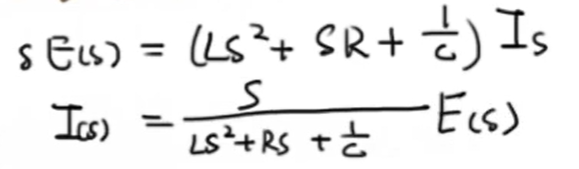
这样一来,我们就把一个微分方程转换成了一个仅含有加减乘除的代数方程。
其中:
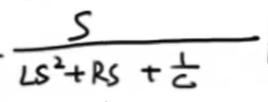
就是所谓的系统传递函数。