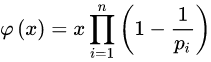什么是欧拉函数?
引用百科上的原话,在数论中,对任意正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目(一般认为 φ(1) = 1)。此函数以其首名研究者欧拉命名(Euler's totient function),它又称为Euler's totient function、φ函数、欧拉商数等。 例如φ(8)=4,因为1,3,5,7均和8互质。 从欧拉函数引伸出来在环论方面的事实和拉格朗日定理构成了欧拉定理的证明。
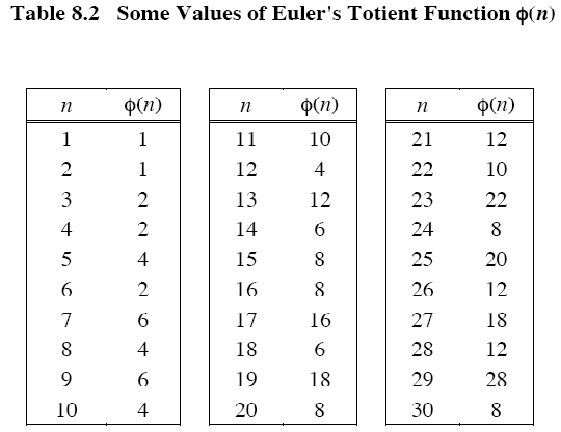
下面是30以内数字的欧拉函数的值:
重要定理
p和q是互素的数字, n=p*q, φ(n)= φ(p)φ(q)。 特别地,若p和q都是素数,则有 φ(n) = (p-1)(q-1)。
证明:
考虑余数集合{0, 1, …, (pq-1)}中不与n互素的余数集合是{p, 2p, …, (q-1)p}, {q, 2q, …, (p-1)q}和0, 所以 φ(n)= pq-[(q-1)+(p-1)+1]=pq-(p+q)+1= (p-1)(q-1)=φ(p)φ(q)
函数通式
其中p1, p2,…,pn为x的所有质因数,x是正整数。
证明:

定理
n>2时候,φ(n)一定为偶数。
证明:
从函数通式可以看出,满足p > 2的时候,每一个子式中的 p - 1 一定是偶数(p是素数啊),而假设存在p1 = 2,(p_1^{e_i-1}(p_1-1))也一定是偶数(最小是0)。故欧拉函数φ(n)可以视为t项偶数的和,φ(n)一定也是偶数。