INTRODUCTION:
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,
实际应用时一般还要开4N的数组以免越界,因此有时需要离散化让空间压缩。--百度百科
给定一个有100000个元素的数组,并给出10000个操作,操作分为两种:
1.将数组中的第l个到第r个元素全部加上k
2.输出第l元素到第r个元素的总和
对于这类对区间进行修改与查询的题,数据范围往往极大,所以暴力往往是不可行的,因此就要用到线段树这种高效的区间修改与查询数据结构了
那么线段树有什么优势呢?
1.动态:相对其他只支持查询的数据结构,线段树不但支持查询,还支持修改(单点修改与区间修改),并且这两种操作的时间复杂度都相当低
2.全能:线段树同时支持区间查询与区间修改,单点查询与单点修改,不但可以维护区间内所有元素的和,还可以维护区间最大值等等可以代替
多种其他数据结构,当然时间复杂度可能会稍大一些
3.快速:线段树继承了树形数据结构的优势,无论是查询还是修改,时间复杂度都是O(logn)
那么接下来以支持区间查询与区间修改(给一个一个区间内的所有元素都增加或减少k)的线段树为例:
首先:给定一个原数组a[4]={1,2,3,4};
那么,他对应的一颗线段树是这样的:
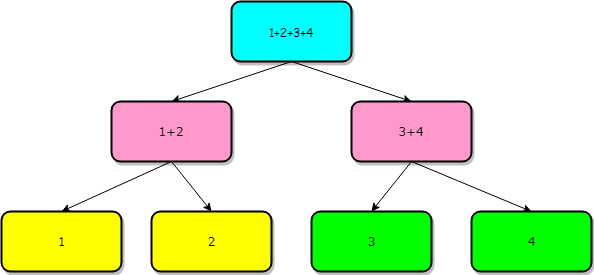
如图所示,根节点表示区间【1,4】的值之和,而他的两个儿子节点则分别表示区间【1,2】以及区间【3,4】的值之和
叶子节点则分别表示区间【1,1】,【2,2】,【3,3】,【4,4】的值
如果把根节点想象成一条长为4cm的线段,那么他的两个儿子节点就像是两条长为2cm的线段,四个叶子节点就像是四根长为1cm的线段
由此一来,我们就将一根长为4cm(【1,4】)的线段,先劈成了两根长为2cm的线段(【1,2】,【3,4】) ,又将他们劈成了四根长为1cm的线段(【1,1】,【1,2】,【1,3】【1,4】),借助这些线段,我们就可以快速的查询每一个区间的和(比如区间【1,4】直接对应根节点【1,4】,区间【1,3】对应【1,2】+【3,3】
每一个要查询的区间都可以对应线段树中的一个节点,或多个节点之和),线段树也因此得名。
那么,我们该如何将一个数组转化为一棵线段树呢?那么我们首先需要一个表示线段树节点的结构体并经行一段建树函数:
线段树结构体:
1 struct tree
2 {
3 int left;//区间的左端点
4 int right;//区间的右端点
5 int sum;//区间【left,right】的和
6 int add;//懒标记。之后用到
7 }t[400004];//注意大小要开到原数组的4倍以上
建树函数:
1 void build(int rt, int l, int r)
2 {
3 t[rt].left = l;//记录左端点
4 t[rt].right = r;//记录右端点
5 if (l == r)//如果左端点等于右端点
6 {
7 t[rt].sum = a[l];//则代表区间【l,l】也就等价于a【l】,直接记录这段区间的值即可
8 return;//之后return,作为递归出口
9 }
10 int mid = (l + r) / 2;//二分
11 build(rt * 2, l, mid);//构建他的左儿子
12 build(rt * 2 + 1, mid + 1, r);//构建他的右儿子
13 t[rt].sum = t[rt * 2].sum + t[rt * 2 + 1].sum;//根节点的值等于左右儿子节点的值之和
14 }
那么如何进行区间查询呢?
对于要查询的区间【l,r】,我们从树根向下进行查找,如果找到一个节点,使他所代表的区间包含于【l,r】,那么自然要将这个节点的值,不过由于不能保证要查询的区间一定精准对应树上的某个节点,所以在查询到每一个节点时,一旦他不完全属于待查询区间,就要通过递归来查询他的左右子树,直到递归得到的区间完全包含于待查询区间,这些区间的值之和就是待查询区间的值,代码实现很简单:
区间查询:
1 int search_sum(int rt, int l, int r)//区间查询
2 {
3 if (l <= t[rt].left && t[rt].right <= r)//如果该区间完全包含于待查询区间
4 return t[rt].sum;//那么直接返回他的值,作为递归出口
5 down(rt);//下传懒标记,之后用到
6 int mid = (t[rt].left + t[rt].right) / 2;//二分
7 int ans = 0;
8 if (l <= mid)
9 ans += search_sum(rt * 2, l, r);//查找左子树
10 if (r > mid)
11 ans += search_sum(rt * 2 + 1, l, r);//查找右子树
12 return ans;//最终返回这些区间的和
13 }
之后是区间修改:
其实区间修改与区间查询很像,只需要根据区间查询的思想递归修改被修改区间的值就行了、
不过这样显然是不行的,因为这样修改的时间复杂度为O(n),比暴力做法都要慢一些,所以显然不可行的
因此就要引入懒标记了:
当我想要修改区间【l,r】,使他增加k时,我们只需要找到【l,r】对应的区间,然后打上一个标记表示该区间的每一个元素都增大了k,着时候如果想要查询【l,r】自然很容易
但是如果我要查询【l,r】的子区间,由于懒标记只标记了【l,r】并没有标记他的子区间,所以这个子区间的值并没有被修改,这时候查询他显然会出错。
所以必须存在一种操作,就是下传懒标记,从而修改他的子区间的值,这样就可以保证不会出错了
下传懒标记:
1 void down(int rt)//下传懒标记
2 {
3 if (t[rt].add)//只有在存在懒标记时才下传
4 {
5 t[rt * 2].sum += t[rt].add * (t[rt * 2].right - t[rt * 2].left + 1);//每一个元素都增大k,所以整体增大了k*元素个数
6 t[rt * 2 + 1].sum += t[rt].add * (t[rt * 2 + 1].right - t[rt * 2 + 1].left + 1);//分别处理左右子树
7 t[rt * 2].add += t[rt].add;//这是懒标记已经传递到了两颗子树上
8 t[rt * 2 + 1].add += t[rt].add;//修改子树的懒标记的值
9 t[rt].add = 0;//该节点的懒标记的值改为0
10 }
11 }
引入懒标记后,区间修改的时间复杂度就降低到了O(logn)
区间修改:
1 void change(int rt, int l, int r, int k)//区间修改
2 {
3 if (l <= t[rt].left && t[rt].right <= r)
4 {
5 t[rt].sum += k * (t[rt].right - t[rt].left + 1);//修该区间的值
6 t[rt].add += k;//修改懒标记
7 return;
8 }
9 down(rt);//下传懒标记
10 int mid = (t[rt].left + t[rt].right) / 2;//分别处理左右子树
11 if (l <= mid)
12 change(rt * 2, l, r, k);
13 if (r > mid)
14 change(rt * 2 + 1, l, r, k);
15 t[rt].sum = t[rt * 2].sum + t[rt * 2 + 1].sum;//回溯时修改祖先节点的值
16 }
下面是完整代码:
1 #include<iostream>
2 #include<algorithm>
3 #include<string.h>
4 #if !defined(_WIN32)
5 #include<bits/stdc++.h>
6 #endif // !defined(_WIN32)
7 #define ll long long
8 using namespace std;
9 ll n, m;
10 struct tree
11 {
12 ll sum;//区间和
13 ll add;//加号懒标记
14 ll left;//左儿子
15 ll right;//右儿子
16 }t[500005];//线段树的结点
17 ll a[100086];
18 void build(ll root, ll l, ll r)//递归建树
19 {
20 t[root].left = l;
21 t[root].right = r;
22 if (l == r)
23 {
24 t[root].sum = a[l];//如果我细化到一个点
25 return;//那我就已经建好了,return就好
26 }
27 ll mid = (l + r) / 2;
28 build(root * 2, l, mid);//递归左半部分
29 build(root * 2 + 1, mid + 1, r);//递归右半部分
30 t[root].sum = t[root * 2].sum + t[root * 2 + 1].sum;
31 }
32 void down(ll rt)
33 {
34 if (t[rt].add)
35 {
36 t[rt * 2].sum += t[rt].add * (t[rt * 2].right - t[rt * 2].left + 1);
37 t[rt * 2 + 1].sum += t[rt].add * (t[rt * 2 + 1].right - t[rt * 2 + 1].left + 1);
38 t[rt * 2].add += t[rt].add;
39 t[rt * 2 + 1].add += t[rt].add;
40 t[rt].add = 0;
41 }
42 }
43 void change(ll rt, ll l, ll r, ll k)
44 {
45 if (l <= t[rt].left && t[rt].right <= r)
46 {
47 t[rt].sum += k * (t[rt].right - t[rt].left + 1);
48 t[rt].add += k;
49 return;
50 }
51 down(rt);
52 ll mid = (t[rt].left + t[rt].right) / 2;
53 if (l <= mid)
54 change(rt * 2, l, r, k);
55 if (r > mid)
56 change(rt * 2 + 1, l, r, k);
57 t[rt].sum = t[rt * 2].sum + t[rt * 2 + 1].sum;
58 }
59 ll search(ll rt, ll l, ll r)
60 {
61 if (l <= t[rt].left && t[rt].right <= r)
62 return t[rt].sum;
63 down(rt);
64 ll ans = 0;
65 ll mid = (t[rt].left + t[rt].right) / 2;
66 if (l <= mid)
67 ans += search(rt * 2, l, r);
68 if (r > mid)
69 ans += search(rt * 2 + 1, l, r);
70 return ans;
71 }
72 int main()
73 {
74 cin >> n >> m;
75 for (int i = 1; i <= n; i++)
76 cin >> a[i];
77 build(1, 1, n);
78 for (int i = 1; i <= m; i++)
79 {
80 int t;
81 cin >> t;
82 if (t == 1)
83 {
84 ll x, y, k;
85 cin >> x >> y >> k;
86 change(1, x, y, k);
87 }
88 else
89 {
90 ll x, y;
91 cin >> x >> y;
92 cout << search(1, x, y) << endl;
93 }
94 }
95 return 0;
96 }
当然线段树还有很多其他的妙用,比如说查询区间最大值(RMQ问题)等等
RMQ
1 #include<iostream>
2 #include<algorithm>
3 #include<cstdio>
4 using namespace std;
5 int n, m;
6 struct tree
7 {
8 int left;
9 int right;
10 int Max;
11 }t[400004];
12 int a[100086];
13 void build(int rt, int l, int r)//建树
14 {
15 t[rt].left = l;
16 t[rt].right = r;
17 t[rt].Max = -20041001;
18 if(l==r)
19 return ;
20 int mid = (l + r) / 2;
21 build(rt * 2, l, mid);
22 build(rt * 2 + 1, mid + 1, r);
23 }
24 int search_max(int rt, int l, int r)
25 {
26 if (l <= t[rt].left && t[rt].right <= r)
27 return t[rt].Max;
28 int mid = (t[rt].left + t[rt].right) / 2;
29 int ans = -20041001;
30 if (l <= mid)
31 ans = max(ans, search_max(rt * 2, l, r));
32 if (r > mid)
33 ans = max(ans, search_max(rt * 2 + 1, l, r));
34 return ans;
35 }
36 void insert(int rt, int i, int x)
37 {
38 t[rt].Max = max(t[rt].Max, x);
39 if (t[rt].left != t[rt].right)
40 {
41 int mid = (t[rt].right + t[rt].left) / 2;
42 if (i <= mid)
43 insert(rt * 2, i, x);
44 else
45 insert(rt * 2 + 1, i, x);
46 }
47 }
48 int main()
49 {
50 cin >> n >> m;
51 build(1, 1, n);
52 for (int i = 1; i <= n; i++)
53 {
54 int x;
55 cin >> x;
56 insert(1, i, x);
57 }
58 for (int i = 1; i <= m; i++)
59 {
60 int x, y;
61 cin >> x >> y;
62 cout << search_max(1, x, y) << endl;
63 }
64 return 0;
65 }
