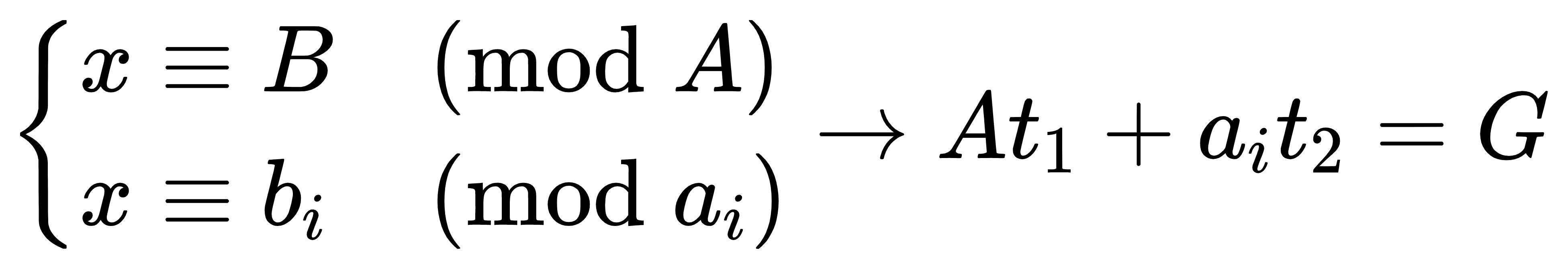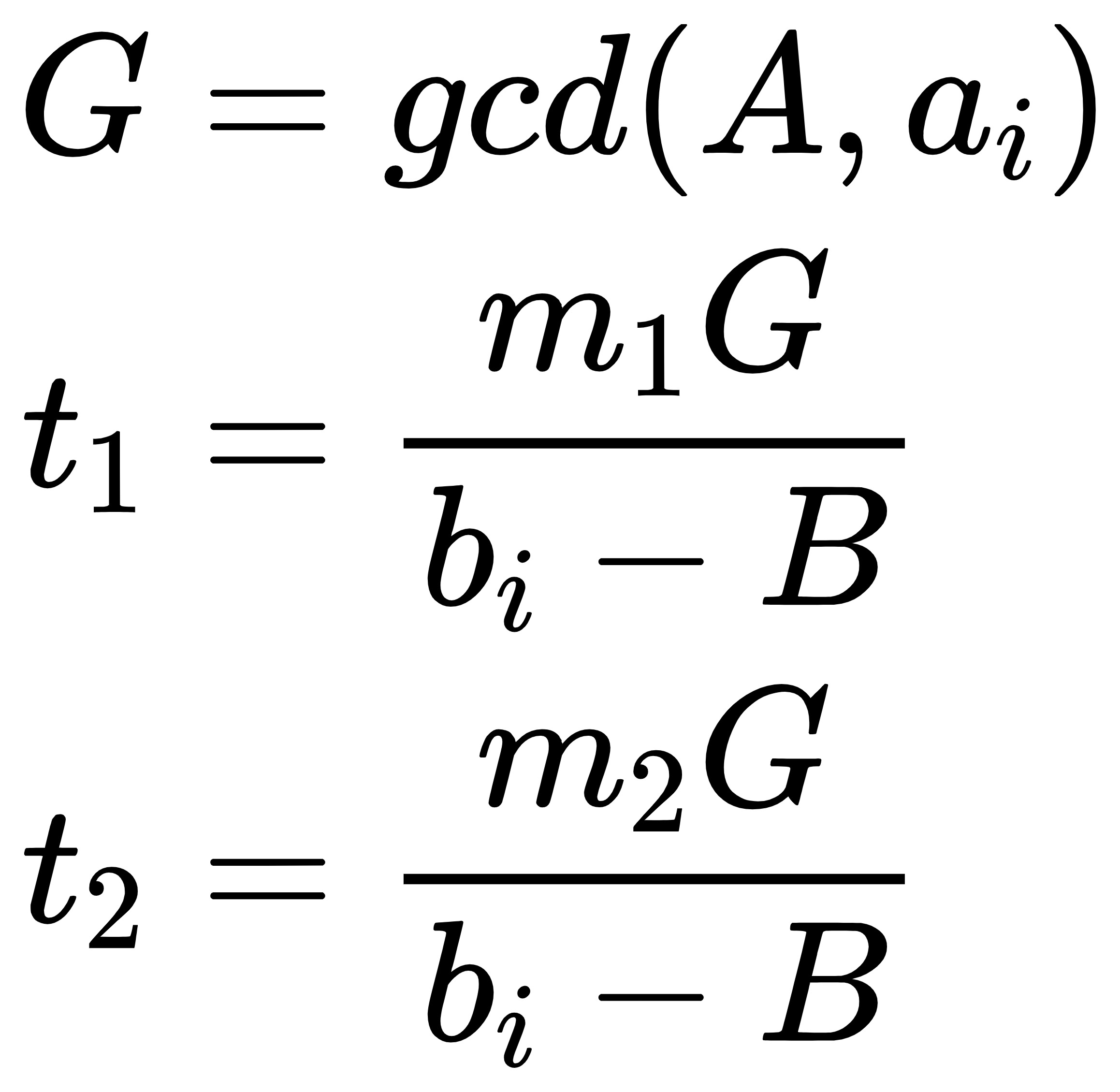这里是一些常用的板子合集
快读:
int read() { int s=0,f=1;char a=getchar(); while(a<'0' || a>'9') { if(a=='-') f=-1; a=getchar(); } while(a>='0' && a<='9') { s=s*10+a-'0'; a=getchar() ; } return f*s; }
拓欧:
int exgcd (int a,int b ,int& x,int& y) {//函数将返回(gcd(a,b)) if(b==0) { x=1,y=0; return a; } int sum=exgcd(b,a%b,y,x) y-=(a/b)*x; return sum; }
拓欧扩欧傻傻分不清楚
前置:拓欧
扩欧求逆元:
int inv(int sum,int mod) {//注意:sum与mod必须互质 exgcd(sum,mod,x,y); return (x%mod+mod)%mod; }
快速幂:
long long qkpow(LL base,LL indexx)//MOD为模数,题目不要去去掉即可 qkpow=quickpow { long long sum=1; while(indexx>0) { if((indexx&1)!=0) sum=sum*base%MOD; base=base*base%MOD; indexx>>=1; } return sum%MOD; }
前置:快速幂
费马小定理求逆元(模数为质数):
long long inv(long long sum) { return qkpow(sum,mod-2) }
线性筛:
void shai() {
//zhi是存质数的数组,he是判断当前数是否为合数的bool数组 scanf("%d%d",&n,&k); he[1]=true; for(int i=2;i<=n;i++) { if(he[i]!=true) { zhi[++cnt]=i; } for(int j=1;j<=cnt&&i*zhi[j]<=100000001;j++) { he[i*zhi[j]] = true ; if(i%zhi[j]==0) break; } } }
前置:线性筛
线性递推乘法逆元:
inv[1]=1; //m为模数
for(int i=2;i<=n;i++) { inv[i]=((-m/i)*inv[m%i]%m+m)%m; }
待增加:
拓展欧拉定理:
![]()
中国剩余定理
阶乘法求乘法逆元
快写
待删改高斯消元:
#include<bits/stdc++.h> using namespace std; int n; const double x=0.000001; bool vis[200]; double a[200][20000]; double d[200]; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { scanf("%lf",&a[i][j]); } scanf("%lf",&d[i]); } for(int k=1;k<=n;k++) { int to; for(int i=1,maxn=-0x7fffffff;i<=n;i++)//找最大 { if(a[i][k]>maxn&&vis[i]==false) { maxn=a[i][k]; to=i; } } if(0-x<=a[to][k]&&a[to][k]<=0+x) { printf("No Solution"); return 0; } double chu=a[to][k]; swap(d[1],d[to]); swap(vis[1],vis[to]); vis[1]=true; d[1]/=chu; for(int i=1;i<=n;i++) { swap(a[1][i],a[to][i]); a[1][i]/=chu; } for(int i=2;i<=n;i++) { chu=a[i][k]/a[1][k]; double t; for(int j=k;j<=n;j++) { t=a[1][j]*chu; a[i][j]=a[i][j]-t; } double dt=d[1]*chu; d[i]=d[i]-dt; } } for(int k=1;k<=n;k++) { for(int i=1;i<=n;i++) { if(1-x<=a[i][k]&&a[i][k]<=1+x) { printf("%.2lf\n",d[i]); break; } } } return 0; }
龟速乘:
long long slow_mul(long long a,long long b,long long mod) { long long ans=0; while(b!=0) { if((b&1)>0) { ans+=a; ans%=mod; } a=a+a; a%=mod; b=b>>1; } return ans; }
拓展中国剩余定理: