1.树
需要注意的两点:n(n>=0)表示结点的个数,m表示子树的个数
(1)n>0时,树的根节点是唯一的。
(2)m>0时,子树的个数没有限制。
结点的度和树的度
(1)结点的度是指结点拥有的子树数
(2)树的度是指树的各结点的度的最大值
树的深度(Depth)
树中结点的最大层次
1
/
2 3
/
4 5 6
此树的深度是3

树和图有什么区别?
树其实就是不包含回路的连通无向图。
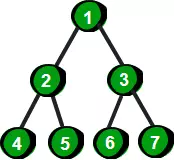

上面这个例子中左边的是一棵树,而右边的是一个图。因为左边的没有回路,而右边的存在1->2->5->3->1这样的回路。
(1)正是因为树有着“不包含回路”这个特点,所以树就被赋予了很多特性。
(2)一棵树中的任意两个结点有且仅有唯一的一条路径连通。
(3)一棵树如果有n个结点,那么它一定恰好有n-1条边。
2.二叉树
特点:
(1)每个结点最多有两棵子树
(2)左子树和右子树都是有顺序的,次序不能任意颠倒
(3)即使树中某结点只有一颗子树,也要区分是左子树还是右子树
1
3
3就是1的右子树
二叉树的常见性质:
性质1 在二叉树的第i层上至多有2i-1个结点(i>=1)
性质2 深度为k的二叉树至多有2k-1个结点(k>=1)
性质3 满二叉树,在一棵深度为k且有2k-1个结点。完全二叉树,若一棵深度为k的二叉树,其前k-1层是一个棵满二叉树,而最下面一层(即第k层)上的结点都集中在该层最左边的若干位置上。
性质4 对于任何一棵二叉树T,如果其终端结点数(叶子结点数)为n0,度为2的结点数为n2,则n0=n2+1
性质5 具有n个结点的完全二叉树的深度为[log2n]+1
栗子1:
具有300个结点的二叉树,其高度(深度)至少为9
9层:至多:29-1=512-1=511
8层:至多:28-1=256-1=255
栗子2:
已知一颗7层完全二叉树的第6层(设根是第1层)有8个叶结点,则该完全二叉树的结点个数最多是多少?
第6层至多有26-1=32个,因为有8个叶结点,所以有24个子结点。又因为是完全二叉树,则第7层最多有24*2=48个叶结点。
前6层至多26-1=63个,所以该完全二叉树的结点数最多是48+63=111

解释:
完全二叉树里叶子节点只能出现在层次最大的两层上出现。
所以假设有两种情况。
1.这棵树最大层次是8.前七层为满二叉树,第八层剩余10个叶子节点。sum=27-1+10=137
2.这棵树最大层次为9,前八层为满二叉树,第八层里有10个节点没有子树,sum=28-1+(28-1-10)*2=491
栗子3:
一个具有20个叶子节点的二叉树、它有()个度为2的节点
可知n0=20,由n0=n2+1,可以得到n2=19
栗子4:
设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1,则T中的叶子数为()
又由于 n = n0 + n1 + n2 + n3 + n4 = n0 + 8;
n0 + 8 = 16,所有叶子结点个数为8
栗子5:
对于有n个结点的二叉树,其高度为()
正确答案: D
A.nlog2n
B.log2n
C.[log2n]+1
D.不确定
解释:如果是完全二叉树则是[log 2 n]+1,有计算公式。其他的二叉树没有规律,是没有计算公式的,也是不确定的,只能知道其高度的范围是:[log2n ]+1 到 n
栗子6:
完全二叉树共有700结点,该二叉树有多少个叶子结点?
对于二叉树总的结点数是:n=n0+n1+n2
由性质4知,n0=n2+1
所以,n0+n1+n0-1=700,又n1只能去0或1,故此处选1
2n0=700,n0=350
完全二叉树和满二叉树
二叉树的两种存储结构
(1)顺序存储(一般只用于完全二叉树)适用性不强
对于完全二叉树而言,可以使用顺序存储结构。但是对于一般的二叉树来说,使用存储结构会有两个缺点:
一、如果不是完全二叉树,则必须将其转化为完全二叉树,
二、是增加了很多虚节点,浪费资源空间。

(2) 链式存储
这是最常用的一种二叉树存储结构。
每个结点设置三个域,即值域,左指针域和右指针域,用data表示值域,lchild和rchild分别表示指向左右子树的指针域。如图所示。

遍历二叉树
前,中,后序遍历,这个前、中、后都是相对于根节点而言的,都是从根节点出发,按照某种次序一次访问二叉树中的所有结点,使得每个结点被访问的次数有且只有一次
前序遍历(先根遍历):根-->左-->右
中序遍历(中根遍历):左-->根-->右(左,是从最下层结点的左子树开始遍历)
后序遍历(后根遍历):叶子-->结点-->根节点(按照先左子树,后右子树,最后访问根节点)
层序遍历:从树的第一层,也就是根节点开始访问,从上到下一层一层遍历,其中在同一层,就按照从左到右的顺序访问

前序遍历:
12-9-76-35-22-16-48-46-40-90-
中根遍历:
9--12--16--22--35--40--46--48--76--90--
后根遍历:
9---16---22---40---46---48---35---90---76---12---
实现代码:二叉树的创建和遍历都是利用了递归的思想
package package2;
public class BinaryTree {
int data; //根节点数据
BinaryTree left; //左子树
BinaryTree right; //右子树
public BinaryTree(int data) //实例化二叉树类
{
this.data = data;
left = null;
right = null;
}
public void insert(BinaryTree root,int data){ //向二叉树中插入子节点
if(data>root.data) //二叉树的左节点都比根节点小
{
if(root.right==null){
root.right = new BinaryTree(data);
}else{
this.insert(root.right, data);//利用了递归
}
}else{ //二叉树的右节点都比根节点大
if(root.left==null){
root.left = new BinaryTree(data);
}else{
this.insert(root.left, data);//利用了递归
}
}
}
}
/*当建立好二叉树类后可以创建二叉树实例,并实现二叉树的先根遍历,中根遍历,后根遍历,代码如下:*/
package package2;
public class BinaryTreeTraverse {
public static void preOrder(BinaryTree root){ //先根遍历
if(root!=null){
System.out.print(root.data+"-");
preOrder(root.left);
preOrder(root.right);
}
}
public static void inOrder(BinaryTree root){ //中根遍历
if(root!=null){
inOrder(root.left);
System.out.print(root.data+"--");
inOrder(root.right);
}
}
public static void postOrder(BinaryTree root){ //后根遍历
if(root!=null){
postOrder(root.left);
postOrder(root.right);
System.out.print(root.data+"---");
}
}
public static void main(String[] str){
int[] array = {12,76,35,22,16,48,90,46,9,40};
BinaryTree root = new BinaryTree(array[0]); //创建二叉树
for(int i=1;i<array.length;i++){
root.insert(root, array[i]); //向二叉树中插入数据
}
System.out.println("先根遍历:");
preOrder(root);
System.out.println();
System.out.println("中根遍历:");
inOrder(root);
System.out.println();
System.out.println("后根遍历:");
postOrder(root);
}
}
3.推导遍历结果
三种情况:
(1)已知前序遍历和中序遍历,可以唯一确定一棵二叉树
(2)已知后序遍历和中序遍历,可以唯一确定一棵二叉树
(3)已知前序遍历和后序遍历,是不能确定一棵二叉树的
推导方法:
(1)先确定根节点。可以根据前序的第一个元素或后序的最后一个元素来确定
(2)确定第一个根节点的左子树和右子树。可以根据中序来确定
栗子1:
已知前序ABCDEF,中序CBAEDF,还原此二叉树,并推出中序遍历的结果
(1)首先确定根节点是A,根据前序的第一个元素。
(2)由中序可知,A的左边是CB,右边是EDF
A
/
B D
/ /
C E F
可推出后序:CBEFDA
栗子2:
已知中序ABCDEFG,后序BDCAFGE,还原此二叉树,并推出中序遍历的结果
(1)首先确定根节点是E,根据后序的最后一个元素。
(2)由中序可知,E的左边是ABCD,右边是FG
初步判断:
E
/
ABCD FG
再次判断:
E
/
A G
/
C F
/
B D
可推出前序:EACBDGF
栗子3:某二叉树的先根遍历序列和后根遍历序列正好相反,则该二叉树具有的特征是(A)
A.高度等于其结点数
B.任一结点无左孩子
C.任一结点无右孩子
D.空或只有一个结点
解释:
可以是全部都是左孩子,也可以是全部都是右孩子,所以在一起就合称高度等于其结点数
A A
/
B B
/
C C
/
D D
先根遍历是:A-B-C-D 先根遍历是:A-B-C-D
后根遍历是:D-C-B-A 后根遍历是:D-C-B-A
4.哈夫曼树
哈夫曼树是一种带权路径长度最短的二叉树,也称为最优二叉树。
(1)什么叫带权路径长度?
从该结点到树根之间路径长度与结点上的权的乘积
下面用一幅图来说明。
它们的带权路径长度分别为:
图a: WPL=5*2+7*2+2*2+13*2=54
图b: WPL=5*3+2*3+7*2+13*1=48
可见,图b的带权路径长度较小,我们可以证明图b就是哈夫曼树(也称为最优二叉树)
(2)如何构建哈夫曼树?
一般可以按下面步骤构建:
(1)将所有左,右子树都为空的作为根节点。
(2)在森林中选出两棵根节点的权值最小的树作为一棵新树的左,右子树,且置新树的附加根节点的权值为其左,右子树上根节点的权值之和。注意,左子树的权值应小于右子树的权值。
(3)从森林中删除这两棵树,同时把新树加入到森林中。
(4)重复2,3步骤,直到森林中只有一棵树为止,此树便是哈夫曼树。
下面是构建哈夫曼树的图解过程:

(3)哈夫曼编码
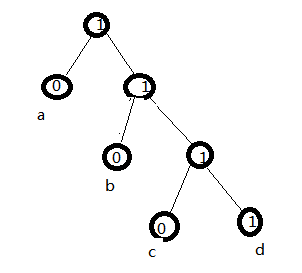
利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。
树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
就拿上图例子来说:
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
用图说明如下:
注意:若有编码00,则至少必须有编码01,否则只一个结点构成不了双亲,也就是说,不是二叉树了。
如:00,100,101,110,111不可能是哈夫曼编码
记住,设计电文总长最短的二进制前缀编码,就是以n个字符出现的频率作为权构造一棵哈夫曼树,由哈夫曼树求得的编码就是哈夫曼编码。
栗子1:
用二进制来编码字符串"abcdabaa",需要能够根据编码,解码回原来的字符串,最少需要多长的二进制字符串?
解析:哈夫曼编码问题。求二进制字符串长度其实就是求带权最短路径长度。
可以先构造哈夫曼树,字符串中,a有4个,b有2个,c有1个,d有1个,这些个数就是权值,先选最小的两个权值,c和d,
如图:
所以字符串总长度:4*1+2*2+1*3+1*3=14
栗子2:
已知一段文本有1382个字符,使用了1382个字节进行存储,这段文本全部是由a、b、c、d、e这5个字符组成,a出现了354次,b出现了483次,c出现了227次,d出现了96次,e出现了232次,对这5个字符使用哈夫曼(Huffman)算法进行编码,则以下哪些说法正确()ACD
A.使用哈夫曼算法编码后,用编码值来存储这段文本将花费最少的存储空间
B.使用哈夫曼算法进行编码,a、b、c、d、e这5个字符对应的编码值是唯一确定的
C.使用哈夫曼算法进行编码,a、b、c、d、e这5个字符对应的编码值可以有多套,但每个字符编码的位(bit)数是确定的
D.b这个字符的哈夫曼编码值位数应该最短,d这个字符的哈夫曼编码值位数应该最长
解释:
栗子3:
一棵哈夫曼树共有215个结点,对其进行哈夫曼编码,共能得到(108)个不同的码字
解释:
这个题目其实就是求有多少个叶子结点,就是度数为0的结点,因为哈夫曼树是二叉树,而且哈夫曼树中一定没有度数为1的结点。
由n=n0+n2,和n0=n2+1,可以得到n2=107,所以n0=108
栗子4:给字母重新进行二进制编码,以使得"MT-TECH-TEAM"(包含连字符,不包含引号)的长度最小.并能够根据编码,解码回原来的字符串.请问最优编码情况下该字串的长度是多少bit?
解释:哈夫曼编码,统计每个单词出现的次数,进行排序,每次合并最小的两个,把合并的值带入,删除原来的两个值后,继续排序,直到最后只剩下一棵树
M:2 H:1
T:3 A:1
E:2 -:2
C:1

参考文档:
http://blog.sina.com.cn/s/blog_70600f720100ujnp.html
http://www.cnblogs.com/mcgrady/p/3329825.html