题意
对于一个(n imes m)的矩形,每个方格都有一个颜色。
令其价值为:相邻同色两点连边后,其连通块个数。
例如
AAB
BBA
BBB
其价值为(4),四个连通块分别为
..B AA. ... ...
... ... BB. ..A
... ... BBB ..
给定一个(n imes m)的矩形,每个方格都有一个颜色,用大写字母表示,(q)次询问,每次给定(x_1,y_1,x_2,y_2(1le x_1le x_2le n,1le y_1le y_2le m)),输出这个矩形的价值。
(n,m,qle 1000)
做法
相邻同色点连边后,这是一个平面图,而我们求的是连通块个数
在题目中,矩形中的一个块是描述的一个颜色,为以下我们称为的点
在题目中,矩形中两个相邻块有公共边,但以下我们是点与点间的边,要分清楚
比如,样例
ABBAAAAA
ABAAAABA
CAADABBA
AAAAAAAA
形成的平面图是这样样子的:
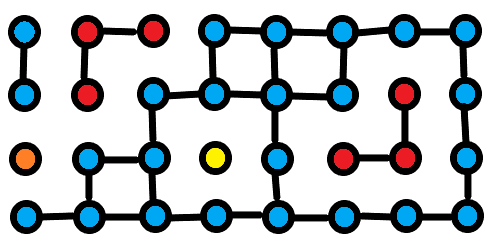
欧拉公式:在平面图内,令(V)为点个数,(F)为面个数,(E)为边个数,(C)为连通块个数,有(F+V-E=C+1)
证明:
考虑特殊情况,连通块个数为(1)的情况,若我们能证明(F+V-E=2),那么多个连通块也同理。
选出该连通块任意生成树,考虑该平面图的对偶图,对偶图两个点存在连边,当且仅当该连边不穿过生成树。
考虑我们得到的对偶图,一定是无环的,若有环,则必定将某两点分割开了,显然与之前得到的生成树矛盾,那么也容易得到这个对偶图是连通的。
生成树的点数为(V),对偶图的点数为(F),容易知道其边数和为(E),有树的定义我们得到(V+F=E+2)。
得证。
有欧拉公式得到(V=V+F-E-1),那么转化为求(V,F,E)
(V)即为((x_2-x_1+1)(y_2-y_1+1)),边可以通过(O(nm))预处理,通过前缀和(O(1))计算。
现在难点在于求面数(F)。
考虑一个完整的矩形,如何求面数?
令([i,j])为以点((i,j))为左上角的方格,以([i,j])为位置,然后进行遍历,找到围住这个方格可能的四条边,判断哪条边不存在,若不存在则可前往那个点。注意若([i,j])可以走出这个矩形,说明是外面的那个无界面。
我们对于这个完整的矩形,每个面(除无界面),任选一个方格记为关键点,对于查询,查询内部的关键点个数(也可以通过前缀和优化)。
此时遇到一个问题,一个面,在完整的矩形内是有界面,但在这个子矩形中是无界面,如何解决呢?
我们遍历外面这圈红色的方格,查看其关键点是否被统计过(是否关键点包含在子矩形内部),因为这圈红色的相对于这个子矩阵是无界面,然后减去

code
如果不理解可以看下代码,下面的代码未统计无界面,故在统计答案的时候,(C=V+F-E)
#include<bits/stdc++.h>
typedef int LL;
typedef double dl;
#define opt operator
#define pb push_back
#define pii std::pair<LL,LL>
const LL maxn=1e3+9,mod=998244353,inf=0x3f3f3f3f;
LL Read(){
LL x(0),f(1); char c=getchar();
while(c<'0' || c>'9'){
if(c=='-') f=-1; c=getchar();
}
while(c>='0' && c<='9'){
x=(x<<3ll)+(x<<1ll)+c-'0'; c=getchar();
}return x*f;
}
void Chkmin(LL &x,LL y){
if(y<x) x=y;
}
void Chkmax(LL &x,LL y){
if(y>x) x=y;
}
LL add(LL x,LL y){
return x+=y,x>=mod?x-mod:x;
}
LL dec(LL x,LL y){
return x-=y,x<0?x+mod:x;
}
LL mul(LL x,LL y){
return 1ll*x*y%mod;
}
LL Pow(LL base,LL b){
LL ret(1); while(b){
if(b&1) ret=mul(ret,base); base=mul(base,base); b>>=1;
}return ret;
}
const LL dx[]={0,-1,0,1,0},dy[]={0,0,1,0,-1};
LL n,m,key,q;
LL bel[maxn][maxn],fk[maxn][maxn],fe[2][maxn][maxn],mark[maxn][maxn];
LL vis[maxn*maxn<<1];
pii pos[maxn*maxn<<1];
char s[maxn][maxn];
void Bfs(LL sx,LL sy){
std::queue<pii> que;
que.push(pii(sx,sy));
fk[sx][sy]=1;
mark[sx][sy]=1;
++key; pos[++key]=pii(sx,sy);
bel[sx][sy]=key;
LL flag(0);
while(que.size()){
LL x(que.front().first),y(que.front().second);
que.pop();
for(LL i=1;i<=4;++i){
LL xx(x+dx[i]),yy(y+dy[i]);
if(x==xx){
if((s[x][std::max(y,yy)]==s[x+1][std::max(y,yy)])) continue;
}else{
assert(y==yy);
if((s[std::max(x,xx)][y]==s[std::max(x,xx)][y+1])) continue;
}
if(xx<1 || xx>n || yy<1 || yy>m){
flag=1;
continue;
}
if(!mark[xx][yy]){
bel[xx][yy]=key;
mark[xx][yy]=1;
que.push(pii(xx,yy));
}
}
}
if(flag){
fk[sx][sy]=0;
pos[key]=pii(0,0);
}
}
void Init(){
for(LL i=1;i<n;++i){
for(LL j=1;j<m;++j){
if(!mark[i][j]){
Bfs(i,j);
}
}
}
for(LL i=1;i<=n;++i){
for(LL j=2;j<=m;++j){
fe[0][i][j]=s[i][j]==s[i][j-1];
}
}
for(LL i=2;i<=n;++i){
for(LL j=1;j<=m;++j){
fe[1][i][j]=s[i][j]==s[i-1][j];
}
}
for(LL i=1;i<=n;++i){
for(LL j=1;j<=m;++j){
for(LL k=0;k<2;++k){
fe[k][i][j]+=fe[k][i-1][j]+fe[k][i][j-1]-fe[k][i-1][j-1];
}
fk[i][j]+=fk[i-1][j]+fk[i][j-1]-fk[i-1][j-1];
}
}
}
LL Getsum(LL sum[][maxn],LL lx,LL ly,LL rx,LL ry){
if(lx>rx || ly>ry) return 0;
return sum[rx][ry]-sum[lx-1][ry]-sum[rx][ly-1]+sum[lx-1][ly-1];
}
LL In(LL nw,LL lx,LL ly,LL rx,LL ry){
if(lx>rx || ly>ry) return 0;
LL x(pos[nw].first),y(pos[nw].second);
return lx<=x && x<=rx && ly<=y && y<=ry;
}
int main(){
n=Read(); m=Read(); q=Read();
for(LL i=1;i<=n;++i){
scanf(" %s",s[i]+1);
}
Init();
while(q--){
LL lx(Read()),ly(Read()),rx(Read()),ry(Read());
LL V((rx-lx+1)*(ry-ly+1));
LL E(Getsum(fe[0],lx,ly+1,rx,ry)+Getsum(fe[1],lx+1,ly,rx,ry));
LL F(Getsum(fk,lx,ly,rx-1,ry-1));
for(LL i=lx;i<=rx;++i){
if(!vis[bel[i][ly-1]] && In(bel[i][ly-1],lx,ly,rx-1,ry-1)){
--F; vis[bel[i][ly-1]]=1;
}
if(!vis[bel[i][ry]] && In(bel[i][ry],lx,ly,rx-1,ry-1)){
--F; vis[bel[i][ry]]=1;
}
}
for(LL i=ly;i<=ry;++i){
if(!vis[bel[lx-1][i]] && In(bel[lx-1][i],lx,ly,rx-1,ry-1)){
--F; vis[bel[lx-1][i]]=1;
}
if(!vis[bel[rx][i]] && In(bel[rx][i],lx,ly,rx-1,ry-1)){
--F; vis[bel[rx][i]]=1;
}
}
printf("%d
",V+F-E);
for(LL i=lx;i<=rx;++i){
vis[bel[i][ly-1]]=vis[bel[i][ry]]=0;
}
for(LL i=ly;i<=ry;++i){
vis[bel[lx-1][i]]=vis[bel[rx][i]]=0;
}
}
return 0;
}
`