根据 Polya 定理,答案为:
\[|X / G| = \frac{1}{|G|}\sum\limits_{g \in G} |B| ^ {c(g)}
\]
只需要求出置换的个数和所有置换的贡献和即可。
首先不难发现要按照点双分类,每个点双对置换个数和置换贡献都是独立的,有如下观察:
- 若点双只有两个点,置换只有 \(1\) 个,贡献和为 \(k\)
- 若点双只有一个简单环构成(大小为 \(L\)),置换有 \(L\) 个,贡献为:\(\sum\limits_{i = 1} ^ L L ^ {(L, i)}\)
- 剩下的情况,可以猜测可以构成点双内边(记为 \(E\))的任意置换,那么置换有 \(E!\) 个,贡献为 \(\binom{E + k - 1}{k - 1}E!\)
前两点都是容易证明的,考虑证明第三点,即点双内存在环有边相交,不妨来试着任意两条边是否能在其他边不动的情况下交换。
首先注意到只有两个环相交的时候也满足观察三,那么我们只需要考虑保留两个这样的简单环即可。
此时我们发现,两个有边相交的简单环的三度点上的两条临边一定可以交换,交换方式如下图所示:
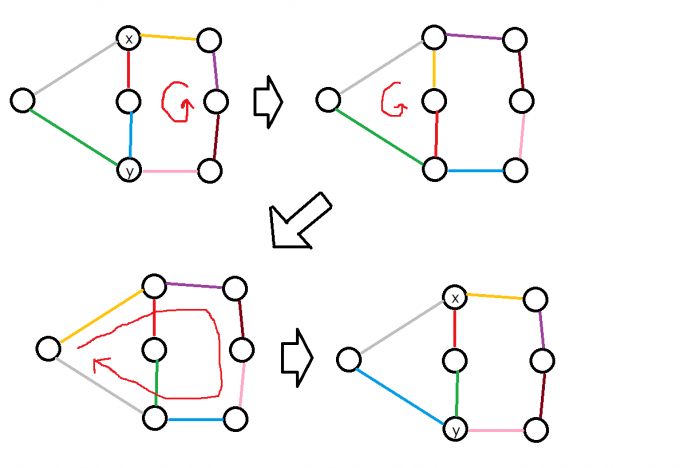
然后对与任意两条边,一定可以存在一种方式将两条边移动到这样三度点的两条邻边位置(不需要保证其他边不变),然后用上面的方法交换三度点的两条邻边,最后按照原来的顺序逆序操作即可交换任意两条边,这样原命题显然成立。
然后问题就变成了找每个点双内部的边数了,可以在求点双的过程当中维护每个点的当前度数,就只需要查询点双顶点和其他边之间的边数了,复杂度 \(\mathcal{O}(n)\).