定义
Stern-Brocot Tree 是一种人为构造生成 所有正有理数的树形结构,树上的每个节点与全体有理数(最简形式) 构成双射。
简单来说,这棵树是这样生成的:
首先由两个初始分数 \(\frac{0}{1}, \frac{1}{0}\)(后者虽然无定义但可视作 \(\infty\) 这只是形式化的辅助)构成序列 \(F_0\) 开始。
每一次迭代考虑在 \(F_i\) 任意两个相邻分数 \(\frac{a}{b}, \frac{c}{d}\) 之间插入一个分数:\(\frac{a + c}{b + d}\) 构成一个新的序列 \(F_{i + 1}\),如下图所示:

以 \(F_1\) 中的 \(\frac{1}{1}\) 为根,以与左边的数生成的数为左儿子,与右边生成的数作为右儿子(已经在树上出现过的节点不连左右儿子)为了方便构造,我们将数上出现过的数平移下放构成序列 \(F_{i + 1}\)(实际上这些数并不在 Stern-Brocot 树中),如下图所示:
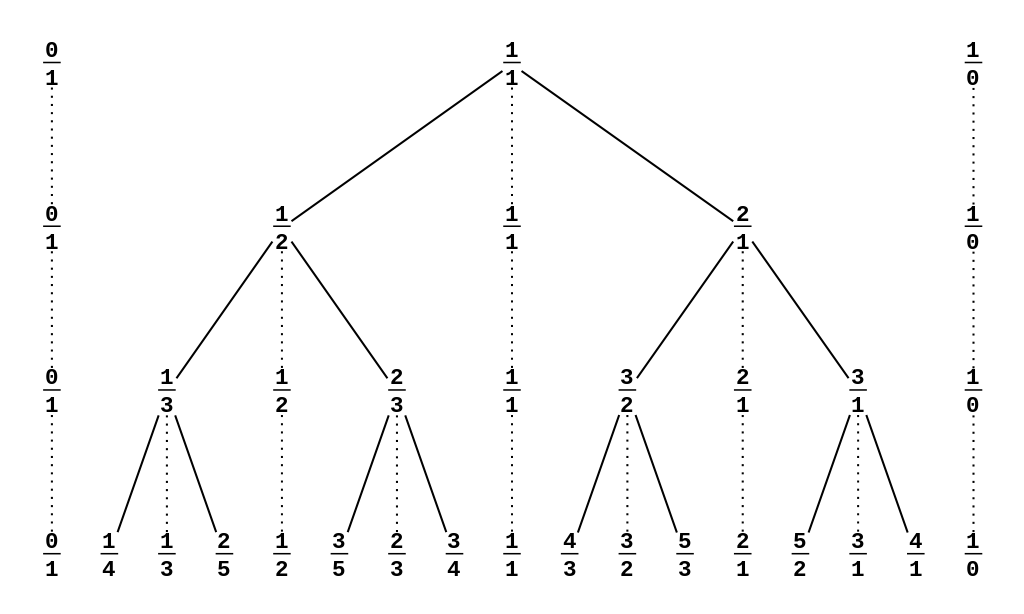
性质
性质 \(1\):\(\forall k > 0, F_k\) 中相邻三项 \(\frac{a}{b}, \frac{c}{d}, \frac{e}{f}\) 满足 \(c = a + e, d = b + f\)。
由定义。
性质 \(2\):SBT 深度不超过 \(k\) 的点构成的导出子树的中序遍历为序列 \(F_k\)
证明不难。
性质 \(3\)(单调性):\(\forall k, F_k\) 单调递增。
只需证:对于 \(F_{k - 1}\) 相邻的两个分数:\(\frac{a}{b}, \frac{c}{d}\) 满足 \(\frac{a}{b} \le \frac{a + c}{b + d} \le \frac{c}{d}\),做简单代数变换即可。
推论 \(1\):SBT 为一颗二叉搜索树。
性质 \(4\):\(\forall k, i \le 2 ^ {k - 1}, F_{k, i}, F_{k, i + 1}\) 两个分数 \(\frac{a}{b}, \frac{c}{d}\) 满足 \(bc - ad = 1\)。
归纳易得(本性质由性质二的证明不难发现)。
性质 \(5\):SBT 的每个节点均为最简分数。
由性质三与裴蜀定理容易得到:\(a, b, c, d\) 两两互质,显然可以得到该结论。
性质 \(6\)(折半性):称从 SBT 上任意一个节点 \(\frac{a}{b}\) 沿着相同方向跳到需要换方向的第一个点为一次跳跃,那么该点到根节点至多跳跃 \(\mathcal{O}(\log \max(a, b))\) 次。
令当前链顶为:\(\frac{p_1}{q_1}\) 链顶父亲为 \(\frac{p_2}{q_2}\),链顶父亲的父亲为 \(\frac{p_3}{q_3}\)。
那么有:\(p_1 = p_2 + p_3 \ge 2p_3, q_1 = q_2 + q_3 \ge 2q_3\),那么每次跳链 \(a, b\) 至少减半。
因为 SBT 结构巨大,因此该性质常用于 不建出树 情况下加速跳链过程。
性质 \(7\)(唯一性):SBT 上每个节点对应的有理数两两不同。
容易发现 \(\forall k > 0, F_k\) 内的数两两不同,归纳易证。
性质 \(8\)(覆盖性):任意的正有理数(最简形式)都必定会在 SBT 上出现。
只需证 \(\forall p, q > 0, (p, q) = 1, \frac{p}{q}\) 会在有限次迭代后在 \(F\) 中出现即可。
注意到 \(F\) 迭代的过程就是逐渐逼近有理数的过程,于是我们来考虑它是如何逼近的。
一开始显然有上下界:\(\frac{a = 0}{b = 1} < \frac{p}{q} < \frac{c = 1}{d = 0}\),然后随着 \(F\) 的迭代,我们发现:
-
若 \(p = a + c, q = b + d\) 那么此时 \(\frac{p}{q}\) 在 SBT 上出现。
-
否则一定能得到一个更紧的界:\(\frac{a}{b} < \frac{p}{q} < \frac{a + c}{b + d}\) 或 \(\frac{a + c}{b + d} < \frac{p}{q} < \frac{c}{d}\)
观察界的性质有:\(\frac{p}{q} - \frac{a}{b} > 0, \frac{p}{q} - \frac{c}{d} < 0 \Longleftrightarrow pb - aq \ge 1, cq - pd \ge 1\)。
考虑构造不等式:\((pb - aq)(a + b) + (cq - pd)(c + d) \ge a + b + c + d\)
也即 \(\frac{a}{b}, \frac{c}{d}\) 得到的中分位数 \(\frac{m}{n}\) 满足:\((pb - aq)(a + b) + (cq - pd)(c + d) \ge m + n\)
利用性质 \(3\) 简单化简得:\(p + q \ge m + n\) 因为 \(p + q\) 有限,\(m, n\) 每次必然增大因此经过有限次数后必为情况 \(1\) 也即 \(\frac{p}{q}\) 在序列上出现。
推论 \(2\):SBT 与全体正有理数(最简形式)构成双射,也即 SBT 是一个 表示正有理数的数系。
矩阵表示法
容易发现任意正有理数与 SBT 从根开始往下走的一条路径构成双射,也即和一个 \(01\) 序列(\(0\) 往左儿子,\(1\) 往右儿子)构成双射。
不难意识到两个问题:给定 \(01\) 序列如何快速求出其对应的有理数?给定一个有理数如何快速求出其对应的 \(01\) 序列?
问题 \(1\)
注意到 SBT 本质上就是在逼近所有有理数,知道当前的界和缩放方向就能得到下一次的界,知道缩放结束此时上下界的中分位数即为答案。
将上下界 \(\frac{a}{b}, \frac{c}{d}\) 看作两个二元向量组 \((a, b), (c, d)\) 容易发现一次缩放就是两个二元组之间的线性变换。
因此考虑将上下界用一个 \(2 \times 2\) 的矩阵表示:\(\begin{bmatrix} a & c\\ b & d\end{bmatrix}\)
往左儿子走等价于右乘:\(M_0 = \begin{bmatrix} 1 & 1\\0 & 1\end{bmatrix}\)
同理往右儿子走等价于右乘:\(M_1 = \begin{bmatrix} 1 & 0\\1 & 1\end{bmatrix}\)
如果直接暴力利用矩乘模拟树上往下走的过程,复杂度与暴力无异。
由性质 \(6\),不妨将 \(01\) 序列中极长的 \(01\) 缩起来(条件是 \(01\) 序列非给定而是隐式的)这部分矩乘用倍增加速,复杂度降为 \(\mathcal{O}(\log \max(a, b) \times \log |S|)\)。
问题 \(2\)
同样将 \(01\) 序列用线性变换来表示,由推论 \(1\) 可知我们可以通过分数大小比较确定任意一个分数 \(\frac{a}{b}\) 在 SBT 上的位置。
朴素做上界是 \(\mathcal{O}(\max(a, b))\) 的,考虑加速这个过程。
类似问题 \(1\) 中最后加速的方式,我们倍增跳右链的过程,倍增到第一个不能往右跳的位置。
预处理\(M_0, M_1\) 在 \(2\) 的次幂下的结果,复杂度 \(\mathcal{O}(\log ^ 2\max(a, b))\)。