关于最短路,大家应该都知道有Dijkstra,SPFA以及Floyd。
此处先提出一个问题:
给定图G,每条边有边权。
求从一点到另一点的边权和最小的路径。
要求图中不能有负回路(否则为NP问题)。
首先提到的便是Floyd。
如果数据范围足够小,相信大家大部分会选择Floyd(为什么呢,后文解释)。
大家都知道Floyd板子好背,不像其它两种算法一样颇为复杂。
但别看它貌似简单,但其实蕴含着大道理,这也是我去清北学堂的时候听hzc老师讲的。
Floyd的储存方法就是用邻接矩阵储存,比较方便。
它的原理是DP,时间复杂度为O(n3),空间复杂度为O(n2)。
所以Floyd是不可以用来做数据范围较大的题的。
令f[i][j][k]为从i到j,中途只经过编号1~k的节点的最短路。
考虑是否经过k:
如果经过,那么f[i][j][k]=f[i][k][k-1]+f[k][j][k-1];
否则,f[i][j][k]=f[i][j][k-1];
直接这样做的空间复杂度是O(n3),我们可以进一步优化。
首先,f[..][..][k]只从f[..][..][k]转移,可以用滚动数组优化。
进一步地,如果经过k,那么只会从fp..[[k][k-1]转移,而f[k][..][k]和f[..][k][k]必然不会这样转移,故可以直接在原数组上迭代。
代码实现:

f[i][j]的初始值需设为极大值,如果i与j之间有边那么f[i][j]为最小的边权。
拓展应用:
求图中的最小环。先考虑无向图。
Floyd算法保证了最外层循环到|的时候所有点对之间的最短路只经过1 ∼k− 1号节点。
环至少有3个节点,设编号最大的为x,与之直接相连的两个节点为u和v。
环的长度应为f[u][v][x-1]+w[v][x]+w[x][u]。其中w为边权,如不存在边则为无穷大。
我们只要进行第x次迭代之前枚举所有编号小于k的点对更新答案即可。
代码实现:
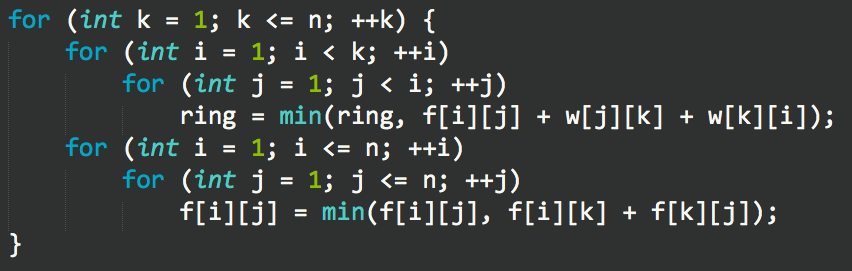
j只循环到i-1,因为无向图i到j与j到i是等价的。
有向图则类似,另外注意两个点的环的情况。
接下来我们来看SPFA(Shortest Path Faster Algorithm)
即队列优化的Bellman-Ford算法,同样用于求单源最短路,可以用于带负权的图。
SPFA算法:
算法流程大致如下:
1.记S为起点,置ds=0;对于其它点x,置dx=∞;
2.维护一个队列,初始为空;加入S;
3.取出队首节点,记为u;
4.枚举所有与u相邻的节点v,用du+w(u,v)更新dv;如果dv被更新且v不在队列中,则将其加入队列;
5.如果队列不为空,返回3;否则算法结束。
代码实现
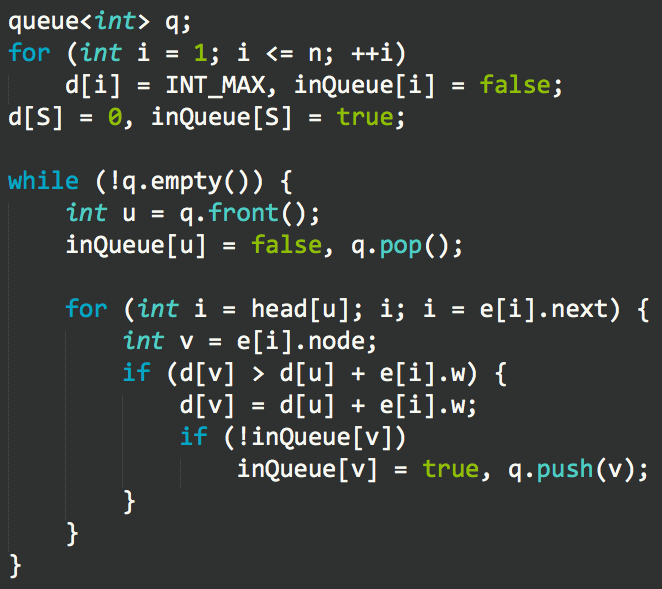
算法复杂度最坏情况下是O(nm)。
但一般来说,除非是故意卡SPFA,否则在效率上是和Dijkstra差不多的。

关于SPFA的优化:
1.SLF(smallest label first):如果加入的元素距离小于队首元素,则置于队首;
2.LLL(largest label last):记录队列中的元素距离平均值,从队首取元素时,如果距离大于平均值则移至队尾,重复直到找到小于等于平均值的元素为止;
3.随机化:从队首取元素时,有p的概率直接将其移至队尾;p应当是于图规模有关的一个小概率。
其实这些优化不能优化复杂度,甚至可能使算法变慢,但能在一定程度上化解针对性数据。
既然上文提到了Dijkstra,那么我们接下来自然要讲它。
首先我们来想一下宽度优先搜索
如果所有边权均为1,宽度优先搜索可以求出最短路。
如果不为1?则拆点。
用于求从图中一点出发到其它所有点的最短路。即SSSP(single source
shortest path,单源最短路)。
时间复杂度O(n2 ),空间复杂度O(m)(不含图结构)。
要求所有权值非负。称这样的图为正权图。
在下面的分析中,视1号点为源点,记du为1号点到点u的最短路距离。
我们首先来看一些正权图的性质:
1. 如果1到u的最短路上包含v,那么这条路径上1到v的部分为1到v的最短路。
2. 任意一条最短路的一部分的长度一定不大于整条路径的长度。

Dijkstra算法
算法流程大致如下:
1. 记S为起点,置ds = 0;对于其它点x,置dx = ∞;
2. 找到当前尚未处理过的点中距离最小的,记为u;
3. 枚举所有与u相邻的节点v,用du + w(u,v)更新dv ;
4. 标记u为已处理;
5. 如果还有尚未处理过的点,返回2;否则算法结束。
代码实现:

关于优化:
首先改变储存图的方式;
再者,我们考虑优化循环,外层循环无法优化,则内层为先找最小值,更新答案。
我们使用堆优化。
堆是一个支持插入元素、查询或删除最小值的数据结构。
插入、删除复杂度为O(log n) ;
查询复杂度为O(1) ;
还可以支持把一个元素改小,复杂度为O(log n)。
不需要明白具体实现,当成一个黑箱就好。

为了优化查询最小值部分,我们需要存储所有尚未处理过的点。
在更新时候,如果距离变小,则在堆中更新。
而在更新时,也只在前向星中遍历从当前点发出的边。
复杂度O(nlog n)。
另一种写法是直接往堆里加,而不是改值,适用于STL中的优先队列。
就不再具体实现了。
我在冬尽外,祈你沐艳阳。