前言:
本文参考《信息学奥赛一本通·金牌导航》。
正文:
Manacher 算法:
Manacher 算法,经常被称作马拉车,可以以 (mathcal{O}(n)) 的时间复杂度求出字符串关于回文子串一类的问题。
介绍:
首先举个例子,设字符串 (s= exttt{bbdkd})。
在这里面,有偶回文子串 ( exttt{bb})、奇回文子串 ( exttt{dkd}),在计算的过程中还要对奇偶问题进行讨论太过于麻烦,所以可以在每个字符之间加入特殊字符(首尾特殊字符可以作边界):
再设 (R_i) 表示以第 (i) 位字符为中心的最长回文的半径。对应上面的 (s') 可以得到:
可以发现,以 (i) 为中心的最长回文子串长度就是 (R_i-1)。
我们在求解 (R) 数组的过程中再设 (p,mx) 分别表示当前回文子串中心和回文子串的右端点。若正在计算 (R_i),令 (i) 关于 (p) 的对称点 (j=2p-i)。然后为了先给 (R_i) 定下界,进行分类讨论(结合图片思考):
- (mxleq i),因为恒有 (R_igeq 1),所以 (R_i) 下界是 (1)。
- (mx-i>R_j),(j) 的左端点没有包裹住 (p) 的左端点(即以 (j) 为中心的回文子串被包含与 (p) 的)。因为是对称点,所以以 (i) 为中心的回文子串也一定被包含与 (p) 的,所以 (R_i) 下界为 (R_j)。
- (mx-ileq R_j),(j) 的左端点包裹住了 (p) 的左端点(即以 (j) 为中心的回文子串不被包含与 (p) 的)。因为不被包含,所以不能保证在 (mx') 以前的字符和 (i) 的对应,所以下界是 (mx-i)。
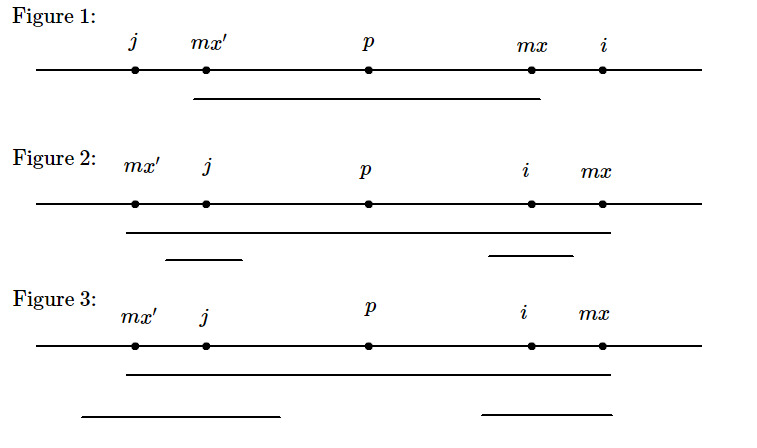
简单来说,定下界就是取 (min(mx-i,R_j))。
定完下界后,再往两边枚举检测一遍。
由于向左右拓展成功必然会导致 (mx) 向右移,而 (mx) 向右移不超过 (n) 次,故向左右拓展操作的总时间复杂度是 (mathcal{O}(n))。枚举 (i) 也是(mathcal{O}(n)) 的,那么 Manacher 算法时间复杂度是 (mathcal{O}(n))。
代码:
int p = 1, mx = 1;
for (int i = 1; i <= n; i++)
{
R[i] = min (mx - i, R[2 * p - i]);
while (s[i - R[i]] == s[i + R[i]]) ++R[i];
if (i + a[i] > mx)
mx = i + R[i], p = i;
}
例题:
后缀数组:
介绍:
注意:本文第 (i) 个后缀是指关于原字符串 (S) 的子串 (S_{icdots ext{len}})。
后缀数组 (SA) 就是以此存储将 (s) 的 (n) 个后缀从小到大排序后的数组。即:排名为 (i) 的后缀是哪一个。
名次数组 (Rank) 和 (SA) 的互逆,它储存的是第 (i) 个后缀的排名。
求出后缀数组 (SA),一般使用倍增的方法:用倍增对每个字符开始的长度 (2^k) 的子字符串进行排序,得到 (Rank)。(k) 从 (0) 开始,每次加一,当 (2^k) 大于 (n) 就一定能比较出大小。每次排序利用上一次长度为 (2^{k-1}) 的两个字符串排名作为两个部分,然后基数排序,就能得到长度为 (2^k) 的字符串的排名。如图举例子:

其中 (x,y) 就分别是前半部分和后半部分。这两个部分正好在基数排序中看作是两位。然后假设后半部分已经有序,而且前半部分排名相同的必然在倍增后排名依然为连续一段,所以我们可以求出前半部分每个排名倍增后所在的区间。接着,倒序枚举后半部分,并依次在所在区间末尾插入即可。
也可以从上图得知倍增是 (i) 的前半部分其实就是倍增前 (i) 的排名,其后半部分就是就是将要合并的第二部分的起始位置。
还有一点:
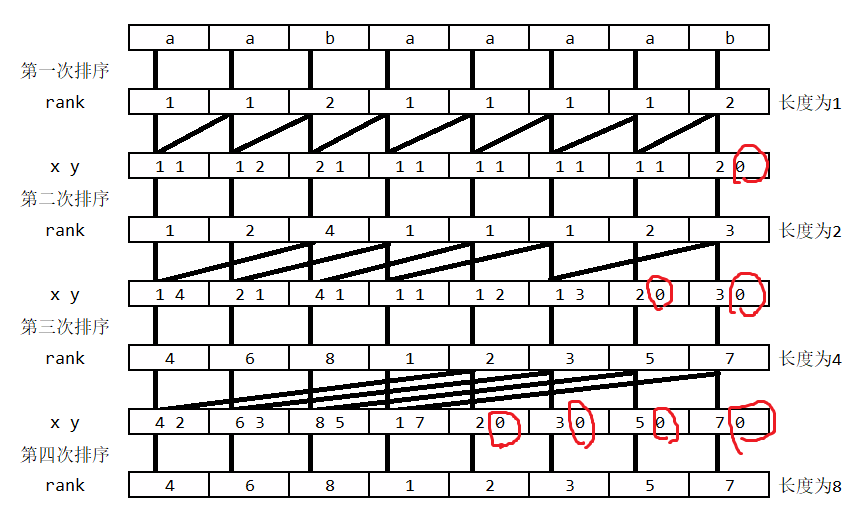
如图红圈,有的位置在合并过程中已经没有了后半部分,我们把它当作是该前半部分最小的,这里有点难理解,由于两个部分在基数排序中看作是两位数,换句话说这里的意思就是个位当作是 (0),就成了该十位中最小的数。
代码:
int n, m;
int sa[N], c[N], x[N], y[N];
char s[N];
void Solve()
{
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i] = s[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[i]]--] = i;
for (int k = 1; k <= n; k <<= 1)
{
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //The numer has no the latter part
for (int i = 1; i <= n; i++)
if(sa[i] > k) y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]]++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]]--] = y[i], y[i] = 0;
swap(x, y);
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k])? num: ++num;
m = num;
if (n == m) break;
}
return ;
}
int main()
{
// freopen(".in", "r", stdin);
// freopen(".out", "w", stdout);
scanf ("%s", s + 1);
n = strlen(s + 1), m = 122;
Solve();
for (int i = 1; i <= n; i++)
printf ("%d ", sa[i]);
return 0;
}