第三章--网络基本拓扑性质(复杂网络学习笔记)
节点的度和平均度
- 度: (节点i的度k指的是与节点i直接相连的边的个数)
- 出度: 节点(i)指向其他节点的边数
- 入度: 其他节点指向节点(i)的边数
- 平均度: 网络中所有节点的度的平均值
- (k_i): 节点i的度
- (<k>): 网络的平均度

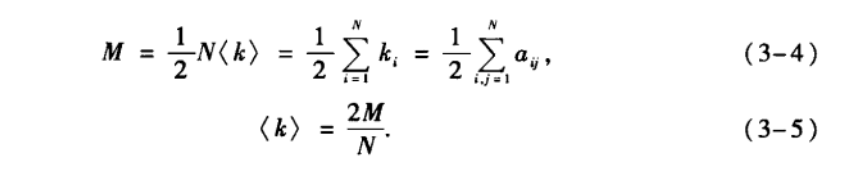
如果是加权网络G, 那么节点的度经过加权可以定义为出强度和入强度
网络稀疏性和稠密化
- 网络的密度: 一个包含(N)个节点的网络的密度( ho)定义为网络中实际存在的边数(M)与最大可能的边数之比,即
[
ho=frac{M}{frac{1}{2}N(N-1)}
]
对于有向网路, 上式中的1/2去掉即可.
如果当N趋于无穷大并且网络密度是一个常数,则表明实际是网络边数与(N^2)是同阶的, 那么则说该网络是稠密的.
- 平均度: (<k>=frac{2M}{N})
- 密度 : ( ho = frac{M}{frac{1}{2}N(N-1)})
- 平均度和密度的关系: (<k>=(N-1) ho approx N ho)
平均路径长度和直径
平均路径长度
- 最短路径: 网络中两个节点之间的
边数最少的路径称为最短路径 - 距离(d_{ij}): 定义为节点i,j的最短路径的边数.
- 平均路径长度(L): 定义为网络中任意两个节点距离的平均值
[L=frac{1}{frac{1}{2}N(N-1)}sum_{i>=j}d_{ij}
]

网络直径
- 网络直径D: 定义为网络中任意两个节点距离的最大值
[D=max(d_{ij})
]
实际上,我们可能更关心的是网络中绝大部分用户对之间的距离,因此先给出以下定义:
- (f(d)): 统计网络中距离
等于(d)的连通的节点对占整个网络中连通的节点对的比例 - (g(d)): 统计网络中距离
不超过(d)的连通的节点对占整个网络中连通的节点对的比例
一般的, 如果直径(D)满足
[g(D-1)<0.9, g(D)ge0.9
]
那么就称D为该网络的有效直径.
最短路径算法
- Dijkstra算法: 一般用于求加权有向网路(权值为非负)中的节点之间最短路径
- bellman-ford算法: 用于存在权值为负的情况
聚类系数(clustering coefficient)
- 某个节点的
聚类系数刻画了该节点的邻居节点中任意一对节点,有连边的概率.
[C_i=某个点的聚类系数=frac{该点的邻居节点之间实际存在的边数}{这些邻居节点可能存在的最大的边数}
]
[C_i=frac{E_i}{k_i(k_i-1)/2}=frac{2E_i}{k_i(k_i-1)}
]
其中
- (E_i) : 该点的邻居节点之间实际存在的边数
- $ k_i(k_i-1)/2$ : 这些邻居节点可能存在的最大的边数
度分布(degree distribution)
有连接才会有网络, 我们自然关心网络中节点的度的分布情况.
高斯分布(正太分布/钟型分布)
正太分布是针对连续性随机变量而言, 其对应的离散型随机变量,最常见的是泊松分布(poisson distribution)
[P(k)=frac{lambda^ke^{-lambda}}{k!}
]
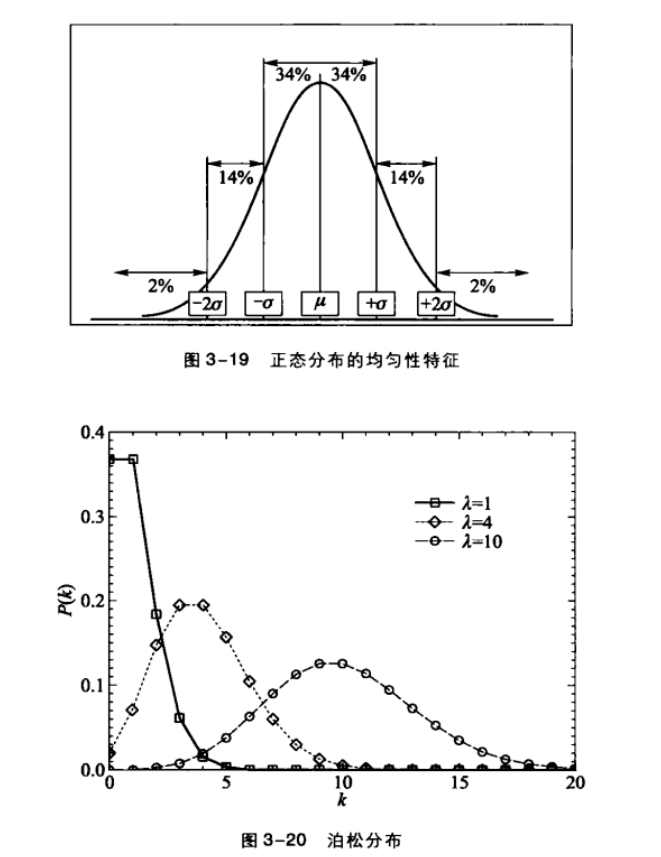
幂律分布(长尾分布/无标度分布)



幂律分布及其检验, 性质
用时再查阅资料.