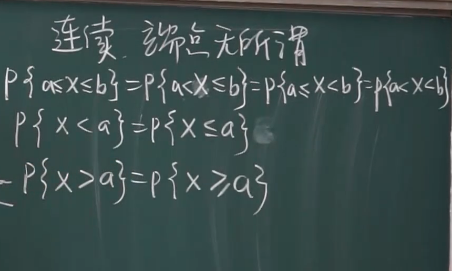随机变量的概念
概念: 随机变量是表示随机现象各种结果的变量。如硬币正反面为1,0.那么1,0即为随机变量.
定义 : 有样本空间(Omega),并且(omega in Omega), (X=X(omega))是一个实值函数,则称X为样本空间中的随机变量,即把样本空间映射到一个实数集上.
记号: 一个事件可表示({X=a}) , 事件的概率可表示为:(P(X=a),P{X=a})
离散型随机变量
概念: 离散型随机变量(X)的取值必须的可列的,如(x_k(k=1,2,3....n))
- (X): 表示变量
- (x): 具体的取值.
概率分布(函数)
(P{X=x_k}=p_k) : 叫概率函数/分布 , 满足条件(P_kgeq0,sum p_k=1)
连续性随机变量
- 离散型 -> 概率函数
- 连续性 -> 概率函数(又叫概率密度函数)
- 概率密度函数和概率分布函数的积分(面积)为1.
概率密度函数: 有非负可积函数(f(x), f(x)geq 0, aleq b, 如果p{a<Xleq b}=int_a^bf(x)), 则称(f(x))为连续随机变量(X)的概率密度函数.
概率密度函数两个性质:
- (f(x)geq 0)
- (int_{-infty}^{+infty}f(x)=1)
- 连续变量取个别值的时候,概率为0
注:
- 连续型随机变量的区间,包含不包含端点无所谓