无向图的双连通分量

概念解释

连通分量：无向图的极大连通子图。连通图的连通分量是其自身，非连通图有多个连通分量
割边(桥)：一无向图中，一条边称为桥应当满足当删除这条边后，图的连通分量增多
割点：一无向图中，一个点称为割点应当满足当删除这个顶点和与其相关联的边后，图的连通分量增多
边双连通分量：一连通分量称之为边连通分量，应当满足去掉任意一条边，都不会改变此图的连通性，即不存在桥
点双连通分量：一连通分量称之为点连通分量，应当满足去掉任意一个点后，都不会改变此图的连通性，即不存在割点

[易错点]

两个割点之间的边不一定是桥
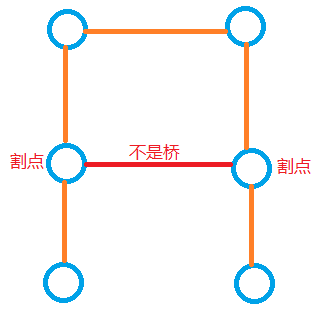
桥的两端点不一定是割点
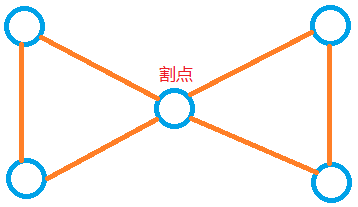
点双连通分量不一定是边双连通分量

[注]：一个点显然是连通的
边双连通分量不一定是点双连通分量

桥的判定及求解e-Dcc实现思路

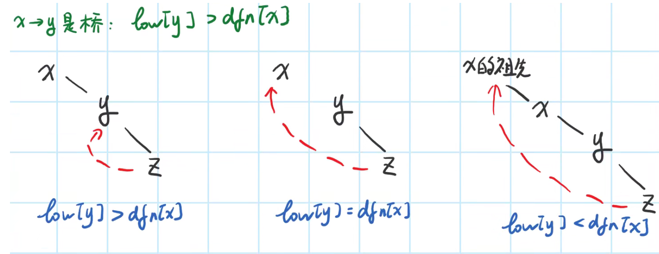
与有向图求scc类似，同样引入(dfn)和(low)两个标记。对于(x, y)，如果x->y是桥，应当满足(low[y] > dfn[x])

易错点

此时为无向图，同时存在父->子，子->父两条路径，在Tarjan过程中，必须保证一条边不能重复走，因为桥的判定条件为(low[y] > dfn[x])，如果可以重复走，则至少可以满足(low[y] >= dfn[x])，无法再判定出桥的存在了
在有向图中，存在一种情况是，“一个点a处在某个scc中，另一个点b搜索到a点时a已经弹栈”，出现这种情况说明b点不会处在a所在的scc中，用a点数据更新b点是错误的，因此需要加入in_stk的判断。但是在无向图中，假设存在一种情况是“一个点a处在某个e-dcc中，另一个点b搜索到a点时a已经弹栈”，由此构造出下图，由于是无向边，在b搜索到a之前a已经将b搜索过了，同时边双连通分量过程是不允许一条边走两次的，因此b走到a的路径是非法路径(这是因为无向图中不存在横叉边)，也就是说上述假设情况是无法发生的，因此在搜索到一个已经被搜索过的点时，无需判断其是否处在栈中

代码实现

/**
 * u: 待搜索点编号
 * from: 来到u点的边编号，用于保证一条边仅走父->子，不走子->父
 * eDcc_cnt：边双连通分量编号
 * is_bridge[i]：标记编号为i的边是否为桥
 * id[i]：标记编号为i的点处与的边双连通分量编号
 * 说明：代码中异或的运用，在无向图加边时，0和1代表同一条边，2和3代表同一条边，而0^1=1，1^1=0，2^1=3，3^1=2，借此判断是否走的是来时的路
 */
void tarjan(int u, int from)
{
    dfn[u] = low[u] = ++ timestamp;
    stk.push(u);

    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if (dfn[u] < low[j]) 
                is_bridge[i] = is_bridge[i ^ 1] = true;
        }
        else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]);
    }

    if (dfn[u] == low[u])
    {
        int y;
        ++ eDcc_cnt;
        do {
            y = stk.top(); stk.pop();
            id[y] = eDcc_cnt;
        } while (y != u);
    }
}

割点判定及求解v-Dcc实现思路

割点的判定同样利用(dfn)和(low)两个标记，对于点x，其是割点有以下情况

x不是根节点(root) && x有儿子y && (low[y] >= dfn[x])
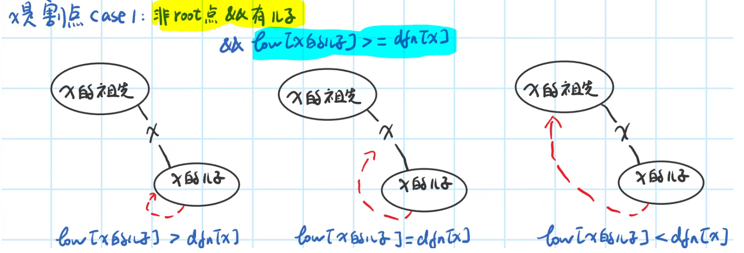
x是根节点 && 在深度搜索树中x有2个以上的儿子

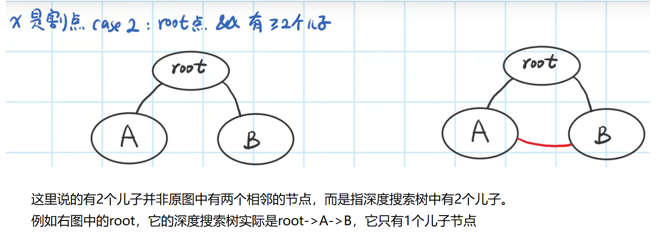
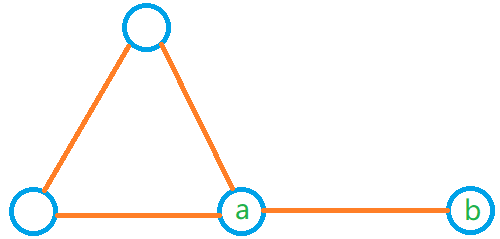
注：情况2中给定的条件是“在深度搜索树中有2个以上儿子”，这不同于在图上x有2个以上儿子，例如右图，根节点的确有2个儿子A和B，但A和B之间的连接使得root节点并非割点

易错点

不需要一条边不能重复走的判断，割点的判断条件为(low[y] geq dfn[x])，一条边重复走导致的结果是 (low[y] = dfn[x])，这并不会影响割点的判断
不需要in_stk的判断，理由同桥的判断

代码实现

/**
 * 函数功能：将一非连通图转化为各个点双连通分量
 * root：枚举的根节点
 * isCut[i]：标记点i是否为割点
 * vDcc[i]：编号为i的点双连通分量(点的集合)
 * 
 * 注：在划分点双连通分量时，我们将割点划分到其所属的每一个点双连通分量
 */
void tarjan(int u)
{
    dfn[u] = low[u] = ++ timestamp;
    stk.push(u);

    // 特判孤立点，每一个孤立点都是一个单独的点双连通分量
    if (u == root && h[u] == -1) // u == root 和 h[u] == -1是等价的，这里为了代码可读性全部写上了
    {
        ++ vDcc_cnt;
        vDcc[vDcc_cnt].push_back(u);
        return ;
    }
    
    int cnt = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (low[j] >= dfn[u]) // 仅这一个条件只能判断出j及栈中节点构成一个v-DCC，u是不是割点不能确定
            {
                /**
                 * 满足low[j] >= dfn[u]的前提下，总共有3种情况
                 * 1. u不是根节点
                 * 2. u是根节点但其下有<=1个v-Dcc
                 * 3. u是根节点但其下有>1(>=2)个v-Dcc
                 * u点是割点有两种情况：
                 * 1. u不是根节点 (u != root)
                 * 2. u是根节点但是u下有至少2个v-DCC (cnt > 1)
                 */
                ++ cnt; // cnt每次自增都代表着u节点下存在着一个v-Dcc
                if (u != root || cnt > 1) isCut[u] = true; 
                int y;
                ++ vDcc_cnt;
                do {
                    y = stk.top(); stk.pop();
                    vDcc[vDcc_cnt].push_back(y);
                } while (y != j);
                vDcc[vDcc_cnt].push_back(u); // 不能放到do-while中是因为一个割点可能属于多个vDcc，不能只存储一次
            }
        }
        else low[u] = min(low[u], dfn[j]);
    }
}